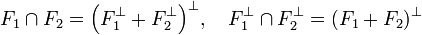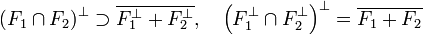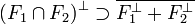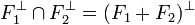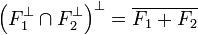- Orthogonal
-
Orthogonalité
 L'équation régissant la propagation de la chaleur se résout à l'aide de l'orthogonalité dans un espace de dimension infinie.
L'équation régissant la propagation de la chaleur se résout à l'aide de l'orthogonalité dans un espace de dimension infinie.
En mathématiques, l'orthogonalité est un concept d'algèbre linéaire associé à une forme bilinéaire. Un cas fréquent est celui où cette forme est un produit scalaire.
Si un espace est munie d'une géométrie euclidienne, il est naturellement équipé d'une distance, deux vecteurs sont orthogonaux si et seulement si leurs directions sont perpendiculaires ou encore forment un angle droit. Depuis la Grèce antique, l'angle droit est à l'origine de la démonstration de nombreux théorèmes. Ceux de Pythagore et de la médiane sont des exemples. Les grands et petits axes d'une ellipse sont orthogonaux, source de multiple propriétés.
L'orthogonalité généralise dans un premier temps l'idée d'angle droit à un espace de dimension finie muni d'un produit scalaire. Les résultats découverts dans l'univers précédent prennent une nouvelle forme. Les axes principaux d'une surface quadrique sont orthogonaux, cette propriété permet leur classification. L'article théorème spectral montre de nombreuses applications, comme la résolution de l'équation du mouvement d'une corde vibrante modélisée par des petites masses en nombre fini et à égales distance ou la méthode des moindres carrés en statistiques.
L'orthogonalité s'applique encore si les nombres sous-jacents ne sont plus réels. L'usage des nombres complexes amène à une autre géométrie, dite hermitienne. En arithmétique, l'utilisation de l'orthogonalité sur les nombres entiers permet à Joseph-Louis Lagrange (1736-1813) de trouver une nouvelle démonstration du théorème des deux carrés de Fermat. Les représentations d'un groupe fini font appel à des ensembles de nombres finis. L'orthogonalité y joue un grand rôle.
L'analyse fonctionnelle n'est pas en reste. Il est parfois possible de définir un produit scalaire sur un espace de fonctions à valeurs réelles ou complexes de dimension infinie. L'orthogonalité y est utilisée à travers la notion de base de Hilbert, une généralisation de la base orthonormale. Elle permet de résoudre des équations comme celle de la chaleur ou d'une corde vibrante dans le cas général. Parfois, l'espace de fonctions ne dispose pas de produit scalaire. Le dual topologique permet alors de faire usage de l'orthogonalité. Le crochet de dualité est une forme bilinéaire qui s'applique sur le dual et et l'espace, il remplace le produit scalaire et permet d'obtenir des résultats un peu analogues aux configurations précédentes.
Sommaire
Géométrie d'Euclide
Définitions
Une première approche intuitive associe l'orthogonalité à l'angle droit. Dans ce paragraphe E est plan équipé d'une géométrie euclidienne, comme l'angle droit est défini à l'aide de deux droites, et que deux droites sont toujours coplanaires, il n'est pas utile d'aller plus loin. En revanche les résultats s'appliquent encore dans notre espace usuel de dimension trois. Le plan est formalisé soit par les cinq postulats d'Euclide[1], soit pour être parfaitement rigoureux par les vingt axiomes de Hilbert[2]. E possède des transformations particulières, de E dans lui-même, appelées isométries. Elles conservent les distances. Ainsi, si A et B sont deux points de E et ψ une isométrie, la distance entre ψ(A) et ψ(B) est la même que celle entre A et B. Dans un tel espace, les isométries sont les translations, les rotations et les réflexions correspondant à l'image d'un miroir.
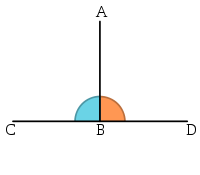
Définition 1 — Deux droites sécantes et non confondues Δ1 et Δ2 forment un angle droit, ou encore sont orthogonales si et seulement s'il existe une rotation tel que l'image de Δ1 (resp. Δ2) soit Δ2 (resp. Δ1).
La seule rotation utilisable pour cette définition est celle d'un quart de tour. Il serait possible de définir l'angle droit à l'aide d'une réflexion. Les droites Δ1 et Δ2 sont perpendiculaires si et seulement s'il existe une réflexion d'axe Δ1 laisse globalement invariant Δ2.
Il est aisé de remarquer que si une droite Δ2 est perpendiculaire à une droite Δ1 et si Δ2 est parallèle à une droite Δ3, alors les droites Δ1 et Δ3 forment un angle droit. La notion d'orthogonalité ne s'applique pas seulement à des droites mais, de manière plus générale à des directions. Deux droites sont dites avoir même direction si et seulement si elles sont parallèles.
Définition 2 — Deux directions δ1 et δ2 sont orthogonales, ou encore forment un angle droit, si et seulement s'il existe une droite Δ1 (resp. Δ2) de direction δ1 (resp. δ2) tel que Δ1 et Δ2 soient perpendiculaires.
Ces deux définitions permettent de nombreuses généralisations. Ainsi deux segments (resp. vecteurs) (resp. bipoints) sont orthogonaux si et seulement si leurs directions le sont. Une droite Δ est perpendiculaire à un plan si et seulement si toute droite du plan est orthogonale à Δ.
Propriétés
Pour la géométrie du triangle, la tradition consiste à utiliser le terme de perpendiculaire et non orthogonal, dans ce contexte, les deux notions sont rigoureusement équivalentes.
La propriété fondamentale de la géométrie d'Euclide est le théorème de Pythagore. Il s'exprime ainsi :
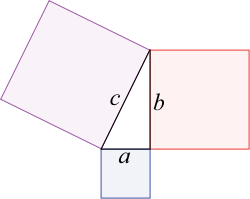
Théorème de Pythagore — Dans un triangle rectangle, le carré de la longueur de l'hypoténuse (côté opposé à l'angle droit) est égal à la somme des carrés des longueurs des côtés de l'angle droit.
Ce résultat semble être l'un des tous premiers théorèmes connus de l'humanité. On en trouve probablement des traces à une période datant d'avant l'écriture[3]. La première démonstration connue provient d'Euclide qui vivait autour de -300 av. J.C., elle est rédigée dans un texte nommé les Éléments.
La réciproque est aussi vraie. C'est-à-dire que si, avec les notations de la figure, la somme de l'aire des carré de coté a et b est égal à l'aire du carré de coté c, alors le triangle est rectangle. Autrement dit, si A, B et C sont trois points d'un plan, l'angle formé par les segments [A, B] et [A, C] est droit si et seulement si :
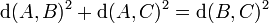
Dans cet article d(A, B) désigne la distance entre A et B.
Cette propriété permet de démontrer le théorème de la médiane attribué à Apollonius de Perga[4]. Il stipule que si A, B et C sont trois points du plan et si I est le milieu du segment [B, C] alors :
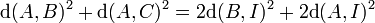
Le terme de médiane désigne une droite passant par un sommet et le milieu du coté opposé d'un triangle. Si un triangle A, B, C est tel que la distance entre A et B est la même que celle entre B et C, le triangle est dit isocèle. Soit I le milieu de A et C, alors le théorème de la médiane indique que :
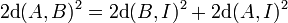
La condition nécessaire et suffisante précédente indiquant qu'un angle est rectangle est remplie et l'angle AIB est droit. Ceci démontre que les deux diagonales d'un losange sont perpendiculaires.
Constructions à la règle et au compas
Une première question consiste à savoir comment, à l'aide d'une règle et d'un compas, dessiner deux droites perpendiculaires. Une technique simple consiste à choisir deux points A et B sur la première droite Δ1 et à dessiner deux cercles de même rayon ayant deux points d'intersections. La droite Δ1, passant par les deux points d'intersection, est perpendiculaire à la première. La figure est un losange, l'étude des propriétés du paragraphe précédent montre que les deux droites sont perpendiculaires.
La figure de droite montre qu'il est inutile que les deux cercles soit de même rayon. En effet, avec les notations de la figure, soit D le deuxième point d'intersection des deux cercles et O le milieu de C et D. Comme le triangle CAD est isocèle, la droite passant par A et O est perpendiculaire à celle passant par C et D. Un raisonnement analogue montre que la droite passant par B et O possède les mêmes propriétés, elles sont donc les mêmes directions et un point commun O, ce qui montre qu'elles sont confondues avec la droite Δ1.
Cette technique de construction d'un angle droit est ancienne. Elle date probablement de Œnopide de Chios[5], un mathématicien grec vivant cinq siècles avant J.C.
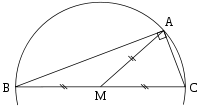
Une autre solution est illustrée par la figure de gauche. Elle consiste à tracer un cercle et un triangle dont un coté est un diamètre et dont le sommet est un point du cercle. Un tel triangle est toujours rectangle. En effet, le théorème de la médiane montre que la somme des carrés des longueurs des segments [A, B] et [A, C] est égal à quatre fois le carré du rayon, c'est-à-dire le carré de la distance entre B et C.
De nombreuses constructions à la règle et au compas utilisent les propriétés de l'orthogonalité. Elle permet de couper un angle en deux, à l'aide de la bissectrice. À l'exception du triangle équilatéral qui n'en a pas besoin, le dessin à la règle et au compas des polygones réguliers constructibles utilise les propriétés de l'orthogonalité.
Orthogonalité et théorèmes géométriques
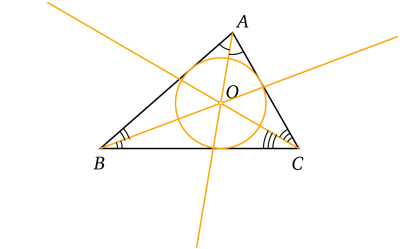 Bissectrices et cercle inscrit d'un triangle.
Bissectrices et cercle inscrit d'un triangle.De nombreux théorèmes géométriques utilisent le théorème de Pythagore et donc l'orthogonalité pour pouvoir être démontrés. Le fait que les trois bissectrices d'un triangles soient concourantes et soit le centre du cercle inscrit dans le triangles provient de la propriété d'orthogonalité de la bissectrice déjà rencontrée pour construire deux droites perpendiculaires.
De même, les trois hauteurs d'un triangle d'un triangles sont concourantes. Le point d'intersection s'appelle l'orthocentre. Une hauteur est une droite passant par un sommet et perpendiculaire au coté opposé. Un autre résultat précise que les trois médianes sont aussi concourantes. Le point d'intersection est le centre de gravité. Ce qui signifie que si un triangle est matérialisé en un solide homogène, il est en équilibre sur une pointe posée exactement sur ce point d'intersection. Leonhard Euler (1707 1783) trouve une droite remarquable. Le centre de gravité, le centre du cercle inscrit et l'orthocentre sont alignés. Cette droite est le centre d'un cercle étonnant appelé cercle d'Euler. Il passe par neuf points remarquables du triangle. Karl Wilhelm Feuerbach (1800 1834) établit son théorème affirmant que le cercle d'Euler est tangent aux trois cercles exinscrits du triangle. Tous ces théorèmes utilisent les propriétés de l'orthogonalité pour pouvoir être démontrées.
Utilisations dans d'autres contextes
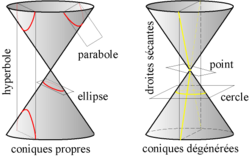
L'utilisation de l'orthogonalité en dehors de la géométrie date de la plus haute antiquité. Les babyloniens utilisent un triangle rectangle isocèle de coté un pour calculer la racine de deux. L'orthogonalité d'un angle ainsi que la formule de Héron leur permettaient d'accéder à une remarquable approximation[6]. Apollonius écrit un traité sur les coniques[7] qui fascinent de nombreuses générations[8]. Il y démontre les propriétés asymptotiques des hyperboles, des foyers et la base des propriétés des polaires réciproques[7].
L'antiquité n'est pas la seule période à utiliser des relations d'orthogonalité en géométrie. René Descartes (1596 1650) généralise l'idée d'abscisses et d'ordonnées déjà présente chez Apollonius[9] et utilise systématiquement l'angle droit pour définir ses repères[10], ce qui permet de calculer simplement la distance entre deux points dans le plan. Elle correspond à la somme des carrés des différences des coordonnées. Il utilise son repère pour établir les lois de l'optique[11] comme celles de la réfraction et de le reflexion.
Isaac Newton (1643 1727) utilise des propriétés d'orthogonalités (la traduction française utilise le mot perpendiculaire) pour établir les principes du calcul différentiel. Les définitions de dérivée et d'intégrale pour cet auteur se fonde sur des raisonnements géométriques où l'orthogonalité joue un rôle majeur. Newton les utilise pour déterminer la trajectoires des planètes autour du soleil[12]. Son formalisme correspond essentiellement à une logique analogue à celle d'Euclide, le recours au repère cartésien est rare.
Généralisation du concept
Arithmétique
 Un nombre premier est somme de deux carrés s'il se trouve sur un cercle dont le carré du rayon est entier. Cette remarque introduit l'orthogonalité dans l'arithmétique.
Un nombre premier est somme de deux carrés s'il se trouve sur un cercle dont le carré du rayon est entier. Cette remarque introduit l'orthogonalité dans l'arithmétique.
D'autres questions, bien éloignées de la géométrie du triangle sont finalement résolues avec l'orthogonalité. En 1640 Pierre de Fermat (1601-1665) se pose la question de savoir quels nombres premiers sont somme de deux carrés[13]. La question est d'apparence anodine, cinq et treize vérifient cette propriété, sept et onze non. Fermat devine juste en conjecturant que tout nombre premier impair dont le reste de la division par quatre est égal à un est somme de carré, mais comment le démontrer ? Plus d'un siècle et le talent d'Euler sont nécessaire pour en venir à bout[14]. L'équation x2 + y2 = p est enfin résolue, elle fait partie d'une interrogation plus vaste, dans quel cas l'équation x2 + n.y2 = p admet-elle une solution entière? De manière plus générale, dans quel cas l'équation suivante à coefficients entiers admet-elle une solution entière :
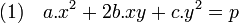
Une telle expression est appelée une forme quadratique. Lagrange propose une démarche originale, il remarque que, sous réserve de bonnes propriétés sur les coefficients a, b et c, la formule (1) représente le carré de la distance du point (x, y) à l'origine. La question est alors de savoir dans quel cas il existe deux vecteurs à coefficients entiers orthogonaux et de longueur un. Lagrange trouve la condition nécessaire et suffisante qui lui permet de conclure[15]. Ce raisonnement lui permet de résoudre l'équation x2 + n.y2 = p si n est égal à un, deux, trois, quatre ou cinq. Le cas général reste hors de portée. Il faut encore plus d'un siècle d'efforts et le talent de nombreux géomètres, souvent allemands pour en venir à bout[16]. L'arithmétique fait usage de l'orthogonalité, cependant, à la différence des grecs, les nombres associés ne sont plus les réels mais les entiers. La théorie voit un enrichissement à d'autres ensembles de nombres.
Dimension quelconque
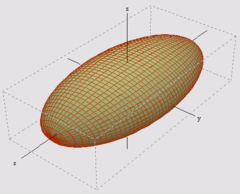 Comme toutes les quadriques, un ellipsoïde possède des axes principaux orthogonaux. Cette propriété permet leur classification.
Comme toutes les quadriques, un ellipsoïde possède des axes principaux orthogonaux. Cette propriété permet leur classification.
Une autre question impose une nouvelle généralisation. Depuis Newton, la trajectoire des planètes, essentiellement sous l'influence du soleil est relativement bien connue. Cependant, les planètes s'attirent entre elles, créant de petites perturbations par rapport à l'approximation de Newton, appelées variations séculaires. Lagrange cherche à démontrer que les variations du premier ordre ne peuvent déstabiliser le système[17]. Augustin Louis Cauchy (1789 1857) découvre que cette question est aussi associée à une forme quadratique. Il remarque qu'une équation de type (1) généralisée à la dimension trois définit une surface quadrique comme l'ellipsoïde de la figure de droite. Trouver les bons vecteurs orthogonaux pour cette quadrique lui permet de les classifier toutes[18]. Cette méthode résout aussi la question de Lagrange dans le cas où seul trois planètes sont prises en compte[19].
La preuve de Cauchy est parcellaire, il existe plus de trois planètes. Pour résoudre le cas général, il faut pouvoir trouver autant de vecteurs orthogonaux qu'il existe de planètes. Cette question, consistant à trouver une bonne famille de vecteurs orthogonaux pour une forme quadratique est finalement résolue[20] par Karl Weierstrass (1815 - 1897) en 1858. Si l'avancée mathématique est certaine, la preuve de la stabilité du système solaire n'est toujours pas faite. l'astronome Urbain Le Verrier (1811 - 1877) montre que les termes d'ordre deux ne peuvent être négligés[21].
Si les conséquences en astronomie restent douteuses, une chose est néanmoins établie. L'orthogonalité ne peut plus se limiter à la dimension trois, les services qu'elle rend sont appréciables en mathématiques comme en physique sur des espaces de dimension quelconque.[22]
Forme bilinéaire
La généralisation n'est néanmoins pas encore totale. Vers la fin du XIXe siècle Ferdinand Georg Frobenius (1849 1917) découvre une nouvelle méthode pour étudier les groupes finis. Il les représente par un groupe d'applications linéaires. Il démontre que, pour un groupe donné, chaque représentation est construite à partir d'un nombre fini de briques élémentaires[23]. Pour chacune de ces briques élémentaires, il considère une fonction, qui à chaque élément du groupe associe la trace de l'application linéaire associée. Cette application s'appelle le caractère de la représentation. Les caractères des briques élémentaires sont tous orthogonaux entre eux[24]. Cette propriété permet de déterminer simplement quelles briques élémentaires sont utilisées pour une représentation donnée. Elle est un des fondements de la théorie. Cette orthogonalité s'exprime à l'aide d'une forme bilinéaire symétrique, absolument équivalente à une forme quadratique.
Les groupes apparaissent comme un sous-ensemble de rotations dans l'espace. Si les ensembles de nombres choisis sont finis, le groupe des rotations est nécessairement fini. Cette méthode permet de construire des groupes simples, briques élémentaires pour la construction de tout groupe fini. Ces ensembles de nombres ne sont plus ordonnés, l'équivalent de la distance ne peut donc être toujours positive. Frobenius n'est de loin pas le premier à s'intéresser à cette configuration. Euler étudiait déjà en arithmétique un problème analogue à celui de Fermat : x2 - n.y2 = 1 avec une forme quadratique pas toujours positive[25]. James Joseph Sylvester (1814 1897) trouve en 1852 une loi portant son nom qui indique que toutes les bases orthogonales contiennent le même nombre de vecteurs ayant une distance positive et le même nombre ayant une distance négative[26]. Le concept d'orthogonalité s'applique alors à une forme bilinéaire, qui ne correspond plus nécessairement à une distance euclidienne. En effet, au sens propre, une distance est toujours positive.
Le formalisme moderne est plus tardif que la découverte des théorèmes fondamentaux. Les mathématiciens les découvrent souvent bien avant qu'une présentation simple et didactique soit disponible. Par exemple, le produit scalaire est une forme bilinéaire correspondant à une géométrie euclidienne. Sa définition est l'œuvre d'Hermann Weyl (1885 1955) et date de 1918[27]. Avec ce formalisme, les termes angle droit et perpendiculaire ne sont plus utilisés.
Définitions formelles
Soit (.|.) une forme bilinéaire définie sur ExF deux espaces vectoriels sur un corps K.
Définition 1 — Soit M (resp. N) une partie de E (resp. F). L'orthogonal de M (resp. N) correspond à l'ensemble des vecteurs y (resp. x) de F (resp. E) vérifiant la propriété suivante :
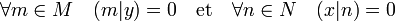 [28]
[28]L'orthogonal de M (resp. N) désigne ainsi l'ensemble des vecteurs de E (resp. F) perpendiculaires à tous les éléments de M (resp. N). Néanmoins, dans le contexte général de cette définition les termes de perpendiculaires et angle droit ne sont plus utilisés.
Définition 2 — Deux vecteurs x et y de E et F sont dit orthogonaux pour la forme bilinéaire
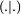 si et seulement si leur image par la forme bilinéaire est nulle :
si et seulement si leur image par la forme bilinéaire est nulle :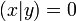
D'une manière plus générale, on dit qu'un ensemble M est orthogonal à un ensemble N si, pour tout élément m de M et tout élément n de M, l'image (m | n) est nulle.
L'orthogonal d'un ensemble M est souvent noté
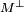 et la proposition x est orthogonal à y s'écrit
et la proposition x est orthogonal à y s'écrit 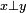 .
.Dimension finie
Espace euclidien
Un espace euclidien E est un espace vectoriel réel de dimension finie, ici noté n et muni d'un produit scalaire (.|.). Au lieu de point, on parle en général de vecteur. La distance d entre deux vecteurs x et y est donnée par la formule suivante :
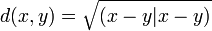
Si Φ est une partie de E, alors l'orthogonal de Φ est un sous-espace vectoriel de E et plus précisément :
proposition 1 — L'orthogonal de Φ est un sous-espace vectoriel supplémentaire de l'espace vectoriel engendré par Φ. L'orthogonal de
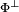 est l'espace vectoriel engendré par Φ.
est l'espace vectoriel engendré par Φ.Cette proposition est une conséquence des propriétés sur l'orthogonalité démontrées dans l'article Forme bilinéaire. Cette propriété apporte un intérêt à la notion de projecteur parallèlement à son orthogonal. Une telle application est nommée projection orthogonale. On en déduit aussi que l'orthogonal du vecteur nul est l'espace entier et l'orthogonal de l'espace entier est le vecteur nul.
Soient Φ1 et Φ2 deux parties parties de E, alors :
proposition 2 — Les relations d'orthogonalités suivantes sont vérifiées, si Vect(A) désigne l'espace vectoriel engendré par une partie A de E :
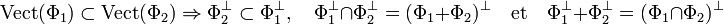
Ces relations sont démontrées dans l'article Forme bilinéaire.
L'orthogonal d'un vecteur non nul est un hyperplan et tout sous-espace vectoriel F différent de E s'exprime comme intersection d'hyperplans. Plus précisément, tout sous-espace vectoriel de codimension p, si p est un entier strictement positif, est l'intersection de p hyperplans. Comme tout hyperplan s'exprime comme l'orthogonal d'un vecteur, la deuxième propriété de la proposition 2 indique donc l'existence de p vecteurs (vi) pour i variant de 1 à p tel que :
![F= \{x \in E\; / \;\forall i \in [1,p]\;(a_i|x)=0\}](/pictures/frwiki/100/d19ce40d367e4bbfadda7b41333d4f35.png)
Enfin, le procédé d'orthogonalisation de Gram-Schmidt montre l'existence d'une base orthogonale. Si (ei), pour i variant de 1 à n, est une base orthogonale, alors tout vecteur x de E s'exprime comme une combinaison linéaire de la base à l'aide du produit scalaire et la norme de x comme une somme de carrés de produits scalaire de x avec les éléments de la base :
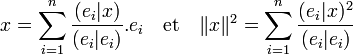
Ces propriétés se déduisent de celles démontrées dans l'article Inégalité de Bessel. Il traite aussi du cas où la famille n'est pas génératrice.
Espace hermitien
Charles Hermite (1822 1901) généralise l'approche euclidienne sur les espaces complexes qui portent maintenant son nom. Les conditions nécessaires et suffisantes d'orthogonalité précédentes ne s'appliquent plus. Si x et y sont deux vecteurs d'un espace hermitien H, on dispose de la relation suivante :
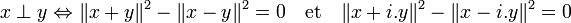
En revanche, toutes les propriétés décrites dans le paragraphe Espace euclidien restent valables.
Forme bilinéaire symétrique
Dans le cas d'une forme bilinéaire symétrique (.|.), il peut exister un sous-espace vectoriel orthogonal à l'espace entier E.
Définition — Le noyau d'une forme bilinéaire symétrique est le sous-espace des vecteurs orthogonaux à l'espace entier E. Une forme bilinéaire ayant un noyau non réduit au vecteur nul est dite dégénérée.
L'orthogonal du vecteur nul est l'espace entier et l'orthogonal de l'espace entier est le noyau. De plus, tout orthogonal d'une famille Φ contient le noyau. Soit N le noyau de la forme (.|.) et M un supplémentaire du noyau dans E. La restriction de (.|.) à M est non dégénérée. Sur cette restriction, les propositions 1 et 2 du paragraphe Espace euclidien restent valides. Ces résultats sont démontrés dans l'article Forme bilinéaire.
La réduction de Gauss montre l'existence de base orthogonal pour (.|.). Cette réduction s'applique aux formes quadratiques, cependant réduire une forme quadratique, c'est-à-dire trouver une base orthogonale pour cette forme quadratique revient à trouver une base orthogonale pour sa forme polaire. Sylvester va plus loin dans son analyse. Sa loi stipule qu'il existe un couple d'entier (q, r) tel que, pour toute base orthogonale (ei), L'expression (ei | ei) est strictement positive exactement q fois, strictement négative exactement r et que le noyau de la forme bilinéaire est de dimension n - q - r. Ici n désigne la dimension de E.
Le théorème de Weierstrass montre comment s'expriment les relations d'orthogonalités si deux formes bilinéaires symétriques dont l'une est définie positive sont en présence :
Théorème spectral en dimension finie — Soit E un espace vectoriel de dimension finie sur le corps des réels (resp. des complexes) et Φ, Ψ deux formes bilinéaires symétriques (resp. sesquilinéaire) de E tel que Φ soit définie positive. Alors il existe une base B de E orthonormale pour Φ et orthogonale pour Ψ. Dans cette base, les coefficients de la matrice associée à Ψ sont tous réels.
Ce théorème est démontré dans l'article Endomorphisme autoadjoint. Il existe un équivalent de forme bilinéaire symétrique pour les espaces complexes, ce sont les formes sesquilinéaires. Tous les résultats de ce paragraphe s'appliquent aussi à ces formes.
Cas général
Si la forme bilinéaire n'est pas symétrique, il existe encore un cas où il est possible de parler d'orthogonalité au sens précédent, celui des formes réflexives.
Définition — La forme bilinéaire est dite réflexive si et seulement si la propriété suivante est vérifiée:
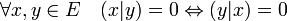
La configuration est alors la même que celle de la forme bilinéaire symétrique. Sur un supplémentaire du noyau, la forme est non dégénérée et les propositions 1 et 2 du paragraphe sur les espaces euclidiens s'appliquent. Dans le cas général l'orthogonal du vecteur nul est l'espace entier et l'orthogonal de l'espace entier est le noyau. Enfin, tous les orthogonaux contiennent le noyau.
Dans le cas général, il devient nécessaire de parler d'orthogonalité à gauche et à droite. Soit Φ une famille de vecteur, l'orthogonal à gauche de Φ est défini par l'ensemble suivant :
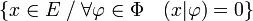
Si la forme bilinéaire est définie sur un produit ExF de deux espaces vectoriel, alors l'ambigüité n'existe pas. L'orthogonal d'une famille d'éléments de E est un sous-espace vectoriel de F et réciproquement.
La codimension des noyaux à droite et à gauche sont les mêmes. Si M1 (resp. M2) est un supplémentaire du noyau à gauche N1 (resp. à droite N2), alors tout vecteur x (resp. y) de l'espace de gauche (resp. de droite) s'exprime de manière unique comme somme d'un vecteur x1 (resp. y1) du supplémentaire du noyau et d'un vecteur du noyau. La restriction de la forme bilinéaire à M1xM2 est non dégénérée et :
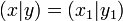
Plus de détails sur les orthogonaux dans cette configuration sont donnés dans l'article Forme bilinéaire.
Dimension infinie
Motivation
 Joseph Fourier utilise pour la première fois l'orthogonalité en dimension infinie pour résoudre l'équation de la chaleur.
Joseph Fourier utilise pour la première fois l'orthogonalité en dimension infinie pour résoudre l'équation de la chaleur.
En dimension finie, l'orthogonalité rend d'innombrables services. Il est tentant de généraliser sa définition aux espaces de dimensions quelconques et en particulier infini. Sous un formalisme un peu différent, c'est ainsi que Joseph Fourier (1768 1830) résout l'équation de la chaleur[29]. A deux fonctions f et g, on associe le produit scalaire :
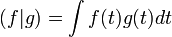
Certain problèmes issues de la physique, comme l'équation de la chaleur ou celle de la corde vibrante s'exprime comme un opérateur linéaire disposant de bonnes propriétés vis-à-vis de son adjoint. Si la configuration est particulièrement favorable, par exemple si l'opérateur est compact et autoadjoint, un résultat analogue à celui de la dimension finie apparaît. Il existe une base de vecteurs propres orthogonaux et de norme un. Le mot base prend ici une signification un peu différente de celle de la dimension finie. La famille est toujours libre, cependant ce n'est plus une combinaison linéaire qui représente un vecteur mais une série dont le carré de la norme de chaque vecteur est absolument convergente.
Puisqu'en dimension infinie les combinaisons linéaires deviennent des séries, un nouvel outil devient indispensable, la topologie, permettant de donner un sens à la limite, c'est-à-dire à l'équivalent des combinaisons linéaires. Dans le cas général, cette limite n'est garantie d'exister que si l'espace est complet. Pour cette raison, le cadre le plus simple pour étudier l'orthogonalité en dimension finie est celui d'un espace vectoriel muni d'un produit scalaire tel que la distance associée confère à l'espace la complétude. Plusieurs mathématiciens sont initiateurs de l'étude de la géométrie d'un espace vectoriel de cette nature, on peut citer Erhard Schmidt (1876 1959) ou encore Ivar Fredholm (1866 1927). David Hilbert (1862 1943) est néanmoins celui qui lui donne son nom[30]. John von Neumann (1903 1957) donne la définition moderne du concept[31].
Il existe certaines configurations où l'espace fonctionnel ne peut être équipé d'un produit scalaire. Une autre technique permet de bénéficier des propriétés d'orthogonalités, provenant de l'espace dual. En général n'est considéré que le dual topologique, c'est-à-dire celui ne contenant que les formes linéaires bornées. Une fois encore l'hypothèse de la complétude de l'espace vectoriel E est fort utile. Stefan Banach (1892 1945) propose la première formulation axiomatique moderne[32]. Son livre de 1932 sur la question[33] est encore une référence. Un espace de Banach est un espace vectoriel normé complet.
Espace de Hilbert
Espace de Banach
Dans ce paragraphe E désigne un espace de Banach et E* son dual topologique, l'unique dont il est question ici. Ainsi le produit scalaire est remplacé par une forme bilinéaire souvent noté avec le crochet de dualité <.,.> utilisé dans ce paragraphe. Cette forme, encore parfois appelée produit scalaire, est l'unique étudiée ici. En effet, toute forme bilinéaire d'un espace E dans un espace F est la composée d'un opérateur linéaire a de F dans le dual de E et du crochet de dualité. Les propriétés d'une telle forme bilinéaire sont les conséquences de celle de a et de son adjoint.
La définition de l'orthogonalité est l'application de la définition générale. Ainsi, l'orthogonal d'une partie Ψ* du dual est le sous-espace vectoriel de E composé des vecteurs orthogonaux à tous les vecteurs de Ψ*. On remarque qu'une autre définition aurait pu être utilisée, l'ensemble des éléments du bidual orthogonaux à Ψ*. Il existe une isométrie canonique entre E et le bidual, qui à x associe x** définie par :
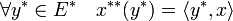
Dire que E est un espace réflexif revient à dire que l'isométrie est surjective et qu'il est possible d'identifier E avec le bidual. Dans toute la suite du paragraphe, l'orthogonal d'une partie de E* désigne toujours un sous-espace vectoriel de E, même si l'espace n'est pas réflexif.[34]
Proposition 1 — Soit F un sous espace vectoriel de E, l'orthogonal de
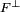 est l'adhérence de F. Soit G* un sous-espace vectoriel de E* l'orthogonal de
est l'adhérence de F. Soit G* un sous-espace vectoriel de E* l'orthogonal de 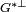 contient l'adhérence de G*. Si E est réflexif, alors l'orthogonal de
contient l'adhérence de G*. Si E est réflexif, alors l'orthogonal de 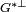 est égal à l'adhérence de G*.
est égal à l'adhérence de G*.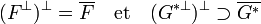
La proposition 2 pour les espaces euclidiens prend une forme légèrement différente :
Si F1 + F2 est un sous-espace fermé, alors la situation est proche de la configuration euclidienne. Le résultat suivant est plus profond, en conséquence, il est plus subtile à démontrer :
proposition 3 — Les quatre propositions suivantes sont équivalentes :
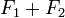 est un sous-espace fermé de E.
est un sous-espace fermé de E.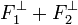 est un sous-espace fermé de E*.
est un sous-espace fermé de E*.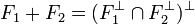 .
.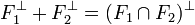 .
.
Démonstrations-
- L'orthogonal de
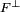 est l'adhérence de F :
est l'adhérence de F :
- L'orthogonal de
Remarquons dans un premier temps qu'un orthogonal est un sous espace fermé. Soit (xn) une suite de l'orthogonal d'une famille Φ* convergeant vers x. Soit x* un élément de Φ* :
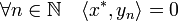
Un passage à la limite montre que y est aussi élément de l'orthogonal de Φ*. L'adhérence de F est donc contenu dans l'orthogonal de
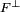 .
.Réciproquement raisonnons par l'absurde. Soit x un élément de l'orthogonal de
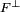 qui ne soit pas dans l'adhérence de F. Définissons S comme la somme directe de l'espace vectoriel engendré par x et F. Considérons la forme linéaire y1* qui à tout vecteur λ.x + f de S associe λ. C'est une forme linéaire continue. La forme géométrique du théorème de Hahn-Banach montre l'existence d'une forme linéaire continue y* qui prolonge y1* sur E. Cette forme linéaire est nulle sur F et a pour image de x le scalaire un. la forme y* est élément de l'orthogonal de F, mais n'est pas orthogonal à x, en conséquence x n'est pas dans l'orthogonal de
qui ne soit pas dans l'adhérence de F. Définissons S comme la somme directe de l'espace vectoriel engendré par x et F. Considérons la forme linéaire y1* qui à tout vecteur λ.x + f de S associe λ. C'est une forme linéaire continue. La forme géométrique du théorème de Hahn-Banach montre l'existence d'une forme linéaire continue y* qui prolonge y1* sur E. Cette forme linéaire est nulle sur F et a pour image de x le scalaire un. la forme y* est élément de l'orthogonal de F, mais n'est pas orthogonal à x, en conséquence x n'est pas dans l'orthogonal de 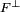 . Cette contradiction montre que tout élément de l'orthogonal de
. Cette contradiction montre que tout élément de l'orthogonal de 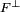 est élément de l'adhérence de F et conclut la démonstration.
est élément de l'adhérence de F et conclut la démonstration.-
- L'orthogonal de
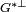 contient l'adhérence de G*. Si E est réflexif, alors l'orthogonal de
contient l'adhérence de G*. Si E est réflexif, alors l'orthogonal de 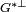 est égal à l'adhérence de G* :
est égal à l'adhérence de G* :
- L'orthogonal de
Montrons que
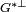 contient l'adhérence de G*. Soit (yn*) une suite de G* convergeant vers une limite y*. Soit x un élément de
contient l'adhérence de G*. Soit (yn*) une suite de G* convergeant vers une limite y*. Soit x un élément de 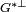 , alors :
, alors :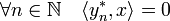
Un passage à la limite montre que y est orthogonal à x et donc orthogonal à
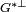 . Ceci montre que l'orthogonal de
. Ceci montre que l'orthogonal de 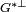 contient l'adhérence de G*.
contient l'adhérence de G*.Réciproquement, supposons E réflexif. On raisonne par l'absurde comme précédemment. Soit y* un élément de l'orthogonal de
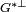 qui ne soit pas dans l'adhérence de G*. Définissons S* comme la somme directe de l'espace vectoriel engendré par y* et F*. Considérons la forme linéaire x1** qui à tout vecteur λ.y* + f* de S* associe λ. C'est une forme linéaire continue. La forme géométrique du théorème de Hahn-Banach montre l'existence d'une forme linéaire continue x** qui prolonge x1** sur E**. Comme E est réflexif, il existe un vecteur x de E tel que la forme linéaire sur E* associée à x soit égal à x**. La fin du raisonnement est analogue au précédent.
qui ne soit pas dans l'adhérence de G*. Définissons S* comme la somme directe de l'espace vectoriel engendré par y* et F*. Considérons la forme linéaire x1** qui à tout vecteur λ.y* + f* de S* associe λ. C'est une forme linéaire continue. La forme géométrique du théorème de Hahn-Banach montre l'existence d'une forme linéaire continue x** qui prolonge x1** sur E**. Comme E est réflexif, il existe un vecteur x de E tel que la forme linéaire sur E* associée à x soit égal à x**. La fin du raisonnement est analogue au précédent.-
- Proposition 2 :
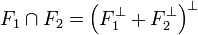
Soit x un élément de l'intersection, il est orthogonal à tout élément de
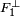 et de
et de 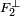 dont à tout élément de la somme. En conséquence l'intersection est incluse dans l'orthogonal de la somme.
dont à tout élément de la somme. En conséquence l'intersection est incluse dans l'orthogonal de la somme.Réciproquement, la somme des orthogonaux de F1 et F2 contient tout élément de l'orthogonal de l'intersection de F1 et F2. Comme l'intersection de deux fermés est un fermé, la proposition 1 permet de conclure que :
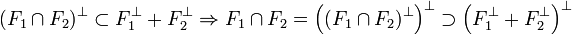
Ce qui termine la démonstration.
C'est une conséquence de la proposition précédente et de la proposition 1.
Considérons un élément de l'intersection, il est par définition orthogonal à tout élément de F1 et de F2. L'intersection est donc incluse dans l'orthogonal de la somme. Réciproquement soit un élément de l'orthogonal de la somme. Il est, par définition orthogonal aux élément de F1 et de F2, ce qui termine la démonstration.
C'est une conséquence de la proposition précédente et de la proposition 1.
-
- Les quatre propositions suivantes sont équivalentes :
-
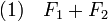 est un sous-espace fermé de E.
est un sous-espace fermé de E.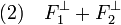 est un sous-espace fermé de E*.
est un sous-espace fermé de E*.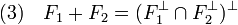 .
.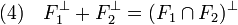 .
.
- (1) est équivalent à (3) :
Cette proposition est une conséquence directe de la proposition précédente.
- (4) implique (2) :
Si (4) est vraie, alors la somme est égal à un orthogonal, comme tout orthogonal est fermé, la somme est fermée.
- (1) implique (4)
Réciproquement, si (2) est vraie, une proposition précédente montre que la somme des orthogonaux est incluse dans l'orthogonal de l'intersection. Soit y* un élément de l'orthogonal de l'intersection. Soit G la somme de F1 et de F2. Tout élément x de G est somme d'un élément x1 de F1 et d'un élément x2 de F2. Soit z2* l'application qui à x associe < y* , x1>. Comme y* est la forme linéaire nulle sur l'intersection de F1 et F2, l'image de x par z2* est bien définie. La forme z2* est clairement liénaire. De plus, un corollaire du théorème de Banach-Schauder, dit de l'application ouverte montre qu'il existe une constante C strictement positive telle que (la démonstration du corollaire est donnée dans l'article associée):
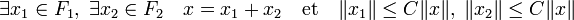
Cette propriété montre la continuité de z2*. Le théorème de Hahn-Banach sous sa forme géométrique montre qu'il est possible de prolonger z2* en une forme linéaire continue y2* sur E. Définissons y1* comme la différence y* - y2*. La forme y1* est nulle sur F1 et y2* est nulle sur F2. Ce qui montre que y* est bien élément de la somme des orthogonaux.
-
- (2) implique (1) :
Applications
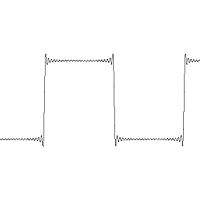
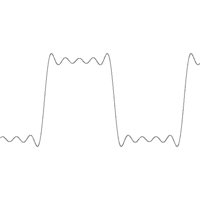 Décomposition d'une fonction créneau sur des sinusoïdes. Seuls les dix premières sinusoïdes sont utilisées, proposant ainsi une approximation.
Décomposition d'une fonction créneau sur des sinusoïdes. Seuls les dix premières sinusoïdes sont utilisées, proposant ainsi une approximation.
La première application historique de l'orthogonalité en dimension infinie a pour objectif de résoudre une équation aux dérivées partielles. La nature offre de nombreux exemples où l'équation se traduit par un opérateur linéaire. Tel est le cas, par exemple pour l'équation d'onde qui régit les mouvements d'une corde vibrante. Cette équation se résout simplement si la position initiale de la corde est une sinusoïde de période la longueur de la corde divisée par un entier. Ces cas particuliers possèdent deux propriétés importantes. L'espace vectoriel approxime aussi précisément que souhaité toutes les positions initiales que peut prendre la corde (elle est supposée ne pas rompre, ce qui signifie que la position initiale est représentée par une fonction continue). De plus cette famille sinsoïdale est orthogonale, l'inégalité de Bessel permet de déterminer une combinaison linéaire qui approxime aussi précisément que souhaité la position initiale ou propose une série convergente vers cette position. Les figures de droite et de gauche illustrent deux approximations de la fonction créneau. La linéarité de l'opérateur permet d'évaluer la trajectoire de la corde par combinaison linéaire ou série. Cette technique, consistant à décomposer une fonction sur une famille orthogonale est à l'origine d'une vaste branche des mathématiques, appelée analyse harmonique.
Pour cette raison, de nombreuses familles orthogonales ont été construites. Les polynômes orthogonaux, comme ceux de Legendre, d'Hermite ou de Laguerre sont de cette nature. Ils correspondent à trois produits scalaires différents.
Le théorème de Weierstrass possède son équivalent sur un Hilbert. L'opérateur doit non seulement être autoadjoint mais aussi compact. Cette configuration correspond à une équations intégrales étudiée par Hilbert et Schmidt. Comme en dimension finie, il existe une base de vecteurs propres orthogonaux. Cette équation intégrale possède une signification profonde en physique, elle représente par exemple les équations de Maxwell.
La bonne propriété topologique de compacité n'est pas toujours présente. L'équation de Schrödinger est un exemple d'opérateur autoadjoint non compact, il n'est d'ailleurs pas continu. S'il existe toujours des vecteurs propres et s'ils sont toujours orthogonaux, ils ne forment plus une base de l'espace des solutions. Une fois encore, il est nécessaire d'élargir les définitions pour que les concepts restent opérationnels. Une valeur λ est dite spectrale pour l'opérateur a si a -λ.Id n'est pas inversible. Il se peut que a -λ.Id soit injectif et non surjectif. Dans ce cas, il n'existe pas de vecteur propre. Une autre théorie devient nécessaire, appelée théorie spectrale.
La physique ne se contente pas des espaces de Hilbert. Un phénomène peut être suffisamment discontinu pour sortir du Hilbert, il est parfois modélisé par un pic de Dirac, une espèce de fonction valant zéro partout sauf en un point ou elle vaudrait l'infini. Elle représente par exemple une probabilité de présence nulle partout sauf en un point où la position est certaine. Pour enrichir l'espace fonctionnel, il devient nécessaire d'utiliser des Banach et la théorie des distributions. Le produit scalaire devient le crochet de dualité.
Si la physique est à l'origine de la généralisation de l'orthogonalité aux dimensions infinies, elle n'est de loin pas la seule cliente. La théorie des représentations s'étend aux groupes continus. Les caractères deviennent des fonctions du groupe à valeur dans les nombres complexes. A l'aide d'une mesure, comparable à l'intégrale sur les réels, un produit scalaire est défini. Les relations d'orthogonalités du cas fini se généralisent. Une fois encore, la décomposition en briques élémentaires est donnée par des relations d'orthogonalités entre les caractères. Cette approche consistant à décomposer une fonction sur une famille orthogonale est de même nature que celle utilisée pour étudier les mouvements d'une corde vibrante. Si le groupe choisi est celui des nombres complexes de module un, les résultats obtenus sont identiques. on retrouve par un autre chemin la théorie de l'analyse harmonique. Il devient possible de la généraliser à bien d'autres groupes.
Informatique
Le jeu d'instructions d'un ordinateur est dit orthogonal lorsque (presque) toutes les instructions peuvent s'appliquer à tous les types de données. Un jeu d'instruction orthogonal simplifie la tâche du compilateur puisqu'il y a moins de cas particuliers à traiter : les opérations peuvent être appliquées telles quelles à n'importe quel type de donnée. Un exemple typique est le VAX ou le PDP-10.
Notes et références
Notes
- ↑ Deledicq André Traduction d'Euclide Peyrard 1804 les Eléments d'Euclide pour le collège et le Lycée Les éditions du Kangourou 1999
- ↑ David Hilbert Grundlagen der Geometrie 1ière éd. 1899, B.G. Teubner, Leipzig version anglaise
- ↑ Le professeur Alexander Thom montre que des Mégalithes d'Europe du nord suivent un alignement associé à des triplets pythagoriciens : A. Thom Megalithic Geometry in Standing Stones New Scientist 12 mars 1964 Megalithic triangles
- ↑ Cette attribution ne date pas d'hier. On la trouve par exemple dans : J.N. Haton de la Goupillière Mémoire sur une théorie nouvelle de la géométrie des masses Journal de l'Ecole Impériale de Polytechnique N° 36 T 21 p 77
- ↑ Cette attribution est l'œuvre de Proclos, pour Heath : T. L. Heath A history of Greek mathematics Vol I Dover Publications; New Ed edition (ISBN 0486240738)
- ↑ E. Robson D. Fowler Square root approximations in Old Babylonian mathematics : YBC 7289 in context, Historia Mathematica, 25, pp. 366-378 1998
- ↑ a et b Apollonius de Perge Les Coniques d’Apollonius de Perge trad. P. Ver Eecke, 1922, rééd. Blanchard, Paris, 1963
- ↑ Michel Chasles en parle longuement dans son livre : Aperçu historique sur l'origine et le développement des méthodes en géométrie Hayez Bruxelles 1837 p 19 Lire
- ↑ M. Housel Les coniques d'Apollonius Journal de Mathématiques Pures et Appliquées Paris. Vol 3 1858 p 154 Lire
- ↑ René Descartes La Géométrie, Hollande p 1 1637 lire
- ↑ René Descartes La Dioptrique Hollande 1637 lire
- ↑ Isaac Newton 1687 Philosophiae Naturalis Principia Mathematicalire
- ↑ Pierre de Fermat Correspondance Marin de Mersenne 25 Décembre 1640
- ↑ Le résultat est annoncé dans une lettre d'Euler à Christian Goldbach le 12 avril 1749
- ↑ Joseph-Louis Lagrange Recherche d'arithmétique seconde partie Nouveaux mémoires de l'Académie royale des sciences et belles lettres de Berlin 1775 Oeuvres, vol III p 695, 795. Le théorème est démontré sous le nom de Lemme VII p 782, 783
- ↑ On peut citer Carl Friedrich Gauss, Johann Peter Gustav Lejeune Dirichlet, Karl Weierstrass, Leopold Kronecker et David Hilbert. Cette histoire est analysée dans l'article suivant : F. Lemmermeyer The Shaping of Arithmetic after C. F. Gauss’s Disquisitiones Arithmeticae Springer Berlin Heidelberg 2007 (ISBN 978-3-540-20441-1) p 529 561 lire
- ↑ Joseph-Louis Lagrange Théorie des variations séculaires des éléments des planètes Nouv. mém. de l’acad. des sciences de Berlin Vol 1 p 125 1783
- ↑ Augustin Louis Cauchy Sur les centres, les plans principaux et les axes principaux des surfaces du second degré Exer. de math.3 = Œuvres (2)8, pp 8 35 1828
- ↑ Augustin Louis Cauchy Sur l’équation à l’aide de laquelle on détermine les inégalités séculaires du mouvement des planètes Exer. de math. 4 = Œuvres (2)9, pp 174 195 1829
- ↑ Karl Weierstrass Uber ein die homogenen Functionen zweiten Grades betreffendes Theorem M’ber. Akad. der Wiss. Berlin 1858 traduction Frédéric Brechenmacher
- ↑ Jacques Laskar La stabilité du système solaire Seuil pp 184-187 1992 (ISBN 2-02-015182-0) Lire
- ↑ L'analyse des prolégomènes du théorème de Weierstrass provient de l'article : F. Brechenmacher L'identité algébrique d'une pratique portée par la discussion sur l'équation à l'aide de laquelle on détermine les inégalités séculaires des planètes Chapitre extrait d'une thèse de doctorat sous la direction de J. Dhombre lire
- ↑ Ferdinand Georg Frobenius Uber die Darstellung der Endlichen Gruppen durch linear Substitutionen, Sitzungsber. Preuss Akad. Wiss Berlin 1897
- ↑ Ferdinand Georg Frobenius Zur Theorie der Scharen bilinearer Formen Zürich 1896
- ↑ Cette équation porte le nom de Pell-Fermat. Son histoire est étudiée dans la référence suivante :André Weil Number Theory: An approach through history from Hammurapi to Legendre Birkhäuser Boston 1987 (ISBN 0817631410)
- ↑ James Joseph Sylvester A démonstration of the theorem that every homogeneous quadratic polynomial is reducible by real orthogonal substitutions to the form of sum of positive and negative square Philosophical magazine IV 1852 p 138-142 lire
- ↑ Hermann Weyl Temps, espace, matière A. Blanchard 1979 (ISBN 2853670333)
- ↑ Cette définition correspond par exemple à celle de Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions] p 22
- ↑ Joseph Fourier Théorie analytique de la chaleur Firmin Didot Père et Fils Paris 1822. Réédition Jacques Gabay 1988 (ISBN 2876470462)
- ↑ Hermann Weyl David Hilbert and His Mathematical Work Bulletin of the American Mathematical Society 60 1944 p 612-654
- ↑ John von Neumann Zur Algebra der Funktionaloperatonen Mathematische Annalen N° 102 1930, pp. 370-427
- ↑ Stefan Banach Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales Fundamenta Matematicae 1922 Lire
- ↑ Stefan Banach Theorie Des Operations Lineaires Chelsea Pub Co 2nd Ed 1999 (ISBN 0828401101) Lire
- ↑ Les propositions ainsi que les démonstrations suivantes sont largement inspirées du Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions] p 23-26
Liens externes
- (fr) Orthogonalité dans l'espace par J. Onillon 2003. Ce site couvre le paragraphe intitulé géométrie d'Euclide.
- (fr) Géométrie dans l'espace en seconde par D. Nivaud 2001
- (fr) Orthogonalité Les Mathématiques.net par C.Antonini, J.F. Quint, P. Borgnat, J. Bérard, E. Lebeau, E. Souche, A. Chateau, O. Teytaud 2001.
- (fr) Orthogonalité, orthogonalisation de Gram-Schmidt par L'Université de Nantes A. Morame 2006
- (fr) Compléments d'algèbre bilinéaire Mortajine A. Latif de l'Université Henri Poincaré-Nancy 1 2007
Références
Ouvrages mathématiques
- F. Casiro, A. Deledick Pythagore et Thalès Les éditions du Kangourou 1998 (ISBN 2-87694-040-X)
Un ouvrage didactique sur les bases de la géométrie avec quelques éléments relatifs à l'histoire. Il couvre l'orthogonalité pour la géométrie d'Euclide
- Y. Sortais La Géométrie du triangle. Exercices résolus Hermann 1997, (ISBN 270561429X)
Ce livre s'adresse essentiellement aux élèves de la seconde à la terminale, ainsi qu'à leur professeur. Il propose des exercices sur le théorème de Thalès, la projection orthogonale, l'homothétie, la symétrie et la rotation, le calcul barycentrique, le produit scalaire, ou encore la notion d'angle.
- Y. Ladegaillerie Géométrie pour le CAPES de mathématiques Ellipses Marketing 2002 (ISBN 2729811486)
Ce livre traite de géométrie élémentaire au programme du CAPES. Il contient plus de 600 figures géométriques et couvre la géométrie affine euclidienne ainsi que l'algèbre linéaire élémentaire.
- Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808)[détail des éditions]
Ce livre couvre de manière extensive l'orthogonalité en dimension finie. Il est d'un niveau soutenu pour la dimension finie.
- Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
Haïm Brezis propose une introduction à l'analyse fonctionnelle. Le livre présente à la fois l'aspect théorique et les applications.
- B. Beauzamy Introduction to Banach spaces and their geometry Elsevier Science 1985 (ISBN 0444878785)
Un livre spécialisé sur les espaces de Banach. S'il est relativement exhaustif, son niveau est soutenu.
Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz
- Portail des mathématiques
Catégories : Algèbre bilinéaire | Espace vectoriel normé
Wikimedia Foundation. 2010.