Invariants De Similitude
- Invariants De Similitude
-
Invariants de similitude
En algèbre linéaire, un système complet d'invariants pour la relation de similitude entre les matrices carrées de même taille à coefficients dans un corps est connu : ces invariants sont classiquement appelés invariants de similitude. Ils consistent en une suite finie de polynômes totalement ordonnée pour la relation de divisibilité, dont les deux extrêmes sont le polynôme caractéristique et le polynôme minimal.
On peut montrer que, si A est une matrice carrée de taille n à coefficients dans le corps  , alors il existe une matrice diagonale par blocs B de même taille qui soit semblable à A, et dont les blocs diagonaux soient les matrices compagnons de certains polynômes de
, alors il existe une matrice diagonale par blocs B de même taille qui soit semblable à A, et dont les blocs diagonaux soient les matrices compagnons de certains polynômes de ![\mathbb{K}[X]](/pictures/frwiki/97/a54a58150f8fbfa21e4e47bea7551681.png) , totalement ordonnés par la divisibilité, et que la suite de ces polynômes, à multiplication par des inverses près, caractérise entièrement la classe de similitude de A : ce sont les invariants de similitude. L'existence d'une telle matrice B repose sur la structure de
, totalement ordonnés par la divisibilité, et que la suite de ces polynômes, à multiplication par des inverses près, caractérise entièrement la classe de similitude de A : ce sont les invariants de similitude. L'existence d'une telle matrice B repose sur la structure de ![\mathbb{K}[X]](/pictures/frwiki/97/a54a58150f8fbfa21e4e47bea7551681.png) -module de type fini, induite sur l'espace vectoriel
-module de type fini, induite sur l'espace vectoriel 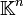 par la multiplication à gauche par les polynômes en A, et l'application à cette structure du théorème des facteurs invariants : les invariants de similitude se trouvent être les facteurs invariants de cette structure de
par la multiplication à gauche par les polynômes en A, et l'application à cette structure du théorème des facteurs invariants : les invariants de similitude se trouvent être les facteurs invariants de cette structure de ![\mathbb{K}[X]](/pictures/frwiki/97/a54a58150f8fbfa21e4e47bea7551681.png) -module.
-module.
Le calcul de ces invariants de similitude est effectif par des algorithmes du type pivot de Gauss.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Algèbre linéaire
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Invariants De Similitude de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Invariants de similitude — En algèbre linéaire, un invariant de similitude est une quantité qu on peut associer à toute matrice carrée (à coefficients dans un corps commutatif fixé K), telle que pour deux matrices semblables cette quantité soit toujours la même. Exemples d … Wikipédia en Français
Invariant de similitude — Invariants de similitude En algèbre linéaire, un système complet d invariants pour la relation de similitude entre les matrices carrées de même taille à coefficients dans un corps est connu : ces invariants sont classiquement appelés… … Wikipédia en Français
Theoreme des facteurs invariants — Théorème des facteurs invariants En mathématiques, le théorème des facteurs invariants porte sur les modules de type fini sur les anneaux principaux. Les facteurs invariants sont des obstructions à l inversibilité des matrices qui n apparaissent… … Wikipédia en Français
Théorème des facteurs invariants — En mathématiques, le théorème des facteurs invariants porte sur les modules de type fini sur les anneaux principaux. Les facteurs invariants sont des obstructions à l inversibilité des matrices qui n apparaissent pas dans la théorie des espaces… … Wikipédia en Français
Loi de similitude — Grandeur sans dimension En physique, une grandeur sans dimension est une quantité permettant de décrire une caractéristique physique sans dimension ni unité explicite d expression. Elle est constituée du produit ou rapport de grandeurs à… … Wikipédia en Français
Facteur invariant — Théorème des facteurs invariants En mathématiques, le théorème des facteurs invariants porte sur les modules de type fini sur les anneaux principaux. Les facteurs invariants sont des obstructions à l inversibilité des matrices qui n apparaissent… … Wikipédia en Français
Matrices semblables — Article détaillé : réduction d endomorphisme. En mathématiques, deux matrices carrées A et B sont dites semblables s il existe une matrice inversible P telle que : A = PBP − 1. Il s agit d une relation d équivalence. Deux matrices sont… … Wikipédia en Français
Matrice (mathématiques) — Pour les articles homonymes, voir Matrice. En mathématiques, les matrices sont des tableaux de nombres qui servent à interpréter en termes calculatoires et donc opérationnels les résultats … Wikipédia en Français
Matrice Semblable — Article détaillé : réduction d endomorphisme. En mathématiques, deux matrices carrées A et B sont dites semblables s il existe une matrice inversible P telle que : A = PBP − 1. Il s agit d une relation d équivalence. Deux matrices sont… … Wikipédia en Français
Matrice semblable — Article détaillé : réduction d endomorphisme. En mathématiques, deux matrices carrées A et B sont dites semblables s il existe une matrice inversible P telle que : A = PBP − 1. Il s agit d une relation d équivalence. Deux matrices sont… … Wikipédia en Français
 , alors il existe une matrice diagonale par blocs B de même taille qui soit semblable à A, et dont les blocs diagonaux soient les matrices compagnons de certains polynômes de
, alors il existe une matrice diagonale par blocs B de même taille qui soit semblable à A, et dont les blocs diagonaux soient les matrices compagnons de certains polynômes de ![\mathbb{K}[X]](/pictures/frwiki/97/a54a58150f8fbfa21e4e47bea7551681.png) , totalement ordonnés par la divisibilité, et que la suite de ces polynômes, à multiplication par des inverses près, caractérise entièrement la classe de similitude de A : ce sont les invariants de similitude. L'existence d'une telle matrice B repose sur la structure de
, totalement ordonnés par la divisibilité, et que la suite de ces polynômes, à multiplication par des inverses près, caractérise entièrement la classe de similitude de A : ce sont les invariants de similitude. L'existence d'une telle matrice B repose sur la structure de ![\mathbb{K}[X]](/pictures/frwiki/97/a54a58150f8fbfa21e4e47bea7551681.png) -module de type fini, induite sur l'espace vectoriel
-module de type fini, induite sur l'espace vectoriel 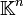 par la multiplication à gauche par les polynômes en A, et l'application à cette structure du théorème des facteurs invariants : les invariants de similitude se trouvent être les facteurs invariants de cette structure de
par la multiplication à gauche par les polynômes en A, et l'application à cette structure du théorème des facteurs invariants : les invariants de similitude se trouvent être les facteurs invariants de cette structure de ![\mathbb{K}[X]](/pictures/frwiki/97/a54a58150f8fbfa21e4e47bea7551681.png) -module.
-module.
