- Orientation (mathematiques)
-
Orientation (mathématiques)
En mathématiques, une orientation est une convention à fixer pour l'objet étudié, dont la formulation dépend de la nature de cet objet. Elle se révèle nécessaire par exemple, pour régler des problèmes de signes. Si l'espace
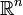 possède une orientation canonique, l'orientation d'espaces vectoriels ou de figures géométriques en général relève d'une convention arbitraire. Tous les objets concernés n'admettent pas forcément une orientation : si tel est le cas, ils sont dits orientables.
possède une orientation canonique, l'orientation d'espaces vectoriels ou de figures géométriques en général relève d'une convention arbitraire. Tous les objets concernés n'admettent pas forcément une orientation : si tel est le cas, ils sont dits orientables.Sommaire
Approche intuitive
Pour se repérer dans son espace de vie, être capable de communiquer sa position ou sa trajectoire, il est nécessaire d'appréhender et de définir des orientations. Aussi l'Homme a-t-il inventé les vocables de gauche et de droite, d'avant et d'arrière, de haut et de bas, d'est et d'ouest, de nord et de sud. Cependant, ces vocables ne sont pas de même essence. La définition du haut et du bas est liée à celle du champ gravitationnel, celle d'avant et d'arrière est liée à une ligne de vision, celle d'est et d'ouest est liée au lever et au coucher du Soleil : elles relèvent d'expériences directes. La notion de gauche et de droite, ou de nord et de sud est d'une autre nature : elles ne relèvent pas d'une expérience, mais d'une convention arbitraire. La difficulté qu'éprouvent certaines personnes à distinguer la droite de la gauche montre que la notion d'orientation n'est pas si simple que cela à percevoir. Elle exige en effet d'introduire une rupture dans une configuration perçue a priori comme ayant une certaine symétrie, et de s'entendre sur des conventions communes.
En mathématique, la mise en place de l'orientation s'est d'abord effectuée sur des objets simples – la droite, le plan, l'espace – en s'appuyant souvent sur l'intuition. Le mathématicien s'est ensuite attaché à définir l'orientation de manière plus rigoureuse et sur des objets plus complexes comme les lignes courbes, les espaces de dimension n et les surfaces.
La droite
On oriente une droite en choisissant sur celle-ci un sens de parcours, c'est à dire un vecteur unitaire[1]
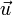 . Le parcours de A vers B est dit positif si le vecteur
. Le parcours de A vers B est dit positif si le vecteur 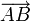 est un multiple positif du vecteur
est un multiple positif du vecteur 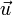 , c'est-à-dire si les deux vecteurs ont le même sens.
, c'est-à-dire si les deux vecteurs ont le même sens.On ne peut choisir que deux vecteurs unitaires différents sur une même droite, il y a donc deux orientations possibles de la droite. Aucune orientation n'a de raison objective d'être privilégiée. Par tradition seulement, une droite parallèle à la ligne d'écriture sera orientée de la gauche vers la droite comme la lecture du français.
Le plan
On oriente le plan en choisissant deux vecteurs unitaires orthogonaux (base orthonormale)[2]. On est alors capable d'orienter le cercle unité puis les angles. Si le plan est orienté par la base orthonormale
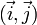 et si, dans le repère
et si, dans le repère 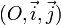 , les points A et B ont pour coordonnées respectives (1 ; 0) et (0 ; 1), le parcours le plus court sur le cercle du point A au point B sera dit parcours positif et l'angle correspondant sera dit angle droit positif.
, les points A et B ont pour coordonnées respectives (1 ; 0) et (0 ; 1), le parcours le plus court sur le cercle du point A au point B sera dit parcours positif et l'angle correspondant sera dit angle droit positif.Deux bases orthonormales superposables par rotation définissent la même orientation du cercle unité. On distingue alors deux orientations possibles du plan. Une base orthonormale étant donnée, changer un vecteur en son opposé ou permuter les deux vecteurs change l'orientation du plan.
La culture et l'invention des horloges a permis de nommer ces deux orientations. Une orientation dans laquelle les aiguilles d'une horloge tournent dans le sens positif est appelée orientation horaire ou sens des aiguilles d'une montre. En mathématique, on privilégie plutôt l'autre orientation appelée orientation anti-horaire ou sens trigonométrique.
L'espace
Orienter l'espace, c'est choisir trois vecteurs unitaires deux à deux orthogonaux (base orthonormale).
On dit que deux bases définissent la même orientation si, par rotation autour d'un axe, on peut les superposer. De nouveau, deux types d'orientation sont possibles. Une base
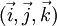 étant donnée, changer un vecteur en son opposé ou permuter deux vecteurs modifie l'orientation du plan. Opérer une permutation circulaire des trois vecteurs ne change pas l'orientation :
étant donnée, changer un vecteur en son opposé ou permuter deux vecteurs modifie l'orientation du plan. Opérer une permutation circulaire des trois vecteurs ne change pas l'orientation : 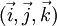 et
et 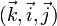 définissent la même orientation.
définissent la même orientation.La culture, ici aussi, a privilégié un sens appelé direct : celui correspondant au vissage d'une vis ou d'un tire-bouchon. La base
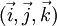 est dite directe si, en tournant de
est dite directe si, en tournant de 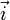 vers
vers 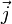 , la vis ou le tire-bouchon s'enfonce dans la direction
, la vis ou le tire-bouchon s'enfonce dans la direction 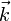 . C'est ainsi que l'orientation (haut, droite, devant) est directe et permet accessoirement de distinguer la droite et la gauche. C'est la même orientation directe que l'on trouve avec la règle des trois doigts de la main droite : le triplet (pouce, index, majeur) définit une orientation directe. On voit donc que le choix d'une orientation est liée à la notion de droite et de gauche.
. C'est ainsi que l'orientation (haut, droite, devant) est directe et permet accessoirement de distinguer la droite et la gauche. C'est la même orientation directe que l'on trouve avec la règle des trois doigts de la main droite : le triplet (pouce, index, majeur) définit une orientation directe. On voit donc que le choix d'une orientation est liée à la notion de droite et de gauche.Il est cependant évident que ces définitions s'appuyant sur un contexte culturel ne peuvent pas être satisfaisantes pour un mathématicien et qu'il s'est révélé nécessaire de donner des définitions plus générales et non contingentes. Cette définition s'établira à l'aide de la notion de déterminants.
Orientation d'une courbe
L'orientation d'une courbe (en toute rigueur, différentiable) est imposée par le choix d'une paramétrisation. Une courbe a exactement deux orientations. Intuitivement, l'orientation d'une courbe est un sens de parcours : si on se représente une courbe par une route à double sens, il y a deux façons différentes de la parcourir suivant le sens dans lequel on roule. Formellement, deux paramétrisations définissent la même orientation lorsque les vecteurs dérivés sont positivement proportionnels ; on définit ainsi une relation d'équivalence sur l'ensemble des paramétrisations d'une courbe, et on dispose de deux classes d'équivalence distinctes, appelées orientations. Si c(t) est un paramétrage de la courbe (t est un paramètre réel), le sens direct est le sens dans lequel t augmente. L'application t
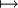 c(-t) est un autre paramétrage qui définit la seconde orientation.
c(-t) est un autre paramétrage qui définit la seconde orientation.Pour une courbe définie dans un espace vectoriel réel euclidien E, l'abscisse curviligne est une version orientée de la longueur. A une constante additive près, sa définition dépend d'un choix arbitraire de signe qui correspond exactement au choix d'une orientation de la courbe. L'abscisse curviligne augmente quand on parcourt la courbe dans le sens direct, et diminue donc dans l'autre sens. On peut choisir librement son origine, c'est-à-dire le point où elle prend la valeur 0. L'abscisse curviligne est alors positive ou négative selon qu'on est en-deçà ou au-delà de l'origine.
Un premier exemple parlant est celui du cercle unité. Il est vu comme une courbe de R2 définie par :
![c(t)=\left[\cos(t), \sin(t)\right]](/pictures/frwiki/50/241d6a003d931a1161343148ebbc1dd0.png) .
.
Ce paramétrage naturel définit une orientation du cercle unité, appeléé orientation trigonométrique ou sens anti-horaire.
Un exemple plus élémentaire est une droite affine D d'un espace vectoriel réel E (éventuellement de dimension infinie). Les paramétrages classiques sont donnés par le choix d'un point M de D et d'un vecteur directeur v de D ; le paramétrage correspondant est t
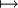 M+t·v. De tels paramétrages définissent la même orientation de D lorsque les vecteurs directeurs correspondants sont positivement colinéaires. La droite réelle R est naturellement orientée par les réels positifs.
M+t·v. De tels paramétrages définissent la même orientation de D lorsque les vecteurs directeurs correspondants sont positivement colinéaires. La droite réelle R est naturellement orientée par les réels positifs.Orientation d'un espace affine
L'orientation d'une droite affine dépend du choix d'un vecteur directeur, ou plutot du choix d'un tel vecteur à positive colinéarité près. Le choix d'une orientation pour un espace affine de dimension finie doit donc dépendre du choix d'un repère ; mais l'origine doit jouer un role secondaire dans la définition. L'orientation est donc imposée par le choix d'une base de l'espace directeur.
Deux bases d'un espace vectoriel réel E définissent la même orientation lorsque le déterminant de la matrice de passage est (strictement) positif. Cette matrice est évidemment inversible : son déterminant est donc non nul. Est ainsi définie une relation d'équivalence sur l'ensemble des bases de E, relation admettant exactement deux classes d'équivalence, les orientations de E. Une fois fixée une orientation, une base de E est dite base directe ou base indirecte selon que cette base définit l'orientation choisie ou l'autre. Une orientation d'un espace affine est une orientation de l'espace directeur. Le vocabulaire correspondant est repère direct ou repère indirect.
L'espace Rn admet une base canonique, et donc une orientation canonique.
Cette définition généralise fort heureusement la situation en dimension 1.
Orientation d'un plan
Pour un plan vectoriel P, le choix d'une orientation est imposé par le choix de deux vecteurs non colinéaires, formant donc une base
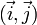 . Intuitivement, l'orientation d'un plan consiste à définir la manière de tourner autour d'un point. On tourne autour de 0 en parcourant une courbe enfermant 0, en allant de
. Intuitivement, l'orientation d'un plan consiste à définir la manière de tourner autour d'un point. On tourne autour de 0 en parcourant une courbe enfermant 0, en allant de 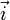 en direction de
en direction de 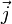 et en retournant à
et en retournant à 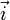 sans faire demi-tour. Il n'est donc pas étonnant à ce que la question de l'orientation soit lié au problème des angles orientés en géométrie euclidienne.
sans faire demi-tour. Il n'est donc pas étonnant à ce que la question de l'orientation soit lié au problème des angles orientés en géométrie euclidienne.L'orientation d'un plan vectoriel euclidien E se résume essentiellement au choix d'une orientation de son cercle unité. Cette orientation revient à fixer un signe au niveau des mesures d'angle.
Par le théorème de Jordan, une courbe de Jordan, c'est-à-dire une courbe périodique et simple (injective sur une période), d'un plan orienté P borde un domaine compact du plan P (voir figure). Il existe donc une notion naturelle d'intérieur et d'extérieur. On impose à un paramétrage c que pour tout vecteur sortant n(t) en c(t), (c '(t), n(t)) soit une base directe. Ainsi, toute courbe de Jordan d'un plan orienté est naturellement orientée.
Orientation de l'espace de dimension trois
Orienter l'espace consiste également à choisir une base directe arbitraire. On respecte généralement la règle des trois doigts de la main droite. Un plan et une droite perpendiculaires peuvent être orientés corrélativement. Les règles du bonhomme d'Ampère et du tire-bouchon de Maxwell sont utilisés par les physiciens pour expliquer intuitivement ce que signifie orienter l'espace.
Si cette convention est choisie, alors on a concrètement :
- Le sens direct de l'espace correspond au mouvement d'une vis que l'on visse dans une plaque de bois ;
- Son sens indirect correspondant alors au mouvement de la vis que l'on dévisse de cette plaque de bois.
L'orientation d'un espace vectoriel euclidien de dimension 3 autorise l'introduction du produit vectoriel. L'orientation intervient dans le choix du sens du vecteur
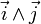 .
.Espace vectoriel complexe
Un espace vectoriel complexe E de dimension finie est, en tant qu'espace vectoriel réel, naturellement orienté. Plus exactement, si e=(e1,...,en) est une base complexe de E, alors e' = (e1,e2,...,en,i.e1,i.e2,...,i.en) est une base vectorielle réelle de E. Si M est la matrice de passage entre deux bases complexes e et f, alors la matrice de passage entre les bases complexes correspondantes est :
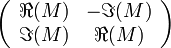 .
.
Son déterminant est | det(M) | 2. Etant positif, les bases e' et f' définissent les mêmes orientations de E.
Orientation d'une surface
La définition de l'orientation d'une surface dépend de la manière de regarder cette surface (points de vue intrinsèque ou extrinsèque).
Une orientation d'une surface S est la donnée d'orientations de ses plans tangents TMS, et qui en un sens à préciser sont compatibles. Si ce plan tangent peut se réaliser comme un plan vectoriel de R3, le choix d'une orientation se résume au choix d'une orientation sur l'orthogonal, qui est une droite vectorielle. La définition de l'orientation des surfaces plongées dans R3 est dont particulière.
Une surface S de R3 est dite orientable lorsqu'il existe une application continue n:S
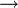 R3 telle que, en chaque point M de la surface S, le vecteur n(M) est non nul et orthogonal au plan tangent TMS. Une telle application n est appelée champ de vecteurs normaux de S. Deux tels champs n et m définissent la même orientation de S lorsque, en tout point M de S, n(M), et m(M) sont positivement colinéaires. On définit ainsi une relation d'équivalence sur les champs de vecteurs normaux, et les classes d'équivalence sont les orientations de S. Lorsque S est connexe, il existe exactement deux orientations distinctes.
R3 telle que, en chaque point M de la surface S, le vecteur n(M) est non nul et orthogonal au plan tangent TMS. Une telle application n est appelée champ de vecteurs normaux de S. Deux tels champs n et m définissent la même orientation de S lorsque, en tout point M de S, n(M), et m(M) sont positivement colinéaires. On définit ainsi une relation d'équivalence sur les champs de vecteurs normaux, et les classes d'équivalence sont les orientations de S. Lorsque S est connexe, il existe exactement deux orientations distinctes.Orienter la surface orientable connexe, c'est choisir une des deux orientations.
Les définitions se généralisent directement pour les hypersurfaces de Rn.
Il faut savoir que toute hypersurface compacte de Rn est orientable : cette propriété est une généralisation du théorème de Jordan en dimension >2.
Orientabilité et orientation pour une variété
Considérons une variété topologique de dimension n. Étant donnée une orientation de Rn, chaque carte permet d'orienter le morceau de la variété qu'il décrit. Toutefois, pour la variété prise globalement, il n'y pas de raison pour que les graphes se recouvrant voient leur orientation s'accorder. Les variétés, telles que la sphère, où les différents graphes peuvent être choisis pour que les régions se recouvrant s'accordent sur leur orientation, sont appelées variétés orientables. En topologie différentielle, une des façons de définir cette notion d'orientabilité et d'orientation est d'introduire la forme volume.
Le bord d'une variété orientée est une variété orientée sans bord. Cette remarque conduit à une formulation du cobordisme pour les variétés orientées sans bord.
On peut citer quelques exemples de variétés non orientables : (1) l'anneau de Möbius, qui est une variété avec bords, (2) la bouteille de Klein et (3) le plan projectif réel qui apparaît naturellement en géométrie. Des constructions topologiques de ces surfaces sont proposées dans les articles dédiés.
Approche homologique de l'orientation
Une orientation d'un espace topologique est la donnée d'un générateur ex du groupe Hn(X,X-x,Z) pour tout point x de X, et de sorte que, pour tout point x, il existe un voisinage compact Vx et d'un élément u de Hn(X,X-Vx,Z) dont la restriction dans Hn(X,X-y) est ey pour tout y.
Un espace topologique est dit orientable s'il admet au moins une orientation. S'il est connexe et orientable, il admet exactement deux orientations.
Les exemples les plus simples d'espaces topologiques orientables sont les espaces discrets. Une orientation se résume essentiellement à un choix de signes + ou - associés à chaque point de l'ensemble, sans contraintes. L'ensemble des orientations d'un espace discret X est de cardinal 2|X|.
Une variété est orientable si et seulement si l'espace topologique sous-jacent est orientable. Les définitions d'orientation se correspondent parfaitement.
Orientation et notions physiques
Le choix d'une orientation de l'espace mathématique permet de distinguer les notions physiques dépendant de ce choix des notions n'en dépendant pas. Les notions physiques dépendant d'un choix de l'orientation sont essentiellement celles qui utilisent le produit vectoriel.
Le moment cinétique, le moment dynamique, le moment d'une force, le couple de forces, le rotationnel, le champ magnétique, le nord et le sud, sont des notions dépendant de l'orientation de l'espace. On appelle vecteur axial ou pseudovecteur un vecteur dépendant de l'orientation. Un tel vecteur est changé en son opposé si on change d'orientation (i.e. si on intervertit droite et gauche).
L'orthogonalité, le gradient, la divergence, le champ électrique, la vitesse d'un point mobile, son accélération, sont des notions ne dépendant pas de l'orientation de l'espace. On appelle vecteur polaire un vecteur ne dépendant pas de l'orientation. Un tel vecteur reste invariant si on change d'orientation.
On dispose des relations suivantes entre vecteurs polaires et vecteurs axiaux.
- Vecteur axial = Vecteur polaire
 Vecteur polaire
Vecteur polaire - Vecteur polaire = Vecteur polaire
 Vecteur axial
Vecteur axial - Vecteur axial = Vecteur axial
 Vecteur axial
Vecteur axial - Rotationnel(Vecteur polaire) = Vecteur axial
- Rotationnel(Vecteur axial) = Vecteur polaire
Notes
- Portail des mathématiques
Catégories : Déterminant | Géométrie
Wikimedia Foundation. 2010.