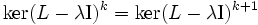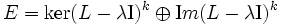Operateur compact

En analyse, un opérateur compact (ou application compacte ou encore opérateur complètement continu) est une application linéaire A entre deux espaces vectoriels topologiques localement convexes X et Y envoyant les parties bornées de X sur les parties relativement compactes de Y. Les applications compactes généralisent les applications linéaires continues de rang fini, qui en sont des cas particuliers. L'étude relève de l'analyse fonctionnelle à proprement parler.

La théorie est particulièrement intéressante pour les espaces vectoriels normés ou les espaces de Banach. En particulier, dans un espace de Banach, l'ensemble des opérateurs compacts est fermé pour la topologie forte. Mieux, dans un espace de Hilbert, un opérateur compact est la limite d'opérateurs de rang fini. Cette dernière propriété n'est pas vérifiée dans certains espaces de Banach.

Les premiers opérateurs compacts sont apparus avec les équations intégrales et l'étude des espaces fonctionnels. La résolution formelle d'équations intégrales simples font apparaître un opérateur à noyau dont la compacité tient à des propriétés d'équicontinuité. À travers ce problème est apparu une autre classe importante d'opérateurs, les opérateurs de Fredholm. La perturbation par des opérateurs compacts préserve la propriété d'être de Fredholm et l'indice de Fredholm : c'est le théorème de stabilité de l'indice.

Sommaire 1 Définition 2 Exemples 2.1 Opérateurs de rang fini 2.2 Opérateurs à noyau 2.3 Opérateurs compacts dans les espaces de Hilbert 3 Spectre des opérateurs compacts 4 Voir aussi 4.1 Articles connexes 4.2 Bibliographie

Définition

Dans un espace vectoriel topologique localement convexe séparé (evtlcs) X, une partie de X est dite bornée lorsqu'elle est incluse dans k.V pour tout voisinage V de 0 avec k suffisamment grand. Un opérateur T de X dans Y est dit compact lorsque toute partie bornée de X est envoyée sur une partie compacte de Y.

La somme de deux opérateurs compacts ou le produit d'un opérateur compact par un scalaire est encore un opérateur compact. L'ensemble K(X,Y) des opérateurs compacts de X dans Y forme donc un sous-espace vectoriel réel de L(X,Y). En outre, le composé d'un opérateur borné et d'un opérateur compact est un opérateur compact. En particulier, K(X)=K(X,X) est un idéal bilatère de L(X). Il est possible d'introduire la structure quotient L(X) / K(X), appelée algèbre de Calkin.

Si la topologie de X est définie par une norme, les parties bornées de X sont exactement celles incluses dans une boule. Sous cette condition, un opérateur T est compact ssi la boule unité de X soit envoyée sur une partie relativement compacte de Y. De manière équivalente, on demande à ce que, pour toute suite bornée x_n de X, la suite T'x_n admette une valeur d'adhérence.

Exemples

Opérateurs de rang fini

Opérateurs à noyau

Opérateurs compacts dans les espaces de Hilbert

Spectre des opérateurs compacts

Comme précédemment, on considère un opérateur compact L, endomorphisme de l'espace de Banach X sur le corps des complexes. Le spectre de L est lui-même compact, au plus dénombrable, et ne comportant aucun point d'accumulation, à l'exception éventuelle de 0. Il s'agit donc

• soit d'un ensemble fini contenant 0 ;
• soit d'un ensemble infini contenant 0. Dans ce cas les éléments du spectre autres que 0 peuvent être ordonnés en une suite vérifiant

et de limite nulle.

Notamment, pour un réel δ > 0 donné, il n'y a qu'un nombre fini d'éléments λ appartenant au spectre et de module supérieur à δ.

Les complexes 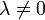appartenant au spectre jouissent de propriétés communes car l'opérateur L − λI est alors de Fredholm, d'indice 0. Notamment les éléments λ du spectre autres que 0 sont tous des valeurs propres, c'est-à-dire que L − λI est non injectif. Et la dimension du noyau L − λI est finie, égale à la codimension de l'image.

Il est possible de définir la multiplicité algébrique de ces valeurs propres : c'est le plus petit entier k tel que

pour cette valeur de l'entier k, on a la somme directe

l'opérateur L − λI induisant sur le premier espace un endomorphisme nilpotent, sur le second une bijection.

Quant à l'élément 0 du spectre, il peut s'agir ou non d'une valeur propre.

Voir aussi

Articles connexes

• Opérateur borné
• Opérateur de Fredholm

Bibliographie

• Walter Rudin, Analyse fonctionnelle [détail des éditions]

• Portail des mathématiques