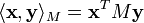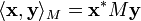- Matrice Définie Positive
-
Matrice définie positive
En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif.
On introduit tout d'abord les notations suivantes ; si a est une matrice à éléments réels ou complexes :
- aT désigne la transposée de a
- a * désigne la matrice transconjuguée de a (conjuguée de la transposée)
On rappelle que :
 désigne le corps des nombres réels
désigne le corps des nombres réels désigne le corps des nombres complexes
désigne le corps des nombres complexes
Sommaire
Matrice symétrique réelle définie positive
Soit M une matrice symétrique réelle d'ordre n. Elle est dite définie positive si elle vérifie l'une des 3 propriétés équivalentes suivantes :
1. Pour toute matrice colonne non nulle 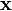 à n éléments réels, on a
à n éléments réels, on a
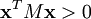 .
.
(autrement dit, la forme quadratique définie par
 est strictement positive pour
est strictement positive pour 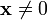 )
)2. Toutes les valeurs propres de M sont strictement positives, c'est-à-dire : ![\ \mathrm{sp}(M) \subset\, ]0,\, +\infty[\,](/pictures/frwiki/55/72bacc4282291424eb1bfc3ffecdb90e.png) .
.
3. La forme bilinéaire symétrique définie par la relation est un produit scalaire sur
 (identifié ici à l'espace vectoriel des matrices colonnes à n éléments réels).
(identifié ici à l'espace vectoriel des matrices colonnes à n éléments réels).Une matrice symétrique réelle est dite définie négative si son opposée (symétrique elle aussi) est définie positive.
La propriété 1 signifie que M définit sur
 une forme quadratique définie positive, la propriété 2 que sur
une forme quadratique définie positive, la propriété 2 que sur  , vu comme espace euclidien avec le produit scalaire
, vu comme espace euclidien avec le produit scalaire 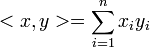 , M définit un opérateur auto-adjoint positif. L'équivalence entre 1 et 2 vient de cette double interprétation, à la lumière de la réduction de Gauss et du théorème spectral. Si 1 est vraie, sachant que les valeurs propres d'une matrice symétrique réelle sont réelles, on voit en appliquant 1 aux vecteurs propres que les valeurs propres sont strictement positives. Si 2 est vraie, il existe une matrice orthogonale
, M définit un opérateur auto-adjoint positif. L'équivalence entre 1 et 2 vient de cette double interprétation, à la lumière de la réduction de Gauss et du théorème spectral. Si 1 est vraie, sachant que les valeurs propres d'une matrice symétrique réelle sont réelles, on voit en appliquant 1 aux vecteurs propres que les valeurs propres sont strictement positives. Si 2 est vraie, il existe une matrice orthogonale 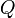 telle que
telle que 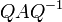 soit diagonale (parce que
soit diagonale (parce que  est symétrique réelle) à coefficients diagonaux strictement positifs (c'est l'hypothèse 2 sur les valeurs propres). Mais comme Q − 1 = tQ, la matrice
est symétrique réelle) à coefficients diagonaux strictement positifs (c'est l'hypothèse 2 sur les valeurs propres). Mais comme Q − 1 = tQ, la matrice  est aussi congrue à la matrice diagonale en question, donc la forme quadratique
est aussi congrue à la matrice diagonale en question, donc la forme quadratique 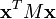 est définie positive.
est définie positive.Exemple de base
Pour toute matrice réelle
 , les matrices symétriques
, les matrices symétriques 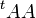 et
et 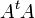 sont positives ; elles sont définies positives si et seulement si
sont positives ; elles sont définies positives si et seulement si  est inversible. Les matrices de Gram donnent un exemple de cette situation.
est inversible. Les matrices de Gram donnent un exemple de cette situation.Exemple : matrice de Hilbert
On appelle matrice de Hilbert la matrice (symétrique d'ordre n)
 , telle que
, telle que 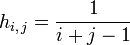 . Elle est définie positive.
. Elle est définie positive.- En effet, soit une matrice colonne quelconque
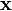 à n éléments réels
à n éléments réels 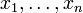 .
. - On remarque que
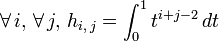 . Alors, par linéarité de l'intégrale :
. Alors, par linéarité de l'intégrale : 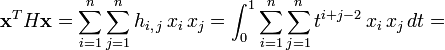
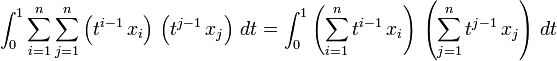 ,
,- d'où enfin :
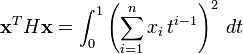 .
. - Dans cette dernière intégrale, l'intégrande est continu et à valeurs positives. Par conséquent :
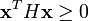 ;
;- si
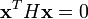 , alors pour tout
, alors pour tout ![t \in\, [0,\, 1],\, \left(\sum_{i = 1}^nx_i\, t^{i - 1}\right)^2 = 0](/pictures/frwiki/57/96cce4f327d06e4b1a2d5b320cf8b599.png) .
.
- Donc pour tout
![t \in\, [0,\, 1],\, \sum_{i = 1}^nx_i\, t^{i - 1} = 0](/pictures/frwiki/100/da2dbaf428a077efc68b426d5caedf63.png) .
. - Il en résulte que les
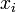 , coefficients d'un polynôme admettant une infinité de racines, sont tous nuls, c'est-à-dire
, coefficients d'un polynôme admettant une infinité de racines, sont tous nuls, c'est-à-dire 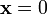 .
.
- Ceci prouve que
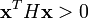 pour toute matrice colonne non nulle
pour toute matrice colonne non nulle 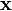 à n éléments réels.
à n éléments réels.
Nota : ceci est un cas particulier d'une propriété des matrices de Gram. La matrice de Gram d'une famille de n vecteurs d'un espace préhilbertien (réel ou complexe) est définie positive si et seulement si la famille est libre.
Matrice hermitienne définie positive
On étend les propriétés et définitions précédentes aux matrices complexes hermitiennes.
Soit M une matrice hermitienne d'ordre n. Elle est dite définie positive si elle vérifie l'une des 3 propriétés équivalentes suivantes :
1. Pour toute matrice colonne non nulle  à n éléments complexes, on a
à n éléments complexes, on a
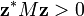 .
.
2. Toutes les valeurs propres de M sont strictement positives, c'est-à-dire : ![\ \mathrm{sp}(M) \subset\, ]0,\, +\infty[\,](/pictures/frwiki/55/72bacc4282291424eb1bfc3ffecdb90e.png) .
.
3. La forme sesquilinéaire définie par la relation est un produit scalaire sur
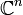 (identifié ici à l'espace vectoriel des matrices colonnes à n éléments complexes).
(identifié ici à l'espace vectoriel des matrices colonnes à n éléments complexes).Une matrice hermitienne est dite définie négative si son opposée (hermitienne elle aussi) est définie positive.
Propriétés
Les propriétés suivantes sont communes aux matrices symétriques réelles et aux matrices complexes hermitiennes.
- Toute matrice définie positive est inversible (à déterminant réel strictement positif), et son inverse est elle aussi définie positive.
- Si M est définie positive et r est un nombre réel strictement positif, alors rM est définie positive.
- Si M et N sont définies positives, alors M + N est définie positive.
- Si M et N sont définies positives, et si MN = NM (on dit qu'elles commutent), alors MN est définie positive.
- Une matrice M est définie positive si et seulement s'il existe une matrice définie positive A telle que A2 = M ; dans ce cas, la matrice définie positive A est unique, et on peut la noter A = M1 / 2 (voir l'article racine carrée d'une matrice).
Cette propriété est utilisée pour la décomposition polaire.
Critère de Sylvester
Pour qu'une matrice
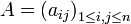 , réelle symétrique ou complexe hermitienne, soit définie positive, il faut et suffit que les les n matrices
, réelle symétrique ou complexe hermitienne, soit définie positive, il faut et suffit que les les n matrices 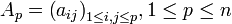 aient leur déterminant strictement positif, autrement dit que tous les mineurs principaux aient leur déterminant strictement positif.
aient leur déterminant strictement positif, autrement dit que tous les mineurs principaux aient leur déterminant strictement positif.
Remarque. Pour n=2, le critère de Sylvester est essentiellement le critère de positivité du trinôme du second degré.Preuve. La condition est nécessaire. On remarque d'abord que si la forme quadratique
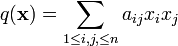 est définie positive, alors
est définie positive, alors  . En effet, par rapport à une base orthogonale pour cette forme quadratique (il en existe, d'après la réduction de Gauss), la matrice de q s'écrit
. En effet, par rapport à une base orthogonale pour cette forme quadratique (il en existe, d'après la réduction de Gauss), la matrice de q s'écrit  les
les 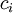 étant tous strictement positifs. Alors
étant tous strictement positifs. Alors  (Q étant la matrice de passage), donc
(Q étant la matrice de passage), donc  . Le résultat s'ensuit, en appliquant le même raisonnement à la restriction de q aux sous-espaces
. Le résultat s'ensuit, en appliquant le même raisonnement à la restriction de q aux sous-espaces  , pour
, pour 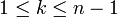 .
.Montrons maintenant que la condition est suffisante. On procède par récurrence sur la dimension. Pour n=1 c'est évident : alors
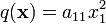 . Supposons la propriété vraie pour n-1. La forme
. Supposons la propriété vraie pour n-1. La forme 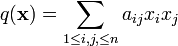 est non dégénérée (parce que
est non dégénérée (parce que 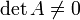 ) et sa restriction à
) et sa restriction à 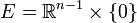 est définie positive (d'après l'hypothèse de récurrence). En particulier,
est définie positive (d'après l'hypothèse de récurrence). En particulier, 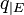 est non dégénérée, donc
est non dégénérée, donc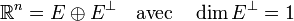
Soit
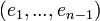 une base orthogonale pour
une base orthogonale pour 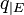 . En la complétant par un vecteur
. En la complétant par un vecteur 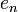 non nul de
non nul de 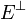 , on obtient une base orthogonale pour q. Soit
, on obtient une base orthogonale pour q. Soit 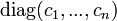 la matrice de q dans cette base. On sait déjà que
la matrice de q dans cette base. On sait déjà que 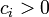 pour
pour 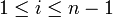 , puisque
, puisque 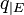 est définie positive. On sait aussi, d'après le même argument que dans la première partie (qui met implicitement en jeu le discriminant), que
est définie positive. On sait aussi, d'après le même argument que dans la première partie (qui met implicitement en jeu le discriminant), que 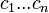 et
et 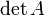 ont même signe. Ainsi
ont même signe. Ainsi 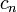 est lui aussi strictement positif, ce qui montre que q est définie positive.
est lui aussi strictement positif, ce qui montre que q est définie positive.Dans le cas complexe, la preuve est analogue, en considérant la forme hermitienne définie par la matrice.
Voir aussi
Articles de mathématiques en rapport avec l'algèbre bilinéaireEspace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz
- Portail des mathématiques
Catégories : Algèbre bilinéaire | Matrice remarquable
Wikimedia Foundation. 2010.