Caractere d'une representation d'un groupe fini

Caractère d'une représentation d'un groupe fini

Fichier:Ferdinand Georg Frobenius.jpg

Ferdinand Georg Frobenius fondateur de la théorie des caractères

En mathématiques le caractère d'une représentation d'un groupes finis est un outil utilisé pour analyser les représentations d'un groupe fini.

Le caractère d'une représentation (V, ρ) d'un groupe G correspond à l'application de G dans le corps de l'espace de la représentation qui à un élément s associe la trace de l'image de s par ρ.

Cette définition n'est pas compatible avec celle des caractères d'un groupe en général qui ne prend ses valeurs que dans l'ensemble des complexes différents de zéro.

L'utilisation du caractère d'une représentation d'un groupe fini est essentielle pour la classification des représentations. La somme directe de représentation possède pour caractère la somme des caractère et deux représentations irréductibles différentes possèdent des caractères orthogonaux.

Définitions

Le caractère χ_ρ de la représentation (V, ρ) est une application de G un groupe fini dans K le corps de la représentation qui à s associe la trace de ρ_s.

$\forall s \in g \quad \chi_{\rho}(s)=Tr(\rho_s)\;$

Un cas important correspond à celui où le corps K est égal à celui des nombres complexes.

Un exemple simple correspond au cas des représentations de dimension un. Il est alors possible d'identifier V à K. Le caractère apparaît comme un morphisme de groupe. Le théorème de Lagrange démontre que l'ensemble des images est inclus dans celui des racines g-ième de l'unité.

Un caractère irréductible est le caractère d'une représentation irréductible.

Contexte

Histoire

Les travaux de Jordan (1838-1922) avec la publication d'un livre^[1] sur les équations algébriques représente une première analyse d'un groupe fini de matrices représentant un groupe de Galois. Frobenius (1849 - 1917) démarre en 1896 l'étude de la théorie des caractères des groupes finis^[2], les caractères ne sont pas encore liés à la notion de représentation. Cette même année il communique, dans une lettre à Dedekind (1831-1916) les caractères des représentations irréductibles des groupes symétriques d'ordre quatre et cinq.

La théorie est rapidement développée, entre 1897 et 1899 la machinerie est mise en place. Frobenius développe le produit tensoriel, les représentations induites ainsi que son théorème de réciprocité. En 1900 il détermine les caractères des groupes symétriques et l'année suivante ceux des groupes alternés.durant cette époque, Heinrich Maschke (1853 1908) démontre le théorème portant maintenant son nom^[3] qui stipule que toute représentation d'un groupe fini est somme directe de représentations irréductibles.

William Burnside (1852-1927) comprend rapidement la profondeur des travaux de Frobenius. Il utilise la théorie des caractères pour montrer^[4] qu'un groupe d'ordre pⁿ.q^m si p et q sont premiers est un groupe résoluble. Il publie en 1911 la deuxième édition d'un livre de référence^[5]. Elle formalise en une théorie le savoir de l'époque sur les groupes finis, l'édition contient les travaux sur les caractères de Frobenius.

Un autre acteur important de la théorie Issai Schur (1875-1941) est un élève de Frobenius. Non seulement il travaille sur les aspects théoriques et démontre son lemme^[6], mais de plus, dans l'année 1925 il applique la théorie à la physique quantique.

La théorie est l'objet d'un large développement durant le XX^e siècle. On peut citer les travaux d'Artin (1898-1962) avec la notion de caractère virtuel, ceux de Richard Brauer (1901-1977) avec son théorème sur les combinaisons linéaires à coefficients entiers ou encore plus récemment Thompson né en1932 qui reçoit la Médaille Fields pour avoir démontré une vieille conjecture de Burnside annonçant que tout groupe fini d'ordre impair est résoluble.

Motivation

Le théorème de Maschke démontre que si un corps K est soit de caractéristique nulle soit première avec l'ordre du groupe G étudié alors toutes représentation sur un K-espace vectoriel est somme directe de sous-espaces irréductibles.

La théorie se concentre alors sur deux points clés : comment connaître les représentations irréductibles et comment, pour une représentation donnée connaître ses facteurs irréductibles. La théorie des caractères répond partiellement à la première des deux questions et totalement à la deuxième.

Introduction par l'exemple

Article détaillé : Représentations du groupe symétrique d'indice trois.

Représentation de S₃ comme groupe des isométries du triangle

Considérons le polynôme P[X] à coefficients dans les nombres rationnels Q défini par P[X] = X³ + X + 1. La théorie montre qu'il existe un espace vectoriel V sur Q de dimension six et que le groupe de Galois G opére sur V. Plus précisément, G est un groupe d'automorphismes de V isomorphe à S₃. La difficulté réside maintenant dans le fait que la dimension de l'espace est égale à six. Le groupe se représente par six matrices carrées 6x6. Ce qui rend le problème plus ardu.

Recherchons dans un premier temps toutes les représentations irréductibles. Il existe un premier cas aisé, celui où V est de dimension un et identifié à C et où le morphisme t associe à tout élément de S₃ la valeur un. On parle alors de représentation triviale. Un deuxième cas σ utilise le même espace V, il associe à tout élément de S₃ sa signature, c’est-à-dire -1 si la permutation est une transposition et 1 sinon.

Le troisième cas est illustré sur la figure de gauche. L'espace vectoriel est de dimension deux et le morphisme θ associe aux trois transpositions les symétries orthogonales d'axes ceux représentés en rouge sur la figure. Les deux éléments d'ordre trois sont alors les rotations d'angles 2.π/3 et -2.π/3.

La théorie des caractères montre qu'il n'existe pas d'autre représentation irréductible de ce groupe. Il existe deux manières de s'en rendre compte, soit par la représentation régulière qui montre que l'ordre (ici égal à 6) est égal à la somme des carrés des degrés des différentes représentations irréductibles ici égal à 1 + 1 + 4, soit par les fonctions centrales qui montre que le nombre de représentations irréductibles est égal aux nombre de classes de conjugaison du groupe. Une fonction centrale est une fonction du groupe constante sur les classes de conjugaison.

Caractères du groupe symétrique d'indice trois.

Remarquons que le groupe S₃ comporte trois classes de conjugaison, celle de l'unité, celle des trois transpositions T = {t₁, t₂, t₃} et celle des deux cycles d'ordre trois C = {c₁, c₂}. Il est relativement simple de vérifier que les trois caractères sont constants sur chaque classe de conjugaison, cette propriété est générale pour tous les caractères. De plus, il existe un produit scalaire (dans le cas général un produit hermitien) tel que les caractères irréductibles forment une base orthonormale. Ce résultat est au coeur de la théorie des caractères. Dans notre cas, si Si φ et ψ sont deux fonctions centrales il est donné par :

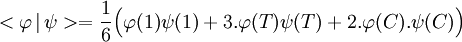
$< \varphi \, | \, \psi> = \frac 16 \Big( \varphi (1){\psi(1)} + 3.\varphi(T)\psi(T)+ 2.\varphi(C).\psi(C) \Big)$

Ces propriétés permettent simplement de factoriser l'exemple donné sur S₃. Notons χ_t,χ_σ, χ_θ les caractères des trois représentations irréductibles et χ_ρ le caractère de la représentation du groupe de Galois. Comme, la famille des caractères irréductibles est une base, il existe trois scalaires a, b et c tel que :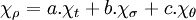

$\chi_{\rho}=a.\chi_{t}+b.\chi_{\sigma}+c.\chi_{\theta}\;$

Comme la base est orthonormée, les trois coefficients sont données par les formules :

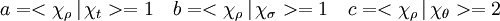
$a=<\chi_{\rho} \, | \, \chi_{t}>=1\quad b=<\chi_{\rho} \, |\, \chi_{\sigma}>=1\quad c=<\chi_{\rho} \, |\, \chi_{\theta}>=2 \;$

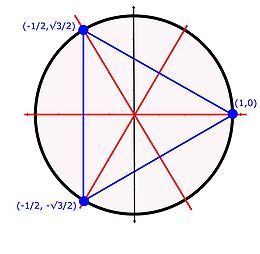
La figure de droite illustre les caractères du groupe S₃. Les caractères représentés par des boules orange sont les trois irréductibles, la boule bleu représente le caractère de la représentation de Galois. Elle est combinaison linaire des trois caractères irréductibles avec les coefficient un pour la triviale, un pour la signature et deux pour celle des isométries du triangle.

Premières propriétés

L'image de l'unité par un caractère est égale à la dimension n de V.

Cette propriété provient du fait que ρ₁ est égal à l'identité de V.

Si s et t sont deux éléments du groupe, alors st et ts ont même image par le caractère.

Cette propriété est une conséquence directe des propriétés de la trace : deux matrices semblables (c’est-à-dire qui représentent le même endomorphismes dans deux bases différentes ont même caractères).

Si deux représentations sont isomorphes alors elles ont même caractère.

Cette propriété se démontre comme la propriété précédente.

Si s et t sont deux éléments conjugués du groupe, c’est-à-dire s'il existe un élément u tel que usu^-1 = t, alors ils ont même image par le caractère.

La trace est invariante par changement de base. Si la matrice associée à ρ_u est considérée comme une matrice de passage, on constate que les images de s et t par ρ ont des matrices associées semblables.

Si le corps K est inclus dans celui des complexes et s un élément du groupe, alors l'image de s^-1 par le caractère est le conjugué de l'image de s.

L'endomorphisme ρ_s possède comme polynôme annulateur X^g - 1 d'après le théorème de Lagrange. Son polynôme minimal est scindé, car le corps est algébriquement clos et séparable c’est-à-dire qu'il n'admet pas de racine multiple (cf polynôme cyclotomique). En conséquence l'endomorphisme est diagonalisable. Chaque valeur propre λ est une racine de l'unité et admet pour inverse sa valeur conjuguée. En conséquence l'image par ρ de s^-1, égal à l'inverse de ρ_s et est diagonalisée dans la même base avec pour valeur sur la diagonale les conjuguées de celle de ρ_s, ce qui démontre la proposition. Ces propriétés ne sont pas spécifiques aux caractère fini des groupes. On obtient le corollaire suivant :

Si le corps K est inclus dans celui des réels et s un élément du groupe, alors l'image de s^-1 par le caractère est la même que celle de s.

Cette propriété se généralise au cas où le corps est de caractéristique finie p s'il est algébrique. La théorie de Galois démontre l'existence d'un automorphisme φ de corps laissant stable l'extension de dimension deux du corps premier F_p (cf corps fini). L'application φ joue le rôle d'application conjuguée. φ² est égale à l'identité et si x est un élément de K, x.φ(x) est un élément du corps premier (celui engendré par 1). Si λ est une racine g-ième de l'unité alors λ.φ(λ) est un élément du corps premier dont la puissance g est égal à un. Comme g est premier avec p, la caractéristique du corps, λ.φ(λ) est égal à un et φ(λ) est égal à λ_-1. En conséquence l'image de s^-1 par le caractère est égal à φ(χ_s).

Exemple

Les caractères d'un groupe sont parfois donnés sous forme de table. Comme un caractère est constant sur une classe de conjugaison, la table est ainsi donné sur les classes de conjugaison. Celle du groupe alterné de degré 4 est par exemple :

Car. irr.	1	(ab)(cd)	(abc)	(acb)
t	1	1	1	1
σ₁	1	1	j	j²
σ₂	1	1	j²	j
φ	3	-1	0	0

Un élément du type (ab)(cd) possède son inverse dans la même classe de conjugaison, la valeur du caractère est toujours réelle pour cette classe. En revanche, l'inverse de (abc) est (acb), les deux valeurs sont toujours conjuguées. Cette table est calculée dans l'article groupe alterné.

Orthogonalité

Lemme de Schur

Article détaillé : Lemme de Schur.

Le théorème de Maschke donne une importance particulière aux représentations irréductibles. En effet, toute représentations est somme directe de représentations irréductibles.

Soit deux représentations irréductibles (V₁, ρ¹) (V₂, ρ²) de caractères respectifs χ₁ et χ₂. Les caractères sont des éléments de l'espace vectoriel C des applications de G dans K. Soient M¹ = (m¹_ij) et M² = (m²_kl) les représentations sous forme matricielles de ρ¹ et ρ². On dispose des relations suivantes :

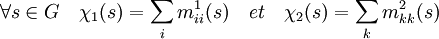
$\forall s \in G\quad \chi_1(s)=\sum_{i} m_{ii}^1(s) \quad et \quad \chi_2(s)=\sum_{k} m_{kk}^2(s) \;$

En vue d'appliquer le corollaire 4 du lemme de Schur il est nécessaire de supposer que le corps K est de caractéristique soit nulle soit première avec g l'ordre du groupe et que le polynôme X^g - 1 est scindé dans K. On dispose alors des deux propriétés suivantes :

(1) Si les représentations ρ¹ et ρ² ne sont pas isomorphes, alors :

$\forall i,j \in [1,n_1] \; \forall k,l \in [1,n_2] \quad \sum_{s\in G} m_{ij}^1(s).m_{kl}^2(s^{-1})=0$

(2) Si les deux représentations sont isomorphes, alors :

$\forall i,j,k,l \in [1,n_1] \quad \frac{1}{g}\sum_{s\in G} m^1_{ij}(s).m^1_{kl} (s^{-1})=\frac{1}{n}\delta_{il}\delta_{jk}$

Où δ_ij désigne le symbole de Kronecker. Les démonstrations sont données dans l'article associé.

Caractéristique nulle

On suppose que le corps K est de caractéristique nulle et que le polynôme X^g - 1 est scindé dans K. Alors si l'on définit le produit hermitien suivant :

Le produit hermitien canonique < | > de l'espace C des fonctions du groupe G à valeur dans K est donnée par la formule suivante :

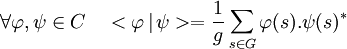
$\forall \varphi, \psi \in C \quad <\varphi \, |\,\psi> = \frac 1g\sum_{s \in G} \varphi(s).\psi (s)^*$

Ici, si a est un élément de K a^* désigne le conjugué de a. La définition permet d'exprimer la proposition suivante :

Si χ₁ et χ₂ sont deux caractères irréductibles, soit les représentations associées sont isomorphes et <χ₁ | χ₂> = 1, soit elles ne le sont pas et <χ₁ | χ₂> = 0.

On peut exprimer cette dernière proposition par :

La famille des caractères irréductibles est orthonormale.

En effet, l'expression du produit hermitien prend la forme suivante :

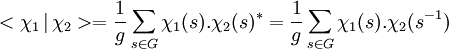
$<\chi_1 \, | \, \chi_2>= \frac 1g\sum_{s \in G} \chi_1(s).\chi_2 (s)^*= \frac 1g\sum_{s \in G} \chi_1(s).\chi_2 (s^{-1})$

La dernière égalité provient du fait que le caractère d'un inverse est le conjugué d'un caractère (cf Premières propriétés). En terme matricielle cette égalité se traduit par :

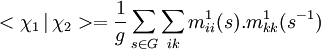
$<\chi_1 \, | \, \chi_2>= \frac 1g\sum_{s \in G}\sum_{ik} m_{ii}^1(s).m_{kk}^1(s^{-1})$

Le corollaire 4 du lemme de Schur permet de conclure.

Exemple

Article détaillé : Groupe simple d'ordre 168.

Il n'existe qu'un unique groupe simple d'ordre 168, il n'est pas abélien et correspond au deuxième groupe simple non commutatif, si ces groupes sont ordonnés à l'aide de leur ordre. On trouve la table suivante, établie dans l'article détaillé :

Car. irr.	C₁	C₂	C₃	C₄	C_7a	C_7b
χ₁	1	1	1	1	1	1
χ_3a	3	-1	0	1	1/2.(-1 + i√7)	1/2.(-1 - i√7)
χ_3b	3	-1	0	1	1/2.(-1 - i√7)	1/2.(-1 + i√7)
χ₆	6	2	0	0	-1	-1
χ₇	7	-1	1	-1	0	0
χ₈	8	0	-1	0	1	1

Les cardinaux des classes de conjugaisons sont C₁ : 1, C₂ : 21, C₃ : 56, C₄ : 42, C_7a : 24, C_7b : 24. On en déduit le produit hermitien pour deux caractères χ_φ et χ_ψ, dans le cas d'une représentation complexe :

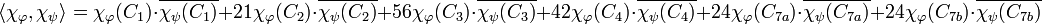
$\langle \chi_{\varphi} , \chi_{\psi}\rangle = \chi_{\varphi}(C_1)\cdot \overline{\chi_{\psi}(C_1)} + 21\chi_{\varphi}(C_2)\cdot \overline{\chi_{\psi}(C_2)} + 56\chi_{\varphi}(C_3)\cdot \overline{\chi_{\psi}(C_3)} + 42\chi_{\varphi}(C_4)\cdot \overline{\chi_{\psi}(C_4)} + 24\chi_{\varphi}(C_{7a})\cdot \overline{\chi_{\psi}(C_{7a})} + 24\chi_{\varphi}(C_{7b})\cdot \overline{\chi_{\psi}(C_{7b})}$

Les caractères de la table sont bien tous de norme 1 et orthogonaux deux à deux.

Conséquences

Cette propriété d'orthogonalité entraine des conséquences théoriques immédiates :

Soient (V, ρ) une représentation d'un groupe fini G, (V_i) une décomposition de V en sous-espaces irréductibles et (W, σ) une représentation irréductible de G. La représentation ρ_i désigne la restriction de ρ à V_i, χ désigne le caractère de ρ et ψ celui de σ. Le nombre de sous-espaces V_j de la famille (V_i) tel que (V_j, ρ_j) soit isomorphe à (W, σ) est égal à <χ|ψ>.

En effet, il suffit de remarquer que le caractère d'une somme directe est égal à la somme des caractères. L'orthogonalité des représentations irréductibles permet de conclure.

On en déduit les corollaires suivants :

La norme d'un caractère par le produit hermitien canonique est égale à un entier.

Un caractère est irréductible si et seulement si sa norme par le produit hermitien canonique est égal à un.

Représentation régulière

Article détaillé : Représentation régulière.

Il existe une représentation qui possède toutes représentations irréductibles comme sous-représentations, elle est appelée représentation régulière. Le théorème de Cayley montre que le groupe G est isomorphe à un sous-groupe du groupe symétrique d'ordre g. Si V est un K espace vectoriel de dimension G, il est possible d'indexer une base B de V par G. Le groupe G opère transitivement sur B. L'unique prolongement linéaire de l'action de groupe à V est une représentation, elle est dite régulière. C'est une représentation de degré g égal à l'ordre du groupe. Elle vérifie la propriété suivante :

La représentation régulière (V, ρ) de G est fidèle.

C’est-à-dire qu'elle est injective (cf théorie des représentations d'un groupe fini).

Sous réserve que les caractères irréductibles forment une famille orthonormale de K^G, alors si (W, σ) est une représentation irréductible de G de degré d :

Il existe exactement d sous-espaces invariants W_i de V, d'intersection nulle deux à deux, tel que la restriction de ρ, la représentation régulière, à W_i soit isomorphe à (W, σ).

Cette décomposition n'est pas unique. Le nombre de sous-espaces isomorphes à W de V est en général supérieur à d, mais il ne sont pas en somme directe. Il existe néanmoins une unique décomposition de la représentation régulière.

Il existe un unique sous-espace maximal S_W de V contentant tous les sous-espaces isomorphe à W. Il est appelé composante isotypique de W dans V. Les composantes isotypiques sont en somme directe égal à V.

Sous reserve des mêmes hypothèses que précédemment, si (W_j, σ_j) est l'ensemble des représentations irréductibles de G quand j varie de 1 à h, alors l'égalité suivante est vérifiée :

Soit d_j le degré de la représentation irréductible (W_j, σ_j) et g l'ordre de groupe, alors :

$\sum_{i=1}^h d_j^2=g$

Les démonstrations sont données dans l'article associé.

Ces propriétés sont utilisées, par exemple pour établir la table des caractères du groupe alterné d'indice 4 et 5, ou encore du groupe simple d'ordre 168.

Fonction centrale

Article détaillé : Fonction centrale d'un groupe fini.

Une fonction centrale est une application constante sur chaque classe de conjugaison du groupe. Les premières propriétés des caractères montrent que ce sont des fonctions centrales. Dans le cas où ils forment une famille orthonormale, alors :

Les caractères irréductibles forment une base orthonormale de l'espace vectoriel des fonctions centrales à valeur dans K.

On en déduit que :

Si h désigne le nombre de classes de conjugaison de G alors il existe h représentations irréductibles distinctes à un isomorphisme près.

Extension

Produit direct et produit tensoriel

Article détaillé : Produit tensoriel et représentations de groupes finis.

En théorie des groupes, la première méthode d'extension est donnée par le produit direct de deux groupes. En termes de représentation, cette extension se traduit par un produit tensoriel de deux représentations de deux groupes.

La relation entre une somme directe de représentations et ses caractères est donnée par la proposition suivante :

Le caractère de la somme directe de deux représentations (V, ρ) et (V',ρ') d'un groupe G est la somme des caractères des deux représentations.

En effet, si s est un élément de G, R_s et R_s' les matrices de ρ_s et ρ'_s dans des bases B et B' ,alors la réunion des deux bases est une base de V $\oplus$ V'. Dans cette base, la matrice S_s de ρ $\oplus$ ρ'_s prend la forme :

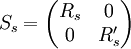
$S_s=\begin{pmatrix} R_s & 0 \\ 0 & R'_s \end{pmatrix}$

L'égalité sur les caractères, vu comme trace des matrices est alors évidente.

Cette proposition se généralise par récurrence au cas d'une somme directe d'un nombre fini de représentations.

Une relation analogue existe pour le produit tensoriel de représentations :

Le caractère du produit tensoriel de deux représentations (V, ρ) et (V',ρ') d'un groupe G est le produit des caractères des deux représentations.

En utilisant les notations précédentes et si (r_ij) (resp. (r'_i'j') est la matrice R_s (resp. R_s') la matrice P_s du produit tensoriel associée est égal à (p_{ij i'j'}) avec p_{ij i'j'} = r_ij.r'_i'j'. Un simple calcul de trace permet de conclure.

Si χ_σ (resp. χ_α) désigne le caractère de la représentation du carré symétrique (resp. alterné), alors les deux formules suivantes s'appliquent :

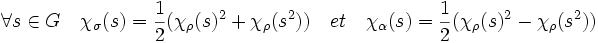
$\forall s \in G \quad \chi_{\sigma}(s)=\frac{1}{2}(\chi_{\rho}(s)^2 + \chi_{\rho}(s^2))\quad et \quad \chi_{\alpha}(s)=\frac{1}{2}(\chi_{\rho}(s)^2 - \chi_{\rho}(s^2)) \;$

Les définitions des représentations du carré symétrique et alterné sont données dans l'article détaillé.

Produit semi-direct et représentation induite

Article détaillé : Représentation induite d'un groupe fini.

Une représentation induite est un mode de construction d'une représentation d'un groupe G à l'aide d'un de ses sous-groupes H. Soit (W, θ) une représentation de H, une représentation (V, ρ) est dite induite par celle de (W, θ) si et seulement si les différents sous-espaces ρ_cW où les valeurs de c forment un système de représentants des classes à gauche de G/H, sont, en somme directe, égale à V.

Il existe une unique représentation induite de G par une représentation (W, θ) d'un sous-groupe H. En termes de G-module, la représentation induite s'exprime simplement :

$V\simeq K[G]\otimes_{K[H]}W \;$

La représentation induite correspond, en termes de G-module à une extension des scalaires K[H] à l'anneau K[G] sur le H-module W.

Dans le cas où H est un sous-groupe normal de G, la représentation induite est équivalente à un produit semi-direct.

Il existe un méthode simple pour calculer le produit hermitien du caractère d'une représentation induite : la formule de réciprocité de Frobenius Si ψ désigne le caractère de la représentation θ de H et χ celui d'une représentation de G, si Ind ψ désigne le caractère d'une représentation induite et Res χ le caractère de la restriction de ρ à H, alors :

$<Ind_H^G\,\psi\,|\,\chi>_G=<\psi\,|\,Res_H^G\,\chi>_H \;$

Notes et références

Articles sur les Représentations d'un groupe d'ordre fini

Notes

↑ Marie Ennemond Camille Jordan Traité des substitutions et des équations algébriques 1870
↑ Ferdinand Georg Frobenius, Sur le caractère du groupe, Académie de Berlin, 1896
↑ Heinrich Maschke Beweiss des Satzes, dass diejenigen endlichen linearen Substitutionesgruppen, in welchen einige durchgehends verschwindende Coefficienten auftenen intransitiv sind 1899
↑ William Burnside On the Representation of a Group of Finite Order as an Irreducible Group of Linear Substitutions and the Direct Establishment of the Relations Between the Group-Characteristics Proc. London Math. Soc. s2-1: 117-123 1904
↑ William Burnside Theory of Groups of Finite Order second edition Dover Publications Réédition de 2004
↑ Issai Schur Utersuchen uber dieDarstellung der endlichen Gruppen durch gebrochemen linearen Substitutionen J. Reine. Angew. Math., 132 p85 à 137 1907

Liens externes

(fr) Cours de représentation des groupes finis par M. Broué de l'université de Paris VII
(fr) Représentation linéaire des groupes finis, une introduction par D. Ferrand de l'université de Renne
(en) Références historiques Par le site de l'université de St Andrew

Références

Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]
(en) Marshall Hall, The theory of groups [détail des éditions]
Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
N. Bourbaki Algèbre, Chapitre VIII Paris, Hermann 1958

Portail des mathématiques

Ce document provient de « Caract%C3%A8re d%27une repr%C3%A9sentation d%27un groupe fini ».

Catégorie : Théorie des représentations

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Caractere d'une representation d'un groupe fini de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Caractère D'une Représentation D'un Groupe Fini — Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour analyser les représentations d un groupe fini.… … Wikipédia en Français
Caractère d'une représentation d'un groupe fini — En mathématiques le caractère d une représentation d un groupe fini est un outil utilisé pour analyser les représentations d un groupe fini. Le caractère d une représentation (V, ρ) d un groupe G correspond à l application de G dans le corps de l … Wikipédia en Français
Caractères d'une représentation d'un groupe fini — Caractère d une représentation d un groupe fini Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour … Wikipédia en Français
Théorie des caractères d'une représentation d'un groupe fini — Caractère d une représentation d un groupe fini Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour … Wikipédia en Français
Caractere d'un groupe fini — Caractère d un groupe fini En mathématiques, un caractère d un groupe fini est une notion associée à la théorie des groupes. Un caractère d un groupe fini G est un morphisme du groupe G dans C* le corps des nombres complexes non nuls. Ce concept… … Wikipédia en Français
Caractère D'un Groupe Fini — En mathématiques, un caractère d un groupe fini est une notion associée à la théorie des groupes. Un caractère d un groupe fini G est un morphisme du groupe G dans C* le corps des nombres complexes non nuls. Ce concept permet de définir le groupe … Wikipédia en Français
Caractère d'un groupe fini — En mathématiques, un caractère d un groupe fini est une notion associée à la théorie des groupes. Un caractère d un groupe fini G est un morphisme de groupes de G dans le groupe multiplicatif ℂ* des nombres complexes non nuls. Ce concept permet… … Wikipédia en Français
Théorie des caractères d'un groupe fini — Caractère d une représentation d un groupe fini Fichier:Ferdinand Georg Frobenius.jpg Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques le caractère d une représentation d un groupes finis est un outil utilisé pour … Wikipédia en Français
Representations d'un groupe fini — Représentations d un groupe fini En mathématiques, un groupe est une structure algébrique dont la définition est remarquablement simple. Elle consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle… … Wikipédia en Français
Représentations d'un groupe fini — En mathématiques, un groupe est une structure algébrique qui consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle est associative, il existe un élément neutre et tout élément admet un inverse. Un … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Caractere d'une representation d'un groupe fini

Caractère d'une représentation d'un groupe fini

Sommaire

Définitions