- Orthocentre
-
Triangle
 Pour les articles homonymes, voir Triangle (homonymie).
Pour les articles homonymes, voir Triangle (homonymie).En géométrie euclidienne, un triangle est une figure plane, formée par trois points et par les trois segments qui les relient. La dénomination de « triangle » est justifiée par la présence de trois angles dans cette figure, ceux formés par les segments entre eux. Les trois points sont les sommets du triangle, les trois segments ses côtés, et les trois angles ses angles.
Le triangle est une figure géométrique élémentaire, à l'instar du point, de la droite ou du cercle. Il constitue depuis l'Antiquité une réserve inépuisable de propriétés, d'exercices et de théorèmes mathématiques de difficultés variées. La plupart des propriétés et définitions énoncées dans cet article étaient déjà énoncées, environ 300 ans avant Jésus-Christ, dans les Éléments d'Euclide.
Pour l'étude du triangle dans d'autres géométries, voir Triangle (géométries non euclidiennes).
Sommaire
Conventions d'écriture
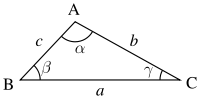
Les points intéressants d'une figure géométrique, tels les sommets d'un polygone, sont habituellement désignés par des lettres latines majuscules : ''A, B, C, ... Un triangle est alors nommé, comme tout autre polygone, en donnant successivement le nom de ses sommets, par exemple ABC. L'ordre de citation des sommets n'a pas d'importance, car tous les segments dont ces sommets sont les extrémités sont des côtés du triangle.
Les côtés du triangle, justement, sont dénommés, comme tous les segments, par leurs extrémités : AB, BC, et AC dans notre exemple. Pour nommer la longueur d'un côté, on utilise en général le nom du sommet opposé, converti en minuscule latine : a pour BC, b pour AC, c pour AB.
La notation générale pour l'angle entre deux segments OP et OQ partageant l'extrémité O est
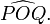
On peut aussi utiliser une lettre minuscule, grecque le plus souvent, surmontée d'un accent circonflexe (en toute rigueur, les grandeurs devraient être désignées par des majuscules et leur mesure par des minuscules, mais on recourt souvent aux mêmes noms pour les deux afin d'alléger les notations). Dans le cas d'un triangle, l'angle entre deux côtés peut encore, par tolérance et en l'absence d'ambiguïté, être désigné par le nom du sommet commun surmonté d'un accent circonflexe. Bref, dans notre exemple, nous pouvons noter les angles :
Si on tolère de confondre un angle et sa mesure dans les énoncés ou les calculs, la notation correcte est par exemple :
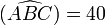 °.
°.
Nous utiliserons ces notations dans cet article.
Propriétés élémentaires
 Un tétraèdre
Un tétraèdre
Un triangle peut être défini comme un polygone à trois côtés, ou encore comme un polygone à trois sommets.
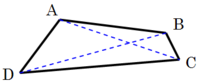
Après le point et le segment, le triangle est la figure polygonale la plus simple. C'est le seul qui ne possède pas de diagonale. Dans l'espace, trois points définissent un triangle (et un plan). A contrario, si quatre points coplanaires forment un quadrilatère, quatre points non coplanaires ne définissent pas un polygone, mais un tétraèdre :
D'autre part, tout polygone peut être découpé en un nombre fini de triangles qui forment alors une triangulation de ce polygone. Le nombre minimal de triangles nécessaire à ce découpage est n − 2, où n est le nombre de côtés du polygone. L'étude des triangles est fondamentale pour celle des autres polygones, par exemple pour la démonstration du théorème de Pick.
Longueurs des côtés et inégalité triangulaire
Dans un triangle, la longueur d'un côté est inférieure ou égale à la somme des longueurs des deux autres côtés. Autrement dit, dans un triangle ABC, les trois inégalités suivantes sont vérifiées :
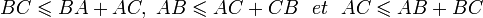
Cette propriété est caractéristique des triangles. Réciproquement, étant donnés trois nombres réels positifs a, b et c, si les trois inégalités :
sont vérifiées, alors il existe un triangle dont les côtés mesurent a, b et c.
Inversement, pour vérifier qu'il existe un triangle dont les longueurs des côtés sont a, b et c, il suffit en pratique de vérifier une seule des trois inégalités, celle où le plus long côté est à gauche de l'inégalité (ainsi, si max(a,b,c) = a , alors la seule inégalité à vérifier est :
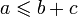 ).
).Le cas d'égalité de l'inégalité triangulaire permet de caractériser les points d'un segment : M est un point du segment [AB] si et seulement si : AM + MB = AB.
Enfin, la somme des longueurs des trois côtés d'un triangle est son périmètre.
Somme des angles
La somme des mesures des angles d'un triangle est égale à 180° ce qui équivaut à π radians.
Euclide avait démontré ce résultat dans ses Éléments (proposition I-32) de la manière suivante : traçons la parallèle à la droite (AB) passant par C. Étant parallèles, cette droite et la droite (AB) forment avec la droite (AC) des angles égaux, codés en rouge sur la figure ci-contre (angles alternes-internes). De la même façon, les angles codés en bleu sont égaux (angles correspondants). D'autre part, la somme des trois angles de sommet C est l'angle plat. Donc la somme des mesures d'un angle rouge, d'un angle vert et d'un angle bleu est 180° (ou π radians). La somme des mesures des angles du triangle est donc 180°.
Cette propriété est un résultat de géométrie euclidienne. Elle n'est pas vérifiée en général en géométrie non-euclidienne.
Typologie des triangles
Lorsque les trois sommets d'un triangle sont alignés, on parle de triangle aplati. Il est équivalent de dire qu'un angle du triangle est plat (il mesure alors 180°) ou que deux angles du triangle sont nuls (ils mesurent 0°).
Les triangles admettant deux angles droits (de 90°) et un angle nul (de 0°) sont qualifiés de triangles en aiguille (cas particulier de triangle aplati). C'est un cas limite, car les angles droits ne sont pas correctement définis.
Dans tous ces cas, on parle de triangles dégénérés. Dans la suite de cet article, on suppose que les triangles ne sont pas dégénérés. Dans le cas des triangles dégénérés, de nombreuses propriétés usuelles des triangles sont fausses ou triviales.
Classement selon le type d'angles
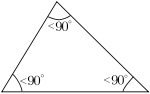
Comme la somme des angles d'un triangle vaut 180°, un triangle ne peut pas comporter deux angles droits (mesurant 90°) ou obtus (mesurant plus de 90°). Il a donc au moins deux angles aigus. Si le troisième angle est :
- droit, on parle de triangle rectangle ;
- obtus, on parle de triangle obtusangle ou ambligone (ou parfois de triangle obtus) ;
- aigu, on parle de triangle acutangle ou oxygone (ou de triangle aigu).
Classement suivant les symétries
Les triangles peuvent se classer suivant plusieurs types de symétries :
- suivant le nombre de côtés égaux ;
- suivant le nombre d'angles égaux ;
- suivant le nombre d'axes de symétrie présents ;
- suivant le type de symétrie présent.
En fait, tous ces classements sont équivalents.
Le triangle isocèle
 Pour les articles homonymes, voir Isocèle (homonymie).
Pour les articles homonymes, voir Isocèle (homonymie).Les trois propositions suivantes sont équivalentes :
- Un triangle a deux côtés de même longueur.
- Un triangle a deux angles de même mesure.
- Un triangle a un axe de symétrie.
Dans ce cas le triangle est dit isocèle. (On peut aussi dire isoangle). Isocèle du grec iso = même et scèle = jambe
Lorsqu'un triangle ABC est tel que AC = AB (les deux côtés d'extrémité A sont égaux), alors on dit que le triangle est isocèle de sommet A et que A est le sommet principal du triangle. Le côté [BC], opposé à A, est appelé base du triangle.
Lorsqu'un triangle est isocèle en A, la hauteur issue de A est aussi la médiatrice et la médiane du côté [BC] et la bissectrice de l'angle en A.
Un triangle bisocèle est un triangle isocèle qui, lorsqu'il est « coupé » en deux par la bissectrice d'un de ses angles, forme deux triangles isocèles eux aussi. Il n'y a que deux cas de triangles bisocèles : le triangle d'or et le triangle isocèle rectangle.
Lien externe : démonstration.Un triangle isocèle peut aussi se trouver dans la figure formée par un parallélogramme et ses diagonales : dans un rectangle, dans un losange ou dans un parallélogramme où la longueur d'un des côtés est la même que celle de la moitié d'une des diagonales.
Triangle équilatéral ou régulier
Article détaillé : Triangle équilatéral.Les propositions suivantes sont équivalentes :
- Un triangle a ses trois côtés de même longueur.
- Un triangle a ses trois angles de même mesure.
- Un triangle a trois axes de symétrie (bien que deux axes de symétrie suffisent).
Dans ce cas le triangle est dit équilatéral, ou équiangle, ou isopleure. Un triangle équilatéral peut être vu comme un triangle isocèle particulier.
Les trois angles d'un triangle équilatéral mesurent 60°. Par ailleurs, chacune des hauteurs issues d'un sommet est aussi la médiatrice et la médiane du côté opposé et la bissectrice de l'angle.
Le rapport entre la hauteur et le côté d'un triangle équilatéral est égal à (√3)/2, soit environ 0,866.
Le triangle équilatéral est celui qui présente la plus grande aire pour un périmètre donné. Ainsi, le triangle de plus grande aire et de périmètre égal à 3 est le triangle équilatéral de côté 1. Cette propriété est analysée dans l'article Isopérimétrie.
Triangle scalène ou irrégulier
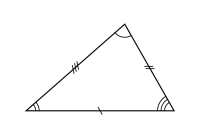 Triangle scalène
Triangle scalèneUn triangle scalène (du grec skalenos : boiteux, inégal, déséquilibré, oblique...) est un triangle :
- dont les trois côtés sont de longueurs différentes ;
- ou dont les trois angles sont de mesures différentes ;
- ou encore qui n'a pas d'axe de symétrie.
Les trois définitions ci-dessus sont équivalentes. Un tel triangle n'est bien sûr ni isocèle ni équilatéral, mais il peut être rectangle.
Triangle rectangle
Article détaillé : Triangle rectangle.Lorsqu'un triangle présente un angle droit (mesurant 90°) on parle de triangle rectangle.
Parmi les nombreuses propriétés du triangle rectangle, citons le fameux Théorème de Pythagore : « Un triangle admet un angle droit si et seulement si le carré de la longueur d'un de ses côtés est égal à la somme des carrés des longueurs des deux autres côtés. »
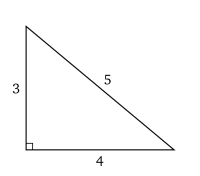 Triangle 3-4-5
Triangle 3-4-5Le 'triangle 3-4-5 est un triangle rectangle dont les longueurs des côtés forment une progression
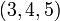 . On peut remarquer que 5² = 3² + 4² (soit 25 = 9 + 16) : comme ce triangle vérifie la relation du théorème de Pythagore on peut en déduire qu'il est rectangle.
. On peut remarquer que 5² = 3² + 4² (soit 25 = 9 + 16) : comme ce triangle vérifie la relation du théorème de Pythagore on peut en déduire qu'il est rectangle.Ce cas particulier d'un triangle rectangle est connu depuis l'Antiquité. Il est facile à réaliser à l'aide d'une corde à treize nœuds : on l'utilisait pour tracer un angle droit au sol. Pour cette raison, on l'appelle aussi « triangle des arpenteurs ».
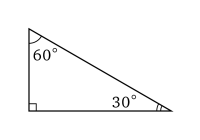 Triangle de l'écolier.
Triangle de l'écolier.Le triangle 30-60-90 est un triangle rectangle dont les angles mesurent 30°, 60° et 90°, c'est-à-dire forment une progression
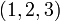 . Les longueurs des côtés forment quant à eux une progression
. Les longueurs des côtés forment quant à eux une progression 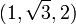 .
.Ce triangle est parfois aussi appelé « triangle de l'écolier » : les équerres d'écolier ont parfois cette forme. On parle aussi de « triangle hémi-équilatéral ». Cette dernière appellation se justifie en remarquant qu'un triangle équilatéral peut être coupé suivant un axe reliant l'un de ses sommets au milieu du côté opposé, pour donner deux triangles 30-60-90 égaux.
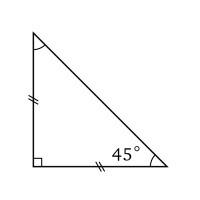 Triangle rectangle isocèle.
Triangle rectangle isocèle.Un triangle peut être à la fois rectangle et isocèle. Dans ce cas, il l'est au même sommet. Ses deux angles aigus mesurent 45° (ou π/4 rad).
C'est le triangle obtenu en divisant un carré en deux suivant une diagonale, d'où le nom du triangle : « demi-carré ».
Éléments remarquables du triangle
Remarque : les noms de hauteurs, médianes, médiatrices ou bissectrices désignent non seulement les droites indiquées ci-dessous, mais aussi les segments de ces droites intérieurs au triangle.
Médianes et centre de gravité
Article détaillé : Médiane (géométrie).On appelle médiane d'un triangle chacune des trois droites passant par un sommet du triangle et par le milieu du côté opposé à ce sommet.
Chacune des trois médianes divise le triangle en deux triangles d'aires égales.
Les trois médianes d'un triangle sont concourantes. Leur point d'intersection G est nommé centre de gravité du triangle. Si le triangle était une plaque solide homogène, on pourrait le faire tenir en équilibre sur une pointe en le posant exactement sur ce point G .
Le centre de gravité du triangle est aussi l'isobarycentre de ses sommets A, B et C, défini par la relation vectorielle :
-
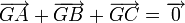 .
.
Si I désigne le milieu du côté [BC] on a la relation vectorielle :
-
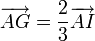 .
.
En effet, si I est l'isobarycentre de B et de C pondérés par des masses unité, alors par associativité G est le barycentre de I pondéré d'une masse 2 et de A pondéré d'une masse 1.
Cette relation s'applique également aux deux autres sommets du triangle vis-à-vis du milieu de leur côté opposé.
Si I , J et K désignent respectivement les milieux des côtés [BC] , [AC] et [AB], alors le triangle IJK est appelé triangle médian du triangle ABC .
Médiatrices et cercle circonscrit
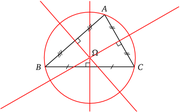
Article détaillé : Cercle circonscrit à un triangle.On appelle médiatrice d'un triangle chacune des médiatrices de ses côtés [AB], [AC] et [BC].
Les trois médiatrices d'un triangle sont concourantes en un point Ω équidistant des trois sommets. Le cercle de centre Ω et de rayon ΩA passe par chacun des trois sommets du triangle : c'est le cercle circonscrit au triangle. Tout triangle est donc un polygone inscriptible.
Remarques :
- Un triangle est obtusangle (ou ambligone) si et seulement si les médiatrices se coupent à l'extérieur du triangle
- Un triangle est acutangle (ou oxygone) si et seulement si les médiatrices se coupent à l'intérieur du triangle
Propriété :
- ABC est un triangle rectangle en A si et seulement si le centre de son cercle circonscrit est le milieu de [BC].
Bissectrices et cercle inscrit
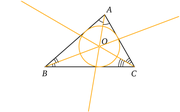
Article détaillé : Cercles inscrit et exinscrits d'un triangle.Les bissectrices d'un triangle sont les trois bissectrices intérieures de ses angles.
Les trois bissectrices d'un triangle sont concourantes en un point O. Le cercle inscrit au triangle est l'unique cercle tangent aux trois côtés du triangle et tout entier inclus dans le triangle. Il a pour centre le point O qui est donc le centre du cercle inscrit au triangle.
Hauteurs et orthocentre
Article détaillé : Hauteurs d'un triangle.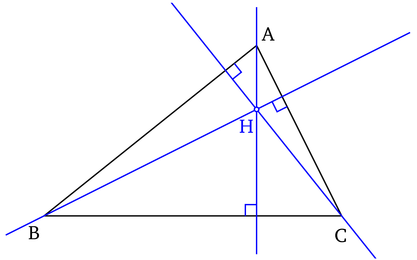 Hauteurs et orthocentre d'un triangle
Hauteurs et orthocentre d'un triangleOn appelle hauteur d'un triangle chacune des trois droites passant par un sommet du triangle et perpendiculaire au côté opposé à ce sommet. L'intersection de la hauteur et du côté opposé s'appelle « pied » de la hauteur. Ces 3 hauteurs se coupent en un point unique H appelé orthocentre du triangle.
Remarques :
- Un triangle est rectangle si et seulement si son orthocentre est un des sommets du triangle
- Un triangle est obtusangle (ou ambligone) si et seulement si son orthocentre est à l'extérieur du triangle
- Un triangle est acutangle (ou oxygone) si et seulement si son orthocentre est à l'intérieur du triangle
- Un triangle dont les sommets sont trois des quatre points A , B , C et H admet le quatrième de ces points comme orthocentre. On dit que les quatre points forment un groupe orthocentrique.
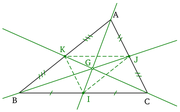
Droite et cercle d'Euler
Articles détaillés : Droite d'Euler et Cercle d'Euler.Les trois points H, G et Ω sont alignés sur une droite appelée droite d'Euler du triangle et vérifient la relation d'Euler :
Par ailleurs les milieux des trois côtés, les trois pieds des hauteurs et les milieux des segments [AH], [BH] et [CH] sont sur un même cercle dénommé cercle d'Euler ou cercle des neufs points du triangle.
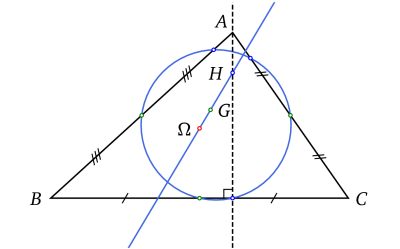 Droite et cercle d'Euler d'un triangle.
Droite et cercle d'Euler d'un triangle.Propriétés métriques du triangle
Aire d'un triangle
L'aire d'un triangle est l'aire de la portion du plan qu'il enferme. Il existe plusieurs manières de la calculer, selon les informations dont on veut partir.
Calcul à partir d'une hauteur
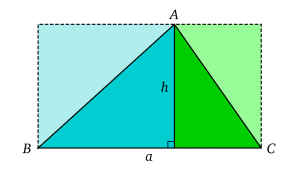 L'aire d'un triangle peut être calculée en le décomposant en deux triangles rectangles.
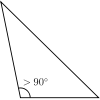
L'aire d'un triangle peut être calculée en le décomposant en deux triangles rectangles.Si le triangle est rectangle il est immédiat que son aire est
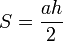 ,
,où a est la longueur d'un côté différent de l'hypoténuse et h la longueur de la hauteur issue de ce côté. Si le triangle n'est pas rectangle, la relation reste vraie, car le triangle se décompose en deux triangles rectangles (comme sur la figure).
À partir des longueurs des trois côtés
Pour une expression de l'aire d'un triangle dont les longueurs des côtés sont a, b et c et p le demi-périmètre [
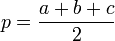 ], on peut utiliser la formule de Héron :
], on peut utiliser la formule de Héron :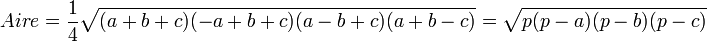 .
.À partir des coordonnées des sommets
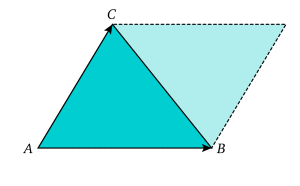 L'aire d'un triangle calculé à partir d'un parallélogramme.
L'aire d'un triangle calculé à partir d'un parallélogramme.L'aire du parallélogramme défini par deux vecteurs
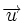 ,
, 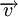 est la norme de leur produit vectoriel :
est la norme de leur produit vectoriel :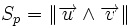 .
.On peut calculer l'aire d'un triangle à partir de cette formule :
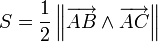 .
.Un repère orthonormé étant donné, l'aire du triangle ABC peut être calculée à partir des coordonnées des sommets.
Dans le plan, si les coordonnées de A, B et C sont données par A(xA,yA), B(xB,yB) et C(xC,yC), alors l'aire S est la moitié de la valeur absolue du déterminant
L'aire du triangle ABC peut aussi se calculer à partir de la formule
Cette méthode se généralise en trois dimensions. L'aire du triangle ABC où A = (xA,yA,zA), B = (xB,yB,zB) et C = (xC,yC,zC) s'exprime comme
Relations métriques dans un triangle
Article détaillé : Résolution d'un triangle.Notations :
- p désigne le demi-périmètre du triangle :
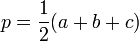 ;
; - S désigne l'aire de la surface du triangle ;
- R désigne le rayon du cercle circonscrit ;
- h désigne la hauteur relative au côté BC de longueur a ;
- r désigne le rayon du cercle inscrit ;
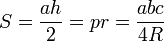 ;
;
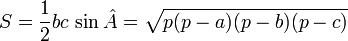 (Formule de Héron) ;
(Formule de Héron) ;
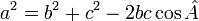 (Théorème d'Al-Kashi, ou Théorème de Pythagore généralisé) ;
(Théorème d'Al-Kashi, ou Théorème de Pythagore généralisé) ;
-
- Avec
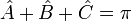 , les 2 dernières formules sont à la base des méthodes de triangulation en géodésie et astronomie.
, les 2 dernières formules sont à la base des méthodes de triangulation en géodésie et astronomie.
- Avec
Triangles isométriques, triangles semblables
On dit que deux triangles sont isométriques lorsqu'il existe une isométrie (c'est-à-dire une translation, une rotation, une symétrie ou une composée de telles transformations) qui transforme l'un en l'autre. Cela correspond à des triangles « superposables ». Pour qu'ils le soient, il suffit qu'une seule des conditions ci-dessous soit vérifiée :
- Leurs trois côtés ont même longueurs (abrégé par CCC) ;
- Deux côtés ont même longueurs, et l'angle compris entre ces deux côtés a même mesure (abrégé par CAC) ;
- Deux angles ont même mesures, et le côté commun à ces deux angles à même longueur (abrégé par ACA).
Deux triangles sont qualifiés de semblables lorsque leurs trois angles sont respectivement égaux un à un (abrégé par AAA). Il existe alors une similitude (qui est la composée d'une isométrie et d'une homothétie) qui transforme l'un en l'autre. Dans ce cas, les longueurs de leurs côtés sont proportionnelles.
Tous les triangles équilatéraux sont semblables.
Dans l'espace
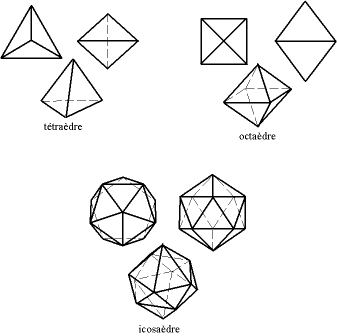
Polyèdres à faces triangulairesLe triangle est la forme des faces de nombreux polyèdres réguliers : tétraèdre (quatre faces qui sont des triangles équilatéraux, c'est la pyramide à base triangulaire), octaèdre (huit faces, les pyramides égyptiennes sont des demi-octaèdres), icosaèdre (vingt faces)...
Histoire
 Problèmes R49->R55 du papyrus Rhind
Problèmes R49->R55 du papyrus Rhind
Aucun document mathématique de l'Ancien Empire ne nous est parvenu. Mais l'architecture monumentale des IIIe et IVe dynastie constitue une preuve remarquable que les égyptiens de cette époque détenaient des connaissances relativement élaborées en géométrie, et en particulier dans l'étude des triangles.
Articles détaillés : Pyramide à faces lisses et Observation mathématique de la pyramide de Khéops.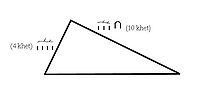 figure du triangle représentée dans le problème R51 du papyrus Rhind
figure du triangle représentée dans le problème R51 du papyrus Rhind
Le calcul de l'aire de cette figure est étudiée dans les problèmes R51 du papyrus Rhind, M4, M7 et M17 du papyrus de Moscou et datant tous du Moyen Empire. Le problème R51 constitue, dans l'histoire mondiale des mathématiques, le premier témoignage écrit traitant du calcul de l'aire d'un triangle.
- Énoncé du problème R51 du papyrus Rhind[1]
« Exemple de calcul d'un triangle de terre. Si quelqu'un te dit: Un triangle de 10 khet sur son mryt et de 4 khet sur sa base. Quelle est sa superficie ? Calcule la moitié de 4 qui est 2 pour en faire un rectangle. Tu fais en sorte de multiplier 10 par 2. Ceci est sa superficie. »Le terme mryt signifie probablement hauteur, ou côté. Mais la formule utilisée pour le calcul de l'aire fait pencher l'interprétation en faveur de la première solution[2]. Le scribe prenait la moitié de la base du triangle et calculait l'aire du rectangle formé par ce côté et la hauteur, soit
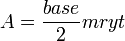
équivalente à la formule générale utilisée de nos jours :
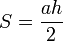
Le fait qu'un triangle de côtés 3-4-5 soit rectangle était également connu des anciens Égyptiens et Mésopotamiens.
Euclide, dans le livre I de ses Éléments, vers 300 av. J.-C, énonce la propriété sur la somme des angles du triangle et les trois cas d'égalité des triangles (voir ci-dessus le paragraphe sur les triangles isométriques).
Articles connexes
- Aire de surfaces usuelles
- Nombre triangulaire
- Liste des éléments remarquables d'un triangle
- Résolution d'un triangle
- Triangle de Pascal
- Triangle de Penrose
- Triangle de Sierpinski
- Triangle de Kobon
- Symbolique du triangle
Notes
- ↑ A. Buffum Chace, Rhind papyrus, pl. 73.
- ↑ C. Marshall, Ancient Egyptian Science, p.70
- Portail de la géométrie
Catégories : Mathématiques élémentaires | Géométrie du triangle | Polygone
Wikimedia Foundation. 2010.


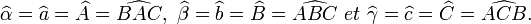
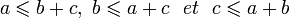


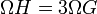
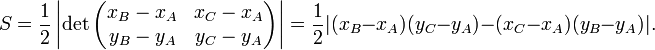
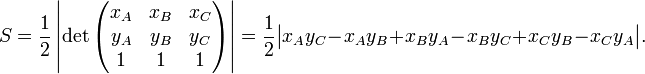
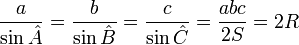 (
(