- Theoreme spectral
-
Théorème spectral
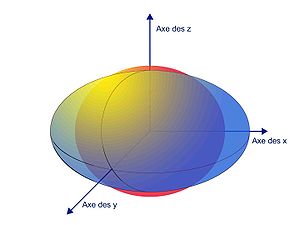
 Un ellipsoïde en trois possède autant d'axes de symétrie que l'espace de dimensions. Ils sont notés ici x, y et z.
Un ellipsoïde en trois possède autant d'axes de symétrie que l'espace de dimensions. Ils sont notés ici x, y et z.
En mathématiques, une quadrique désigne une surface d’un espace euclidien. Elle est définie par un polynôme du second degré dont les variables correspondent aux coordonnées d’un vecteur dans une base orthonormale. L’ellipsoïde ou l’hyperboloïde à une ou deux nappes en sont des exemples. Cette définition s’étend à toutes les dimensions finies et se généralisent aux nombres complexes. Une symétrie axiale est une transformation de l’espace. À chaque point est associé le point en vis-à-vis par rapport à un axe dit de symétrie. Le point de départ et d'arrivée définissent une droite perpendiculaire, sécante à cet axe et l’intersection correspond au milieu des points de départ et d'arrivée.
Les quadriques possèdent une propriété remarquable, il existe au moins autant d’axes de symétries que l’espace contient de dimensions. De plus, ces axes peuvent être choisis perpendiculaires entre eux. Il existe des cas pathologiques invalidant ce résultat, comme le paraboloïde elliptique. Ces quadriques, qualifiées de dégénérées par les mathématiciens, possèdent moins d’axes de symétries.
Ce même résultat s’exprime fort différemment selon le contexte utilisé. Il possède un équivalent en terme algébrique, linéaire ou bilinéaire et encore matriciel. Son champ d’application dépasse celui de l’algèbre et la géométrie. En mathématiques pures, il est utilisé pour résoudre des équations différentielles ou classifier les forme quadratiques, il est aussi appliqué au calcul numérique et aux statistiques. La physique en fait grand usage pour des questions de mécanique générale du solide ou du point.
Cette propriété apporte une réponse restée conjecturale plus d’un siècle, avant d’être démontrée par Karl Weierstrass (1815 - 1897) en 1858. Elle était nécessaire pour répondre à une question d’astronomie : la stabilité du système solaire. Si elle s’est avérée insuffisante pour une réponse complète, ce résultat eut néanmoins un brillant avenir. La généralisation à la dimension infinie ouvre une vaste théorie, dite spectrale. Elle est indispensable à la physique du XXe siècle, par exemple pour la mécanique quantique. Pour cette raison, ce résultat porte parfois le nom de théorème spectral.
Sommaire
Dimension algébrique de la propriété
Une quadrique est un objet structurant, un cas particulier essentiel est celui de la sphère, définir un tel objet dans un espace vectoriel revient à le munir d'une distance spécifique, dite euclidienne. Une méthode couramment utilisée consiste à utiliser une forme quadratique, c'est-à-dire une application de l'espace dans l'ensemble des réels positifs. La distance est définie comme la racine carrée de la forme quadratique du vecteur reliant les deux points. Utiliser la forme quadratique à la place de la distance est commode. Les racines carrées disparaissent, permettant une expression plus simple des formules. Ainsi, le théorème de Pythagore dans le plan s'écrit, si Φ est la forme quadratique associée à la distance et si θ1 et θ2 correspondent aux carrés des coordonnées dans une base orthonormale, par Φ = θ1 + θ2. Dans le cas d'une dimension finie quelconque : Φ = θ1 + θ2 + … + θn.
Une telle forme correspond à un cas particulier de quadrique. Elle est aussi définie par un polynôme de degré deux. Il est néanmoins homogène, c'est-à-dire qu'il ne contient que des termes de degré deux. Une quadrique homogène définit une deuxième forme quadratique Ψ et en conséquence une autre distance. Graphiquement, le contexte de la propriété de l'article est illustré par la figure de gauche. La distance d'origine est définie par la sphère rouge et celle de la quadrique associée à Ψ, par l'ellipsoïde bleu. Il existe alors une base qui respecte l'orthogonalité des deux formes quadratiques. Si l'orthogonalité est respectée, il n'en est pas de même pour les longueurs. Ainsi, le vecteur unitaire de l'axe des x pour la distance originale (en rouge) est de longueur plus petite pour la nouvelle distance (en bleu), d'où la nécessité d'un coefficient s1 pour passer d'une distance à l'autre.
 Seules les ellipsoïdes définissent une distance euclidienne. Un hyperboloïde définit une distance de nature différente, utilisée par exemple pour la relativité restreinte.
Seules les ellipsoïdes définissent une distance euclidienne. Un hyperboloïde définit une distance de nature différente, utilisée par exemple pour la relativité restreinte.
C'est en ces termes que Weierstrass exprime son théorème. Le vocabulaire évolue un peu avec le temps, le terme maintenant utilisé est celui de forme quadratique quand il parle de fonction homogène du second degré :
« Soit deux fonctions homogènes du second degré Φ, Ψ de n variables x1, x2, …. , alors il est en général possible, de les représenter de cette même forme
- Φ = θ1 + θ2 + … + θn
- Ψ = s1θ1 + s2θ2+…+snθn,
- θ1, θ2, …,θn étant des expressions quadratiques homogènes des x1,…xn et s1,… , sn des constantes. »[1]
Un tel formalisme généralise la notion de distance. Les valeurs de si n'ont aucune raison d'être toutes positives. Si tel n'est pas le cas, la sphère unité prend une apparence différente, analogue à un hyperboloïde. Une telle géométrie est utilisée en physique, dans le cadre de la relativité restreinte.
- Enfin, il existe un pont entre les formes quadratiques et les applications linéaires, construit à l'aide du produit scalaire. Il est ici noté < . , . >, c'est-à-dire que le produit scalaire de deux vecteurs u et v est noté < u , v >. A une application linéaire a de l'espace dans lui-même (appelé endomorphisme), est associé la forme quadratique Φa définie par Φa(u) = < a(u) , u >. Il existe de bons endomorphismes pour définir les formes quadratiques, ils sont nommés autoadjoints. Ils correspondent à ceux dont la matrice, dans une base orthonormée est symétrique, c'est-à-dire que les coefficients sont en miroir par rapport à la première diagonale. L'étude des endomorphismes autoadjoints est l'origine de la question traitée dans cet l'article.
Histoire
Origine mécanique
Article détaillé : mécanique du point. Jean le Rond d'Alembert trouve l'utilité dans une transformation, qui, plus tard, sera considérée comme la diagonalisation d'une matrice.
Jean le Rond d'Alembert trouve l'utilité dans une transformation, qui, plus tard, sera considérée comme la diagonalisation d'une matrice.
Plus d'un siècle avant la démonstration du théorème, apparaît ce qui, plus tard, sera considéré comme une matrice symétrique. Jean le Rond d'Alembert (1717 - 1783) cherche à connaitre le mouvement d'une corde vibrante[2]. Il modélise le phénomène par un élastique dont la masse est rassemblée en des points régulièrement espacés. Le problème mathématique correspond à une équation différentielle linéaire. Si les variations sont suffisamment petites, les coefficients associés sont constants. Leonhard Euler (1707 - 1783) propose une méthode dite des coefficients indéterminées pour expliciter la solution[3]. Contrairement aux prévisions de Daniel Bernoulli (1700 - 1782), une approche analytique permet de trouver une solution conforme à ses expériences : Je me contenterai de dire que l’on remarque aisément dans les valeurs de x & de y trouvées ci-dessus, la double oscillation que M. Bernouilli a observée dans le mouvement du pendule dont il s’agit[4]. Néanmoins, les prétentions à la généralité de d'Alembert s'avèrent inexactes. Les coefficients indéterminées permettent uniquement de résoudre les cas où seules deux ou trois masses sont présentes.
Pour traiter le cas d'un nombre de masses plus important, Joseph-Louis Lagrange (1736 - 1813) développe une nouvelle approche. Il utilise une pratique polynomiale spécifique s'affranchissant de la méthode des coefficients indéterminés[5]. Grâce au fait que les coefficients sont en miroir, ce qui, en terme moderne se traduit par le fait que l'endomorphisme est auto-adjoint, il utilise une astucieuse méthode sur les primes et les indices. Le polynôme trouvé correspond à ce qui est maintenant nommé le polynôme caractéristique.
La méthode utilisée est relativement générique. Elle correspond à une approximation linéaire tangente, à ce titre elle fait partie d'une vaste théorie dite des perturbations. Elle suppose aussi que l'endomorphisme associé est symétrique. Enfin, elle ne fonctionne que si les racines du polynôme caractéristique, maintenant appelé valeurs propres, sont toutes distinctes, enfin le cas des racines imaginaires fait peur. Les savants de l'époque en ont bien conscience : d’où l’on voit que le système est susceptible d’autant de différents mouvements isochrones que l’équation P=0 a de racines réelles négatives et inégales.[5]
Développement astronomique
 Joseph-Louis Lagrange étudie les perturbations des trajectoires des planètes engendrées par les autres masses que le soleil. La méthode proposée met en évidence des perturbations séculaires, phénomène qui s'avère être un moteur essentiel de la théorie pendant tout le XIXe siècle.
Joseph-Louis Lagrange étudie les perturbations des trajectoires des planètes engendrées par les autres masses que le soleil. La méthode proposée met en évidence des perturbations séculaires, phénomène qui s'avère être un moteur essentiel de la théorie pendant tout le XIXe siècle.
Une autre situation entre dans le domaine de validité de la méthode : celle de la trajectoire des planètes. En plus de l'attraction solaire, les planètes s'attirent entre elles et engendrent de petites perturbations. Lagrange les décrit de la manière suivante :
« Ces variations sont de deux espèces : les unes périodiques et qui ne dépendent que de la configuration des Planètes entre elles ; celles-ci sont les plus sensibles, et le calcul en a déjà été donné par différents Auteurs ; les autres séculaires et qui paraissent aller toujours en augmentant, ce sont les plus difficiles à déterminer tant par les observations que par la Théorie. ... Ces dernières altèrent les éléments mêmes de l’orbite, c'est-à-dire la position et la dimension de l’ellipse décrite par la planète ; et quoique leur effet soit insensible dans un court espace de temps, il peut néanmoins devenir à la longue très considérable. »[6]
Les variations séculaires fascinent, la stabilité du système solaire est menacée. Cet aspect s'avère un moteur théorique essentiel pour la compréhension du sujet de cet article. S'il existe une méthode numérique opérationnelle, elle ne peut garantir un résultat théorique tant que deux questions ne sont pas résolues. Que se passe-t-il s'il existe une valeur propre multiple ? Et sont elles toutes réelles ?
« ... il peut néanmoins arriver qu’il y en ait d’égales ou d’imaginaires ; mais il est facile de résoudre ces cas par les méthodes connues : nous observerons seulement que, dans le cas des racines égales, les valeurs de s, s1, s2,…, u, u1, u2,… contiendront des arcs de cercle, et que dans celui des racines imaginaires ces valeurs contiendront des exponentielles ordinaires ; de sorte que, dans l’un et l’autre cas, les quantités dont il s’agit croîtront à mesure que t croît ; par conséquent la solution précédente cessera d’être exacte au bout d’un certain temps ; mais heureusement ces cas ne paraissent pas avoir lieu dans le Système du monde. »[7]
La stabilité des perturbations du premier ordre, celles traitées par la méthode de Lagrange fait couler beaucoup d'encre. La réponse qu'il propose est celle du calcul effectif. Il suppose qu'une planète n'est en interaction qu'avec quatre autres et développe une méthode de substitution sur les polynômes pour en extraire les racines[8], qui s'avère soixante ans plus tard le point de départ de la théorie de Galois. Il en déduit :
« Cependant il ne parait pas impossible de parvenir, par quelque artifice particulier, à décider cette question d’une manière générale ; et comme c’est un objet également intéressant pour l’analyse et pour l’Astronomie physique, je me propose de m’en occuper. En attendant, je me contenterai de remarquer que, dans le cas présent, les racines trouvées sont trop différentes entre elles pour qu’un petit changement dans les masses adoptées puisse les rendre égales, et encore moins imaginaires »[6]
Pierre-Simon Laplace (1749 - 1827), ne se contente pas de la réponse numérique de Lagrange. Elle n'offre pas à son goût de garantie suffisamment solide de stabilité, que se passe-t-il avec la prise en compte de plus de planètes? Il démontre que la disposition en miroir des coefficients ainsi que la nature de leur valeur imposent une convergence si seul les effets du premier ordre sont pris en compte[9]. Sa méthode néanmoins ne possède aucun caractère générique et ne fait pas avancer les mathématiques. L'avenir montrera de plus que la convergence des perturbations d'ordre un ne garantit en rien la stabilité recherchée.
Géométrie analytique
Article détaillé : Géométrie analytique.Augustin Louis Cauchy donne une dimension géométrique au problème.
Quand, dans les années 1820, Augustin Louis Cauchy (1789 - 1857) s'attelle à cette question. Il n'est pas un novice en algèbre, son traité[10] sur les déterminants fait autorité. Son approche, si elle reste analytique, diffère radicalement de celle de Lagrange, qui se décrit ainsi :
« Les méthodes que j'y expose ne demandent ni constructions ni raisonnements géométriques ou mécaniques, mais seulement des opérations algébriques assujétties à une marche régulière et uniforme. »[11]
Cauchy découvre la dimension géométrique de la question. Il axe son analyse sur l'étude des quadriques. Elles sont définies de manière analytique par une forme quadratique, qu'il exprime comme un polynôme homogène du deuxième degré. Il remarque que, dans le cas de la dimension trois, il existe trois plans, définis par le choix de deux vecteurs pris parmi trois, qui divisent la quadrique en deux parties symétriques. Ces trois vecteurs sont orthogonaux et peuvent être choisis de longueur un. Pour trouver ces vecteurs, Cauchy analyse les extrema de la surface à l'aide des dérivées partielles. Il établit la correspondance entre ces axes et les vecteurs propres de l'application linéaire associé. Un calcul de déterminant, fondé sur les techniques qu'il a développées dans le passé lui permettent d'expliciter les valeurs propres[12], il correspond maintenant à ce qui est appelé le polynôme caractéristique, le même qu'avait trouvé, par des méthodes différentes, Lagrange.
Cauchy voit ainsi la question sous trois angles : trouver les valeurs propres et les vecteurs propres d'une application linéaire, étudier les formes quadratiques et classifier les quadriques. Il applique cette triple approche à trois situation : la classification de nombreuses surfaces du second degré dans un espace de dimension quelconque, l'étude des axes d'inertie d'un solide en rotation[13] et les variations séculaires[14]. Cauchy présente un mémoire[15].
Cette méthode possède deux faiblesses, toujours les mêmes. Si le polynôme caractéristique possède une racine multiple, alors il est impossible de déterminer les vecteurs propres et la nature réelle ou complexe des valeurs propres reste un inconnue. Dans le cas des axes d'inerties d'un solide, un artifice particulier, associé à son aspect tridimensionnel permet de résoudre la question, le cas général reste un mystère :
« D’après ce qui a été dit ci-dessus, il ne peut rester de doutes sur l’exactitude du théorème I, si ce n’est dans le cas où quelques valeurs de s vérifieraient à la fois les deux équations (36) S = 0, R = 0, Q = 0, … prises consécutivement. »[14]
La révolution de 1830, ainsi que la position politique de Cauchy (il est légitimiste) lui impose l'exil et l'arrêt de ses travaux. Une décennie plus tard, il revient sur ces questions pour mieux comprendre la propagation des ondes lumineuses ou d'origine élastique. Ces travaux donnent lieu à la création de l'expression polynôme caractéristique, ou plus précisément dans les textes de Cauchy d' équation caractéristique.[16]et[17]. Les travaux de Cauchy sur la stabilité du système solaire se traduisent in fine par un apport opposé à celui de Laplace : une importante avancée théorique associé à une absence de résultat concret.
Arithmétique et algèbre
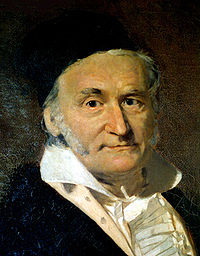 Avec l'arithmétique, Carl Friedrich Gauss introduit en Allemagne une approche purement algébrique pour l'étude des formes quadratiques.
Avec l'arithmétique, Carl Friedrich Gauss introduit en Allemagne une approche purement algébrique pour l'étude des formes quadratiques.
Le problème des variations séculaires peut aussi être mis en relation avec un vieux problème d'arithmétique soulevé par Pierre de Fermat (1601 - 1665) maintenant appelé théorème des deux carrés. La question posée est celle des nombres premiers s'exprimant sous la forme de deux carrés d'entiers. D'une manière plus générale cette question est reliée aux valeurs que peut prendre la forme quadratique x2 + y2 si x et y prennent des valeurs entières. Un regard encore plus général est celui des valeurs que peut prendre une forme quadratique quelconque sur les entiers. Il amène aux théorème des trois et des quatre carrés.
Un élément de réponse pour cette question correspond à la classification des formes quadratiques, en classes d'équivalences. Deux formes quadratiques Φ et Ψ sur un Z module M sont dites équivalentes s'il existe un endomorphisme bijectif f de M tel que Φ soit égal à la composée de Ψ et de f. Autrement dit si les formes quadratiques représentent le même objet dans deux bases différentes. Les formes ont la même image, il suffit donc de connaitre l'image d'une unique forme dans chaque classe pour résoudre une large famille d'équations diophantiennes. Cette classification arithmétique des formes quadratiques est initiée par Adrien-Marie Legendre[18] (1752 - 1833) en 1798 et rapidement poursuivi par Carl Friedrich Gauss[19] (1777 - 1855) en 1801. Cette démarche, éminemment linéaire, est à l'origine par Gauss de la première utilisation du terme déterminant.
La connaissance des formes quadratiques ne manquent pas d'avoir des applications. Un nouvel exemple est rapidement fourni, encore par l'astronomie. Les données associées à la trajectoire d'un corps céleste sont à la fois nombreuses et toutes entachées de petites erreurs. Utiliser la méthode des moindres carrés pour estimer précisément la trajectoire est fructueux et permet à Gauss de retrouver l'astéroïde Cérès (les détails sont données dans l'article sur la méthode des moindres carrés). Cette méthode consiste à trouver le minimum d'une forme quadratique, soit encore le vecteur propre de la plus petite valeur propre associée. Legendre est le premier à publier ce résultat, cependant Gauss ne lui reconnait pas la paternité de cette découverte. La réaction de Legendre est brutale : Cette impudence excessive est incroyable chez un homme au mérite personnel suffisant pour ne pas avoir besoin de s'approprier les découvertes d'autrui.[20]
 Charles Gustave Jacob Jacobi démontre que toute forme quadratique possède une base orthogonale.
Charles Gustave Jacob Jacobi démontre que toute forme quadratique possède une base orthogonale.
Dans le cas d'un espace vectoriel réel de dimension finie, la réduction d'une forme quadratique est réalisée par Charles Gustave Jacob Jacobi (1804 - 1851). Il montre qu'elles sont toutes équivalentes à une combinaison linéaire de carrés dont le coefficient est égal soit à 1 soit à -1[21]. Ce résultat est redécouvert par James Joseph Sylvester (1814 - 1897) et appliqué au principe de l'inertie des solides. Il porte maintenant son nom[22]. La distance entre le théorème de l'article et le savoir de l'époque devient ténue. Le résultat de Jacobi exprime que toute forme quadratique possède une base orthogonale. Il suffit d'en adjoindre une autre, définie positive pour conclure, ce que fait Weierstrass en 1858. Les techniques utilisées, comparables à celles des démonstrations données dans cet article, sont infiniment plus simples que celles de Cauchy.
Cette approche algébrique, dont l'Allemagne est probablement le plus riche contributeur avec Gauss, Jacobi, Ferdinand Eisenstein (1823 - 1852) ou Johann Peter Gustav Lejeune Dirichlet (1805 - 1859) est la solution, non seulement d'un problème d'algèbre, mais aussi des questions que se posent les français depuis longtemps. L'auteur en a parfaitement conscience :
« [Le problème] a été complètement résolu par Cauchy, Jacobi etc. pour le cas où l’on ne trouve aucune grandeur égale parmi s1, s2, ..., sn. Il n'est pas encore résolu en revanche dans les circonstances exceptionnelles où les racines de l’équation f(s)= 0 ne sont pas différentes l’une de l’autre, la difficulté qui se présente alors aurait déjà du être éclaircie et je propose de l'examiner attentivement plus en détail. Je ne pensais pas initialement qu'une solution serait possible sans des discussions spécifiques aux nombreux cas différents qui peuvent se produire. Il me fallait espérer que la résolution du problème soit susceptible d’une méthode indifférente à la multiplicité des grandeurs 1, s1, ..., sn. »[1]
Le théorème de Weierstrass éclaire la question des variations séculaires sous un autre angle, l'auteur du théorème conclut :
« Après avoir indiqué et énoncé la forme des intégrales, Lagrange a conclu que, comme les oscillations x1, dx1/dt restent toujours petites si elles le sont à l'origine, l’équation ne peut pas avoir de racines égales car les intégrales pourraient devenir arbitrairement grandes avec le temps. La même affirmation se trouve répétée chez Laplace lorsqu’il traite dans la Mécanique céleste des variations séculaires des planètes. Beaucoup d’autres auteurs, comme, par exemple, Poisson, mentionnent cette même conclusion. Mais cette conclusion n'est pas fondée […] et, si la fonction Ψ reste négative et de déterminant non nul, on peut énoncer le même résultat, que les racines de l’équation f(s)=0 soient ou non toutes distinctes ; l'homogénéité de cette conclusion n'a pu être découverte dans la passé car on a toujours envisagé ce cas [des racines multiples] par des approches particulières. »[1]
S'il est définitivement établi que les variations du premier ordre ne peuvent en aucun cas déstabiliser le système solaire, la question reste néanmoins ouverte : l'astronome Urbain Le Verrier (1811 - 1877) montre que les termes d'ordre deux ne peuvent être négligés. Il faut attendre le siècle suivant et le talent de Henri Poincaré (1854 - 1912) pour conclure positivement.[23]
Formalisation algébrique
 Karl Weierstrass propose la formulation algébrique de la propriété des quadriques, souvent connu sous le nom de théorème spectral.
Karl Weierstrass propose la formulation algébrique de la propriété des quadriques, souvent connu sous le nom de théorème spectral.
L'approche rigoureuse de la propriété de l'article se formalise mieux dans un contexte algébrique. C'est tout d'abord celui qui finit par prévaloir historiquement. Les démonstrations de Cauchy sont plus longues et surtout moins exhaustives (même s'il est possible de retrouver l'intégralité des propriétés). Les énoncées sont plus concis et enfin, la formalisation algébrique s'adapte mieux aux multiples applications dans des domaines si diverses.
Un formalisme contemporain modifie peu l'expression du théorème de Weierstrass, qui prend le nom de théorème spectral. Ce théorème possède de nombreuses généralisations en dimension infinie sans pour autant voir son nom modifié. Cette formulation possède un corollaire immédiat : la loi d'inertie de Sylvester stipulant que toute forme Ψ quadratique ou hermitienne possède une base orthogonale B tel que l'image de tout élément de B par Ψ est égale à 1 ou -1.
Théorème spectral en dimension finie — Soit E un espace vectoriel de dimension finie sur le corps des réels (resp. des complexes) et Φ, Ψ deux formes bilinéaires symétriques (resp. sesquilinéaire) de E tel que Φ soit définie positive. Alors il existe une base B de E orthonormale pour Φ et orthogonale pour Ψ. Dans cette base, les coefficients de la matrice associée à Ψ sont tous réels.
Ce résultat possède un équivalent en terme d'algèbre linéaire. Il entre dans la famille des outils visant à la réduction de l'endomorphisme. Il traite le cas particulier où l'application linéaire possède une structure compatible avec le produit scalaire :
Formalisme fondé sur un endomorphisme — Soit E un espace vectoriel euclidien (resp. hermitien), tout endomorphisme auto-adjoint est diagonalisable dans une base orthonormale et ses valeurs propres sont toutes réelles.
Sous cette forme, le théorème se généralise. L'analyse de la démonstration montre qu'il n'est pas nécessaire que l'endomorphisme soit auto-adjoint, il suffit qu'il soit normal, c'est-à-dire qu'il commute avec son adjoint. En revanche et sous cette forme, il ne s'applique plus au cas réel. Une rotation réelle dans un espace de dimension deux n'est en général pas diagonalisable, même si l'endomorphisme est normal.
Généralisation — Soit E un espace vectoriel hermitien, tout endomorphisme normal est diagonalisable dans une base orthonormale.
Tout théorème sur un endomorphisme possède son équivalent en termes de matrice car les deux structures sont isomorphes. Le théorème suivant est une transcription en termes matriciels. Les deux autres formes du théorème possèdent un équivalent tout aussi immédiat.
Formalisme matriciel — Soit A une matrice symétrique (resp. hermitienne), alors il existe une matrice P orthogonale (resp. unitaire) et une matrice D diagonale dont tous les coefficients sont réels, telles que la matrice A est égale à P.D.P-1 .
Démonstrations-
- Soit E un espace vectoriel hermitien, tout endomorphisme normal u est diagonalisable dans une base orthonormale.
Raisonnons par récurrence sur la dimension n de E.
Si n est égal à 1, alors l'application u est une homothétie et le résultat est démontré.
Supposons la propriété démontrée pour tout entier inférieur ou égal à p et supposons que n soit égal à p + 1. Le polynôme caractéristique de u est scindé car le corps des complexes est algébriquement clos. Soit λ une valeur propre et V l'espace propre associé à λ. Notons < . , . > le produit scalaire de E et F l'orthogonal de V. Montrons que V est stable par u* l'adjoint de u :
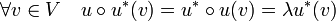
Les égalités précédentes montrent que u*(v) est bien un élément de V. Cette propriété implique F est stable par u, c'est à dire que u(F) est bien orthogonal à V, en effet :
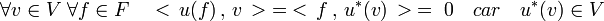
Sur V, u est diagonalisable dans une base orthonormale car la restriction de u à V est une homothétie. Sur F la restriction de u est aussi diagonalisable dans une base orthonormale par hypothèse de récurrence. E est somme directe orthogonale de V et F, ce qui termine la démonstration.
-
- Soit E un espace vectoriel hermitien ou euclidien, tout endomorphisme auto-adjoint u n'admet que des valeurs propres réelles.
Si E est hermitien, soit λ une valeur propre (qui existe toujours car le corps est algébriquement clos) et v un vecteur propre associé à la valeur λ. Comme v n'est pas nul, son produit scalaire ne l'est pas non plus. Les égalités suivantes montrent que λ est réel :
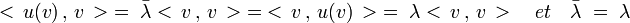
Si E est euclidien, le polynôme caractéristique de v est aussi le polynôme caractéristique d'un endomorphisme auto-adjoint : celui de même matrice dans un espace hermitien, le polynôme est donc scindé dans R, l'ensemble des réels.
La proposition précédente permet de conclure que tout endomorphisme auto-ajdoint est diagonalisable dans une base orthonormée avec des valeurs propres uniquement réelles.
-
- Soit E un espace euclidien (resp. hermitien) et Φ, Ψ deux formes quadratiques (resp. hermitienne) de E tel que Φ soit définie positive. Alors il existe une base B de E orthonormale pour Φ et orthogonale pour Ψ. Dans cette base, les coefficients de la matrice associée à Ψ sont tous réels.
Notons < . , . > le produit scalaire associé à Φ et u l'endomorphisme auto-adjoint tel que si v est élément de E, alors Ψ(u) = < u(v) , v >. Un tel endomorphisme existe, et est unique. La base orthonormale qui diagonalise u est celle qui répond à la proposition.
L'isomorphisme entre l'espace des endomorphismes et celui des matrices démontrent les propriétés équivalentes pour les matrices.
Pour une autre preuve dans le cas euclidien, voir l'article Orthogonalisation simultanée
Classification des quadriques
Cas d'une quadrique homogène
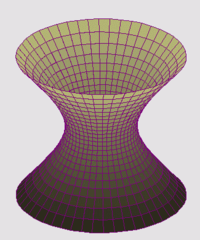
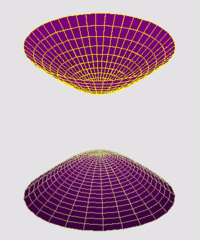 Certains axes de symétrie de l'hyperboloïde à deux nappes ne croisent pas la quadrique. Tel est le cas pour les axes horizontaux.
Certains axes de symétrie de l'hyperboloïde à deux nappes ne croisent pas la quadrique. Tel est le cas pour les axes horizontaux.
Si l'approche algébrique est la plus générale et la plus concise, la géométrie permet néanmoins d'établir certains résultats. Cette voie fût celle de Cauchy. L'article utilise la formalisation moderne issue de la géométrie différentielle, relativement différente de celle analytique du XIXe siècle.
Soit E un espace vectoriel euclidien de dimension n (ei) une base orthonormale B de E et S une surface quadrique définie par une forme quadratique Ψ. L'objectif est d'étudier les extrema de Ψ sur la variété différentielle qu'est la sphère de rayon l'unité. Ici le terme d'extremum de la quadrique désigne un point de cette nature, elle permet de trouver des axes de symétries même si un tel axe ne croisent pas la surface, comme dans le cas de l'hyperboloïde à deux nappes.
Axe de symétrie et vecteur propre — Un vecteur u de la sphère unité correspond à un extremum local pour la forme Ψ si et seulement s'il est vecteur propre de l'endomorphisme autoadjoint a associé à la forme Ψ. Un tel vecteur est la direction d'un axe de symétrie de la quadrique.
En effet, la fonction Ψ ainsi que la sphère en tant que variété différentielle sont de classe C∞, les extrema se caractérisent donc par des annulations de différentielles. Plus précisément, u est un extremum local si et seulement si le noyau de Ψ est inclus dans l'espace tangent à la sphère au point u.
La sphère est l'image réciproque de {1} par l'application qui à un vecteur v associe < v , v >. La différentielle de cette application en v est la forme linéaire qui au vecteur h associe 2<v , h >. Son noyau est donc l'hyperplan orthogonal de v. Soit a l'endomorphisme autoadjoint associé à la quadrique, Ψ est alors l'application qui à un vecteur v associe < a(v) , v >. Sa différentielle en u est l'application qui, à un vecteur h, associe le scalaire DΨu(h) égal à 2< a(u) , h >.
Comme u est un vecteur extremum, DΨu est nul sur l'hyperplan orthogonal de u, le vecteur a(u) est donc orthogonal à l'orthogonal de u, ce qui signifie qu'il est colinéaire à u. C'est bien la définition d'un vecteur propre.
Réciproquement, si u est un vecteur propre, alors le théorème précédent sur les endomorphismes autoadjoints montre que l'orthogonal de u est stable par a et donc que le noyau de DΨu est bien l'orthogonal de u, ce qui montre que le vecteur est un extremum.
Montrons enfin que u définit un axe de symétrie de la quadrique. Soit v un vecteur quelconque de la quadrique. v est somme d'un vecteur colinéaire à u et d'un vecteur w orthogonal : v = α.u + h. Si λ est la valeur propre de u, alors l'image ω de w par la symétrie axiale de direction u est ω = α.u - h. Il suffit alors de montrer que Ψ(ω) est égal à Ψ(v). Cette propriété est une conséquence directe du fait que u est orthogonal à h :
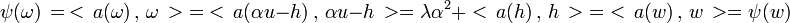
Les résultats algébriques précédents permettent de conclure :
Existence de n axes de symétries — Toute quadrique homogène possèdent n axes de symétries orthogonaux deux à deux.
En effet, il existe une base orthogonale de vecteurs propres de a.
Cas d'une quadrique non dégénérée
Si le cas réellement intéressant est celui que la quadrique homogène, à cause de sa dimension algébrique. Il n'est pas inutile que classifier les quadriques. Dans le cas général, une quadrique comporte aussi des termes d'ordre un, le polynôme est alors la somme d'une forme quadratique, d'une forme linéaire et d'une constante. En utilisant les notations précédentes il existe alors un vecteur b tel que la quadrique possède pour image d'un vecteur v quelconque < a(v) , v > + < b , v > - c. Si l'application a est un automorphisme, c'est à dire s'il est bijectif, alors la forme quadratique associée ainsi que la quadrique sont qualifiées de non dégénérée. Un simple changement de l'origine permet de se ramener à la situation précédente.
Supposons a bijectif, alors 1/2.b admet un antécédent β par a. Le polynôme P prend la forme suivante :
![\forall v \in E \quad P[v] \, = \, <a(v) \, , \, v> \, + \, 2<a(\beta) \, , \, v> \, + \, <a(\beta) \, , \, a(\beta)> \, - \, <a(\beta) \, , \, a(\beta)> - c](/pictures/frwiki/48/00b941f354310afc99cc998fc5c1da42.png)
On en déduit l'égalité :
![\forall v \in E \quad P[v] \, = \, <a(v + \beta) \, , \, v + \beta> - \; c_1 \quad avec \quad c_1 \,= \, c \ + \,, <a(\beta) \, , \, a(\beta)>](/pictures/frwiki/52/4450eb03e6636938829354cc63b03fe7.png)
La situation est donc géométriquement analogue à la précédente.
Cas général
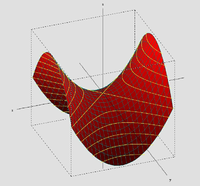 Même dans le cas dégénéré, les axes principaux sont parfois aussi des axes de symétries, comme c'est le cas pour le paraboloïde hyperbolique.
Même dans le cas dégénéré, les axes principaux sont parfois aussi des axes de symétries, comme c'est le cas pour le paraboloïde hyperbolique.
L'analyse précédente permet d'établir une rapide classification des quadriques. Le cas général est entièrement traité si le vecteur b est dans l'image de l'endomorphisme a. Il correspond à une équation de la forme :
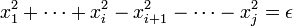
ε désigne ici un entier égal à zéro ou à un. La base dans laquelle les coordonnées s'expriment est orthogonale mais n'est plus normée, la norme des vecteurs est choisie pour égaler à un ou son inverse les coefficients de la quadrique. La quadrique est non dégénérée si et seulement si j est égal à n.
Dans le cas ou la quadrique est dégénérée et ou b n'est pas dans le noyau de l'endomorphisme a. Il est alors possible de choisir comme dernier vecteur de la base un élément de la droite de direction b. Et, quitte à translater l'origine, il existe encore une base orthogonale tel que l'équation de la quadrique prenne la forme suivante :
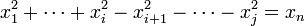
Dans ce cas j est toujours strictement plus petit que n, les vecteurs propres de la forme quadratique ne sont plus toujours des axes de symétrie comme le montre le paraboloïde de l'introduction. Pour cette raison, et pour obtenir un vocabulaire parfaitement générique, on appelle axe principal toute droite passant par l'origine (une fois la translation réalisée) et de direction une droite de vecteurs propres.
Applications
Pendule de D'Alembert à deux boules
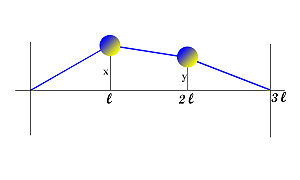 La corde vibrante est ici modélisée par un pendule dont la masse est concentrée en deux points régulièrement espacés.
La corde vibrante est ici modélisée par un pendule dont la masse est concentrée en deux points régulièrement espacés.
D'Alembert, dans la deuxième édition de son traité de dynamique, propose de résoudre l'équation du pendule illustré sur la figure de droite. La corde est élastique et de masse nulle, les deux parois sur lesquelles elle est maintenue est fixe. Enfin, les oscillations des deux masses, dont les coordonnées verticales sont notées x et y, sont petites devant l. Les deux boules sont régulièrement espacées et de même masse. Dans ce contexte la première masse reçoit une force vertical, proportionnelle à -2x + y et la deuxième à -2y + x.
Si E est l'espace vectoriel des couples (x, y), f la fonction du temps à valeur dans E décrivant la trajectoire du pendule, a l'endomorphisme défini par la matrice suivante, il existe une constante k tel que :
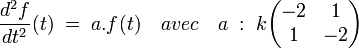
L'endomorphisme a dispose d'une matrice réelle symétrique, il est donc autoadjoint. L'existence d'une base orthonormée diagonalisant a permet de séparer les variables et donc de résoudre l'équation différentielle. D'Alembert, qui ne dispose pas de ce formalisme, utilise le théorème grâce à la méthode d'Euler dite des coefficients indéterminés. Elle se fonde sur l'utilisation du changement de variable suivant, si λ est un réel :
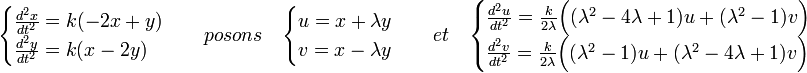
Choisir pour valeur de λ un permet de séparer les variables, le système devient :
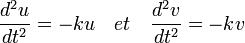
En terme moderne, u et v correspondent à deux vecteurs propres de a formant une base orthonormale dont les coordonnées dans la base canonique est 2/√2 (1, 1) et 2/√2 (-1, 1).
Pendule de D'Alembert à trois boules
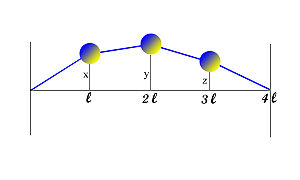 La corde vibrante est ici modélisée par un pendule dont la masse est concentrée en trois points régulièrement espacés.
La corde vibrante est ici modélisée par un pendule dont la masse est concentrée en trois points régulièrement espacés.
Les hypothèses et notations sont équivalentes à celles du paragraphe précédent, l'espace vectoriel E est maintenant celui des triplets (x, y, z).
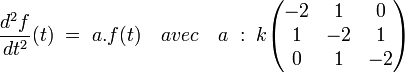
Il existe une base de vecteurs propres orthonormaux, d'après le théorème de l'article. Le calcul du polynôme caractéristique P[X] donne les valeurs propres λ1, λ2 et λ3 :
![P[X] = k^3(X+2)(X^2 + 4X +2) \quad donc \quad \lambda_1 = -2 \, , \, \lambda_2 = -2 + \sqrt 2 \; et \; \lambda_3 = -2 - \sqrt 2](/pictures/frwiki/48/0ac181828bdcb682eba64e5b29851ce6.png)
On en déduit les trois vecteurs propres associées v1, v2 et v3:
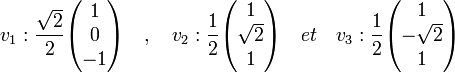
Généralisations
Réciproque
Si un endomorphisme est diagonalisable dans une base orthonormée et que les valeurs propres sont toutes réelles, alors il est clairement auto-adjoint.
En revanche, un endomorphisme est parfois diagonalisable sans être normal. Il suffit, par exemple de considérer un endomorphisme dont les racines du polynôme caractéristique sont toutes distinctes et dont les vecteurs propres ne forment pas une base orthogonale.
Généralisation en dimension finie
Articles détaillés : Diagonalisation et Réduction d'endomorphisme.Il est possible d'étudier la possible diagonalisation d'un endomorphisme sans produit scalaire. Une condition nécessaire et suffisante est donnée par le polynôme minimal. Un endomorphisme sur un espace vectoriel de dimension finie est diagonalisable si et seulement si le polynôme minimal est scindé et ne contient aucune racine multiple.
Le cas général est traité par Jordan (1838-1922) si le polynôme minimal est scindé[24]. L'endomorphisme n'est pas toujours diagonalisable, en revanche une forme canonique existe dans le cas général, permettant ainsi une réduction de l'endomorphisme.
La dimension infinie
Articles détaillés : Opérateur compact et Théorie de Sturm-Liouville.La tentation de généraliser le théorème à la dimension infinie est grande. L'exemple historique de la théorie est celui d'une corde vibrante, une modélisation exacte suppose une infinité de masses et impose donc un espace de dimension infinie. D'autres équations aux dérivées partielles se modélisent par un passage à la dimension infinie. Celle de la propagation de la chaleur est un exemple.
Notes et références
Articles connexes
- Réduction d'endomorphisme, diagonalisation, trigonalisation, Orthogonalisation simultanée ;
- Décomposition en valeurs singulières ;
Articles de mathématiques en rapport avec l'algèbre bilinéaireEspace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz
Notes
- ↑ a , b et c Karl Weierstrass Uber ein die homogenen Functionen zweiten Grades betreffendes Theorem M’ber. Akad. der Wiss. Berlin 1858 traduction Frédéric Brechenmacher
- ↑ Jean le Rond d'Alembert Traité de dynamique Paris 1743
- ↑ Leonhard Euler Recherches sur la connaissance mécanique des corps Mémoire de l’académie des sciences de Berlin 1758 ou Opera omnia Vol 2 pp 178 199 Zurich 1964
- ↑ Jean le Rond d'Alembert Traité de dynamique 2de ed. Paris 1758 page 152
- ↑ a et b Joseph-Louis Lagrange Solutions de différents problèmes de calcul intégral..., 1766 disponible dans Miscellanea Taurinensia Lagrange 1867-92 vol.1 pp 471-668
- ↑ a et b Joseph-Louis Lagrange Théorie des variations séculaires des éléments des planètes Nouv. mém. de l’acad. des sciences de Berlin Vol 1 p 125 1783
- ↑ Joseph-Louis Lagrange Recherches sur les équations séculaires des mouvements des noeuds, et des inclinaisons des orbites des planètes Hist. de l’acad. des sciences 1778
- ↑ Joseph-Louis Lagrange Réflexions sur la résolution algébrique des équations Mémoires de l'Académie royale des sciences et belles-lettres de Berlin 1770
- ↑ Pierre-Simon Laplace Mémoire sur les variations séculaires des orbites des planètes Mem. de l’acad. des sciences de Paris Oeuvres 11 pp 295-306 publié en 1795 soumis en 1789 lire sur Gallica page 88 à 92
- ↑ Cauchy Mémoire sur les fonctions qui ne peuvent obtenir que deux valeurs égales et des signes contraires par suite des transpositions opérées entre les variables qu'elles renferment adressé en 1812 et publié dans le Journal de l'Ecole Poytechnique, XVIIe Cahier, Tome X, Paris 1815 lire sur Gallica
- ↑ Joseph-Louis Lagrange Méchanique analytique Paris. 2de ed. Paris 1811
- ↑ Augustin Louis Cauchy Sur les centres, les plans principaux et les axes principaux des surfaces du second degré Exer. de math.3 = Œuvres (2)8, pp 8 35 1828
- ↑ Augustin Louis Cauchy Mémoire sur l’équation qui a pour racines les moments d’inertie principaux d’un corps solide et sur diverses équations du même genre Mémoires de l'Académie des sciences, t. IX, p. 111; présenté en 1826 et publié en 1830
- ↑ a et b Augustin Louis Cauchy Sur l’équation à l’aide de laquelle on détermine les inégalités séculaires du mouvement des planètes Exer. de math. 4 = Œuvres (2)9, pp 174 195 1829
- ↑ Augustin Louis Cauchy L’équation qui a pour racines les moments d’inertie principaux d’un corps solide, et sur diverses équations du même genre Mem. Acad. des Sci. Paris 1830
- ↑ Augustin Louis Cauchy Méthode générale propre à fournir les équations de condition relatives aux limites des corps dans les problèmes de physique mathématique Comptes rendus Acad. Sci. 8 Paris pp 79-81 1940 lu en 1939
- ↑ Augustin Louis Cauchy Mémoire sur l’intégration des équations linéaires Comptes rendus Acad. Sci. 30 Paris pp 202-211 1940 lu en 1939
- ↑ Adrien-Marie Legendre Théorie des nombres, Paris Duprat 1798
- ↑ Carl Friedrich Gauss Disquisitiones arithmeticae 1801
- ↑ S M Stigler Une Attaque de Gauss publié par Legendre en 1820 Historia Math. Vol 4 pp 31-35 1977
- ↑ Charles Gustave Jacob Jacobi Sur la réduction des formes quadratiques au plus petit nombre de termes Comptes rendus de l'Académie des sciences de Berlin 1848
- ↑ James Joseph Sylvester Théorie sur les invariants algébriques 1852
- ↑ La conséquence des perturbations d'ordre deux est étudiée par Le Verrier en 1856, voir par exemple Jacques Laskar La stabilité du système solaire Seuil pp 184-187 1992 (ISBN 2-02-015182-0) Lire
- ↑ Marie Ennemond Camille Jordan Traité des substitutions et des équations algébriques 1870
Liens externes
- (en) Abstract linear spaces Par l'Université de St Andrew
- (fr) L'identité algébrique d'une pratique portée par la discussion sur l'équation à l'aide de laquelle on détermine les inégalités séculaires des planètes par Frédéric Brechenmacher comporte une grande partie de l'analyse sous-jacente à la partie historique, il est aussi l'auteur des traductions des différentes citations de Weierstrass.
Références
- N. et J. Dhombres Naissance d’un pouvoir : sciences et savants en France 1793 - 1824 Payot 1989 (ISBN 2228881074)
Un livre qui retrace le contexte scientifique de l'époque, particulièrement l'importance de l'approche analytique en France p 470
- Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808)[détail des éditions]
Une référence sur l'algèbre, il traite intégralement les démonstrations algébriques de l'article- Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
Une introduction à l'analyse fonctionnelle, il traite des opérateurs autoadjoints compact et introduit l'opérateur de Fredholm- Portail des mathématiques
Catégories : Algèbre bilinéaire | Théorème de mathématiques
Wikimedia Foundation. 2010.