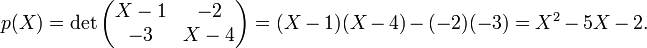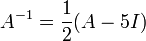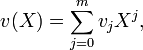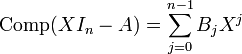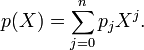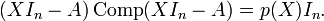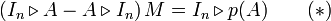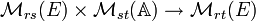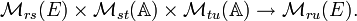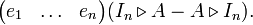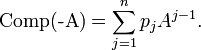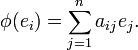Theoreme de Cayley-Hamilton

Théorème de Cayley-Hamilton

Pour les articles homonymes, voir Hamilton.

En algèbre linéaire, le théorème de Cayley-Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d'un espace vectoriel de dimension finie sur un corps quelconque annule son propre polynôme caractéristique.

En termes de matrice, cela signifie que :

si A est une matrice carrée d'ordre n et si

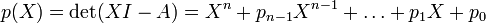
$p(X)= \det(XI-A) = X^n + p_{n-1}X^{n-1} + \ldots + p_1 X + p_0$

est son polynôme caractéristique (polynôme d'indéterminée X), alors en remplaçant formellement X par la matrice A dans le polynôme, le résultat est la matrice nulle :

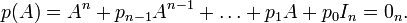
$p(A)= A^n + p_{n-1}A^{n-1} + \ldots + p_1 A + p_0 I_n = 0_n.\;$

Le théorème de Cayley-Hamilton s'applique aussi à des matrices carrées à coefficients dans un anneau commutatif quelconque.

Un corollaire important du théorème de Cayley-Hamilton affirme que le polynôme minimal d'une matrice donnée est un diviseur de son polynôme caractéristique.

Motivation

Ce théorème possède deux familles d'utilisation:

Il permet d'établir des résultats théoriques, par exemple pour calculer le polynôme caractéristique d'un endomorphisme nilpotent.
Il autorise aussi des simplifications puissantes dans les calculs de matrices. L'approche par les polynômes minimaux est en général moins coûteuse que celle par les déterminants.

On trouve ce théorème utilisé dans les articles sur les polynômes d'endomorphisme, endomorphismes nilpotents, et plus généralement dans la théorie générale des matrices

Exemple

Considérons par exemple la matrice

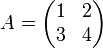$A = \begin{pmatrix}1&2\\ 3&4\end{pmatrix}$ .

Le polynôme caractéristique s'écrit

$p(X)=\det\begin{pmatrix}X-1&-2\\ -3&X-4\end{pmatrix}=(X-1)(X-4)-(-2)(-3)=X^2-5X-2.$

Le théorème de Cayley-Hamilton affirme que

A 2 - 5 A - 2 I 2 = 0

et cette relation peut être rapidement vérifiée dans ce cas. De plus le théorème de Cayley-Hamilton permet de calculer les puissances d'une matrice plus simplement que par un calcul direct. Reprenons la relation précédente

A 2 - 5 A - 2 I 2 = 0

A 2 = 5 A + 2 I 2

Ainsi, par exemple, pour calculer A⁴, nous pouvons écrire

A 3 = (5 A + 2 I 2) A = 5 A 2 + 2 A = 5(5 A + 2 I 2) + 2 A = 27 A + 10 I 2

et il vient

A 4 = A 3 A = (27 A + 10 I 2) A = 27 A 2 + 10 A = 27(5 A + 2 I 2) + 10 A

A 4 = 145 A + 54 I 2

On peut également utiliser la relation polynomiale initiale $A 2 - 5 A - 2 I 2 = 0$ pour prouver l'inversibilité de A et calculer son inverse. Il suffit en effet de mettre en facteur une puissance de A là où c'est possible et

A (A - 5 I) = 2 I 2

ce qui montre que A admet pour inverse

$A^{-1} = \frac12 (A-5I)$

Démonstration

Raisonnements faux

La plus grande difficulté de la démonstration du théorème de Cayley-Hamilton est qu'on peut se laisser piéger facilement par des raisonnements faux, et il importe de comprendre en quoi ces raisonnements sont faux, avant de tenter une démonstration correcte.

Dans la plupart des cas, ces erreurs proviennent de ce qu'on a appliqué un raisonnement valide dans un contexte commutatif au cas des matrices, dont l'arithmétique n'est pas commutative.

Un raisonnement naïvement faux

Le plus simple de tous les raisonnements faux est encore plus grossier : le polynôme caractéristique est défini par $p (X) = det(X I n - A)$ ; si on substitue $A$ à $X$ , on devrait avoir $p (A) = 0$ , ce qui n'a guère de sens. En effet, $X I n$ est une matrice diagonale 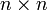$n\times n$ , avec des $X$ sur la diagonale. On peut imaginer une matrice diagonale par blocs, dont la diagonale serait formée de $n$ blocs égaux à $A$ . Bien sûr, cette matrice n'a pas la bonne taille pour qu'on puisse fabriquer sa différence avec $A$ . On peut aussi imaginer de remplacer $X I n$ par $A I n = A$ , mais dans ce cas, le résultat $det(A - A)$ est un scalaire nul, alors qu'on attendrait une matrice 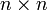$n\times n$ nulle.

Il convient de remarquer que l'énoncé du théorème pourrait être troublant, puisqu'on prend un polynôme 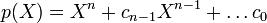$p(X)=X^n+c_{n-1}X^{n-1}+\dots c_0$ à coefficients scalaires, et qu'on substitue $A$ à l'indéterminée $X$ . Cette opération est définie sans ambiguïté : elle revient à remplacer $X j$ par $A j$ pour 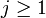$j\ge 1$ ; de plus, elle remplace le terme constant $c 0$ par $c 0 I n$ et elle évalue la combinaison linéaire de matrices 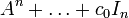$A^n+\dots+c_0I_n$ dans l'espace vectoriel 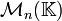$\mathcal{M}_n(\mathbb{K})$ des matrices carrées à coefficients dans $\mathbb{K}$ . 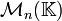Dans un langage plus abstrait, on peut dire qu'il existe un unique homomorphisme d'anneau de $\mathbb{K}[X]$ dans $\mathcal{M}_n(\mathbb{K})$ , qui envoie $X$ sur $A$ , et que $p (A)$ est l'image de $A$ par cet homomorphisme, dit homomorphisme d'évaluation.

Une idée correcte, mais qui finit mal

Un raisonnement plus compliqué, mais toujours faux, commence par le fait suivant, qui est d'ailleurs un ingrédient essentiel d'une preuve correcte : quelle que soit la matrice 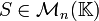$S \in \mathcal{M}_n(\mathbb{K})$ , il existe une matrice explicitement déterminée, $Comp(S)$ , la matrice complémentaire de S, qui vérifie $S Comp(S) = Comp(S) S = det S I n$ . La matrice $Comp(S)$ est la transposée de la comatrice ou matrice des cofacteurs de $S$ . Cette relation reste encore vraie si les coefficients de $S$ appartiennent à un anneau, puisqu'on n'a pas fait de divisions. On peut donc poser $S = X I n - A$ , dont les coefficients sont dans $\mathbb{K}[X]$ et on a alors la relation:

(X I n - A)Comp(X I n - A) = det(X I n - A) I n = p (X) I n .

(1)

Une fois parvenu à cette relation correcte, on peut être tenté de substituer $X$ par $A$ et de conclure. Ce raisonnement est tout aussi faux que le précédent, puisqu'on a encore à donner un sens à $A I n$ et à $p (A) I n$ .

Un raisonnement plus sophistiqué, mais encore faux

On peut repartir de (1), en le voyant comme une identité entre polynômes de degré $n$ en l'indéterminée $X$ , et à coefficients matriciels, de la forme

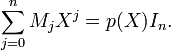$\sum_{j=0}^n M_j X^j=p(X)I_n.$ (2)

La substitution devrait alors consister à remplacer $M j X j$ par $M j A j$ . ce qui est justifié. Mais le premier membre de (2) est un produit de polynômes $P (X) Q (X)$ , et s'il est correct dans l'anneau $\mathcal{M}_n(\mathbb{K})[X]$ d'écrire $P j X j Q k X k = P j Q k X j + k$ , cette relation est généralement fausse si on substitue $X$ par $A$ . Pour qu'elle soit correcte, il faudrait que $Q k$ commute avec $A$ , ce qui n'a pas de raison d'être vrai. 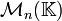Une manière plus abstraite de dire les choses est que, contrairement au cas scalaire, il n'y a pas d'homomorphisme d'évaluation envoyant $\mathcal{M}_n(\mathbb{K})[X]$ sur $\mathcal{M}_n(\mathbb{K})$ en assignant $A$ comme image de $X$ , à moins que la matrice $A$ appartienne au centre de 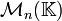$\mathcal{M}_n(\mathbb{K})$ , c'est à dire à l'ensemble des matrices scalaires.

On peut préciser les choses sur un exemple concret. On considère la matrice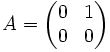

$A=\begin{pmatrix}0&1\\0&0\end{pmatrix}$ ,

dont le polynôme caractéristique est $p (X) = X 2$ ; la matrice complémentaire de $X I 2 - A$ est $X I 2 + A$ ; l'équation (1) devient donc

(X I 2 - A)(X I 2 + A) = X 2 I 2

.(3)

Bien sûr on peut substituer la matrice $A$ à $X$ dans cette identité, puisque le théorème de Cayley-Hamilton est vrai, et ce n'est pas ainsi qu'on pourrait réfuter la méthode proposée : la substitution dans l'identité (3) doit être correcte quelle que soit la matrice que l'on substitue. Si la méthode par substitution était correcte, on aurait $(B - A)(B + A) = B 2$ , ou encore, après simplification et en tenant compte de $A 2 = 0$ , $B A - A B = 0$ . Cette relation devrait être vérifiée quelle que soit la matrice $B$ , or il y a des matrices qui ne commutent pas avec $A$ , par exemple sa transposée.

Aussi abstrait que faux

L'ensemble $\mathbb{K}[X]^n$ des vecteurs colonne à coefficients polynômiaux est un module sur l'anneau $\mathbb{K}[X]$ : si on multiplie un élément de $\mathbb{K}[X]^n$ par un polynôme à coefficient dans $\mathbb{K}$ , on obtient encore un élément de $\mathbb{K}[X]^n$ .

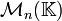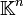La matrice $A$ fournit un homomorphisme de $\mathbb{K}[X]$ dans l'anneau $\mathcal{M}_n(\mathbb{K})$ , qui envoie $X$ sur $A$ ; c'est l'homomorphisme d'évaluation qu'on a déjà défini. Il y a également un homomorphisme d'évaluation de $\mathbb{K}[X]^n$ dans $\mathbb{K}^n$ : si $v\in \mathbb{K}[X]^n$ est donné par

$v(X)=\sum_{j=0}^m v_j X^j,$

on pose

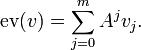$\textrm{ev}(v)=\sum_{j=0}^m A^j v_j.$ (4)

On multiplie l'identité (1) à droite par un vecteur arbitraire 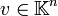$v\in \mathbb{K}^n$ , ce qui fournit

(X I n - A)Comp(X I n - A) v = p (X) v,

qui est une identité dans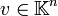 $v\in \mathbb{K}^n$ . Il n'y a plus qu'à appliquer $ev$ aux deux membres de la relation (4), et le tour est joué... sauf qu'on a encore cédé à la tentation de remplacer $X I n$ par $A I n$ , et qu'on a fait semblant de savoir que $ev(M (X) N (X) v) = ev((M N)(X) v)$ .

Le bout du tunnel

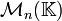
Enfin on peut accroître la confusion en définissant une autre application d'évaluation $Ev A$ de $\mathcal{M}_n(\mathbb{K}[X])$ dans $\mathcal{M}_n(\mathbb{K})$

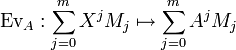$\textrm{Ev}_A:\sum_{j=0}^m X^j M_j \mapsto \sum_{j=0}^m A^jM_j$ (5)

qui enverrait $X I n - A$ sur la matrice nulle.

Le problème est que $Ev A$ n'est pas un homomorphisme d'anneaux (mais seulement une application $K$ -linéaire), parce que $Ev A ((X j M).(X k N))$ n'est en général pas égal à $E v A (X j + k M N)$ , toujours à cause de l'absence de commutativité dans les anneaux de matrices.

Mais dans notre cas, les coefficients du polynôme $X I n - A$ commutent avec $A$ , si bien que l'évaluation du produit est tout a fait justifiée, comme la suite de l'article va le montrer.

Une preuve

Toutes les tentatives de preuves sans effort ont échoué, donc il faut travailler pour de vrai quelque part. Partons de (1), en écrivant

$\textrm{Comp}(XI_n-A)=\sum_{j=0}^{n-1}B_j X^j$

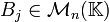avec $B_j\in\mathcal{M}_n(\mathbb{K})$ , et

$p(X)=\sum_{j=0}^n p_jX^j.$

On peut développer le produit $(X I n - A)Comp(X I n - A)$ :

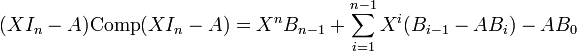$(XI_n-A)\textrm{Comp}(XI_n-A)=X^{n}B_{n-1} +\sum_{i=1}^{n-1}X^i(B_{i-1}-AB_{i}) -AB_0$ ,(6)

qui est identique à

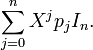$\sum_{j=0}^n X^jp_jI_n.$ (7)

Si on remplace dans le deuxième membre de (6) $X$ par $A$ , en laissant les $A$ à gauche, on voit qu'on a une somme télescopique qui s'annule. La même substitution dans (7) fournit $p (A)$ , et maintenant, la démonstration est correcte.

Une variante

On peut également aligner des idées abstraites dans le même esprit que celles qui ont échoué dans la tentative « aussi abstraite que fausse » mais fournir une preuve juste.

Commençons par introduire un morphisme d'évaluation approprié à la résolution du problème. Tout d'abord, $\mathbb{K}[A]$ étant une algèbre commutative sur $\mathbb{K}$ , on a un morphisme d'évaluation : $\mathbb{K}[X] \to \mathbb{K}[A]$ (qui envoie $X$ sur $A$ et $λ$ sur $λ I n$ pour tout scalaire $λ$ ). Ce morphisme d'anneaux commutatifs induit un morphisme d'évaluation sur les anneaux de matrices $\mathcal{M}_n(\mathbb{K}[X]) \to \mathcal{M}_n(\mathbb{K}[A])$ .

Une notation auxiliaire nous sera utile : pour deux matrices carrées $(n, n)$ notées $C = (c i j)$ et $D = (d i j)$ , on notera 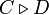$C \triangleright D$ la matrice à coefficients matriciels de terme général $c i j D$ . Si le lecteur connaît le produit de Kronecker de deux matrices, il pourra remarquer que 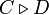$C\triangleright D$ c'est presque la même chose que 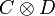$C\otimes D$ à ceci près que 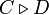$C\triangleright D$ est une matrice $(n, n)$ dont les coefficients sont des matrices $(n, n)$ tandis que 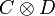$C\otimes D$ est une matrice $(n 2, n 2)$ . Les formules ci-dessous ne contiennent de fait que deux cas particuliers de cette opération : des produits de la forme 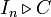$I_n \triangleright C$ c'est-à-dire des matrices carrées avec des $C$ sur la diagonale et des $0$ ailleurs et un produit 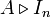$A\triangleright I_n$ c'est-à-dire une variante de $A$ où la matrice $a i j I n$ vient remplacer le coefficient $a i j$ .

Cette notation posée, appliquons le morphisme d'évaluation à la relation :

$(XI_n-A)\,\textrm{Comp}(XI_n-A)=p(X)I_n.$

On obtient une relation

$(I_n\triangleright A-A\triangleright I_n)\,M=I_n\triangleright p(A)\qquad(*)$

dans laquelle $M$ est une certaine matrice à coefficients dans $\mathbb{K}[A]$ dont on n'aura besoin de rien savoir.

Ainsi on a écrit une formule juste, et on en pâtit : on n'a du coup pas fini, l'évaluation de $X I n - A$ par une technique rigoureuse ne fournit pas $0$ mais une bizarre matrice à coefficients matriciels.

Il faut une deuxième idée pour conclure. Elle consiste à remarquer que si 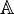$\mathbb{A}$ est un anneau et $E$ un 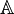$\mathbb A$ -module à droite, pour tous entiers $r$ , $s$ , $t$ on peut définir par les formules habituelles un produit matriciel :

$\mathcal{M}_{rs}(E)\times\mathcal{M}_{st}(\mathbb{A})\to\mathcal{M}_{rt}(E)$

pour laquelle on a associativité si on veut calculer des produits à trois termes :

$\mathcal{M}_{rs}(E)\times\mathcal{M}_{st}(\mathbb{A})\times\mathcal{M}_{tu}(\mathbb{A})\to\mathcal{M}_{ru}(E).$

Appliquons cette notion à 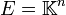$E=\mathbb{K}^n$ (pour les puristes à 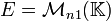$E=\mathcal{M}_{n1}(\mathbb{K})$ ) qui est un module (dont la multiplication s'écrit spontanément à gauche mais peut l'être à droite si on préfère, l'anneau étant commutatif) sur l'anneau commutatif 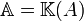$\mathbb{A}=\mathbb{K}(A)$ , la multiplication externe étant l'application : 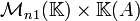$\mathcal{M}_{n1}(\mathbb{K})\times\mathbb{K}(A)$ définie par 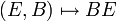$(E,B)\mapsto BE$ (ce $BE\,$ 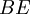étant le produit matriciel ordinaire de la matrice carrée 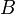$B\,$ par la matrice colonne $E\,$ ).

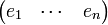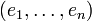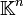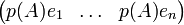Multiplions à gauche la relation $( * )$ par le vecteur ligne $\begin{pmatrix}e_1&\cdots&e_n\end{pmatrix}$ où $(e_1,\ldots,e_n)$ désigne la base canonique de $\mathbb{K}^n$ : en utilisant l'expression de droite dans $( * )$ on obtient le vecteur ligne $\begin{pmatrix}p(A)e_1&\ldots&p(A)e_n\end{pmatrix}$ .

Si maintenant on utilise l'expression de gauche dans $( * )$ et qu'on déplace les parenthèses par associativité de la multiplication matricielle un peu inhabituelle décrite ci avant, on est amené à calculer le produit :

$\begin{pmatrix}e_1&\ldots&e_n\end{pmatrix}(I_n\triangleright A-A\triangleright I_n).$

Pour chaque indice $j$ , on ne peut que constater que sa $j$ -ème composante vaut :

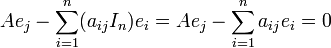$Ae_j-\sum_{i=1}^n(a_{ij}I_n)e_i=Ae_j-\sum_{i=1}^na_{ij}e_i=0$ .

En multipliant ceci à droite par l'inoffensive matrice $M$ et en comparant les deux expressions du produit, on conclut que pour tout indice $j$ , $p (A) e j = 0$ .

Et donc $p (A) = 0$ ^[1].

Remarques additionnelles sur la démonstration

La preuve qui a été donnée évite la substitution de $X$ par une matrice dans un contexte non commutatif, mais les manipulations effectuées sont quand même proches de cette idée : on a bien décomposé l'équation en composantes suivant les puissances de $X$ , on a multiplié à gauche par $A j$ la composante qui était en facteur de $X j$ , et on a additionné tout ensemble. 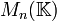En fait, on a utilisé l'opération $Ev A$ définie en (5), sans supposer qu'il s'agisse d'un homomorphisme d'anneaux, de $\mathcal{M}_n(\mathbb{K})[X]$ dans ${M}_n(\mathbb{K})$ . L'opération $Ev A$ est une évaluation à gauche, parce que la multiplication par l'indéterminée scalaire $X$ est remplacée par la multiplication à gauche par $A$ .

Une autre observation est importante : la forme exacte du polynôme $Comp(X I n - A)$ n'a aucune importance. Il y a donc quelque chose à exploiter ici, ce que n'ont pas manqué de faire les mathématiciens.

Soit $M$ un anneau non commutatif ; on peut définir une division euclidienne d'un polynôme $P\in M[X]$ par un polynôme $B$ monique. C'est un polynôme dont le coefficient du terme de plus haut degré est une unité de $M$ , c'est à dire un élément de $M$ qui possède un inverse dans $M$ . Plus précisément, il existe deux polynômes $Q, R\in M[X]$ , avec $R$ de degré strictement inférieur au degré de $B$ , tels que

P = B Q + R .

La démonstration est entièrement analogue à celle du cas scalaire. Si $B = X I n - A$ , alors le reste $R$ est de degré $0$ , et donc identique à une constante appartenant à $M$ . Mais dans ce cas, en raisonnant exactement comme dans la démonstration du théorème de Cayley-Hamilton, on arrive à la conclusion

Ev A (P) = R

Il s'ensuit que $Ev A (P)$ est nul si et seulement si $P$ est divisible à gauche par $X I n - A$ .

La démonstration du théorème de Cayley-Hamilton donne aussi une autre information : le polynôme $Comp(X I n - A)$ est le quotient à gauche de $p (X) I n$ par $t I n - A$ . Comme $p (X) I n$ et $X I n - A$ appartiennent tous deux au sous-anneau commutatif $K[A][X]$ , la division à gauche se passe entièrement dans ce sous-anneau, c'est donc une division ordinaire. En particulier, les coefficients matriciels de $Comp(X I n - A)$ sont des combinaisons linéaires de puissances de $A$ . En d'autres termes, la matrice complémentaire d'une matrice $A$ est un polynôme en $A$ , ce qu'il n'est pas facile de déduire directement de la définition d'une matrice complémentaire. Mieux, on peut calculer explicitement ses coefficients à partir de ceux du polynôme caractéristique $p (X)$ , puisqu'il s'agit de faire une division euclidienne ordinaire, et on trouve

$\textrm{Comp(-A)}=\sum_{j=1}^n p_jA^{j-1}.$

On aurait pu également obtenir cette relation directement à partir du théorème de Cayley-Hamilton, en vertu de l'identité

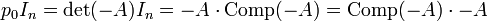$p_0I_n=\det(-A)I_n=-A\cdot \textrm{Comp}(-A)=\textrm{Comp}(-A)\cdot-A$ .

Abstraction et généralisations

La preuve donnée ci-dessus n'utilise que les propriétés d'anneau commutatif du corps $\mathbb{K}$ . La règle de Cramer reste valide pour une matrice à coefficients dans n'importe quel anneau commutatif $B$ . On peut donc généraliser le théorème de Cayley-Hamilton à ce cas, en utilisant la règle de Cramer pour des matrices à coefficients dans l'anneau $B = R [X]$ , $R$ étant un anneau commutatif quelconque.

Dans un cadre encore plus abstrait, si $M$ est un module libre de type fini sur un anneau commutatif $R$ , le théorèmde de Cayley-Hamilton continue à fonctionner. Mieux, si $φ$ est un endomorphisme d'un $R$ -module $M$ de de type fini, on peut définir le polynôme caractéristique de $φ$ comme suit : soient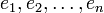 $e_1, e_2,\dots, e_n$ une famille de générateurs de $M$ . On peut trouver des éléments $a i j$ de $R$ tels que

$\phi(e_i)=\sum_{j=1}^n a_{ij}e_j.$

Les coefficients $a i j$ ne sont pas uniquement déterminés, puisqu'on n'a pas supposé libre la famille des $e i$ . Néanmoins, si on note $A$ la matrice 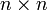$n\times n$ formée de ces coefficients, on peut montrer que le polynôme $p (X) = det(X I n - A)$ ne dépend pas du choix des $a i j$ , mais seulement de l'endomorphisme $φ$ . De même, on peut définir la matrice complémentaire de l'endomorphisme $φ$ et établir une version généralisée de la règle de Cramer.

Dans ce cas, le théorème de Cayley-Hamilton est toujours vrai, et la conclusion est $p (φ) = 0$ . La preuve donnée plus haut continue à fonctionner, puisqu'elle ne comporte pas de division par des éléments de $\mathbb{K}$ , et donc dans le cas présent de division par des éléments de $R$ . Cette version plus générale est la source du célèbre lemme de Nakayama en géométrie algébrique.

Références

(en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Cayley-Hamilton Theorem ».

↑ Cette preuve est celle qui figure dans Introduction to commutative algebra, M. F. Atiyah et I. G. Macdonald, Addison-Wesley, (ISBN 0-201-00361-9), p. 21.

Voir aussi

Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Colinéarité • Indépendance linéaire • Famille libre • Rang • Famille génératrice • Base • Théorème de la base incomplète
Sous-espace	Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension d'un espace vectoriel • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Endomorphisme nilpotent
En dimension finie	Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Cayley-Hamilton ».

Catégories : Application linéaire | Polynôme | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Cayley-Hamilton de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Théorème de cayley-hamilton — Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace vectoriel de dimension finie sur… … Wikipédia en Français
théorème de Cayley-Hamilton — ● théorème de Cayley Hamilton Théorème selon lequel tout endomorphisme d un K espace vectoriel de dimension n ou toute matrice A de Mn(K) annule son polynôme caractéristique P, soit P(f) = 0 ou P(A) = 0 … Encyclopédie Universelle
Théorème de Cayley-Hamilton — Ne pas confondre avec le théorème de Cayley en théorie des groupes ni avec le théorème d Hamilton en géométrie. En algèbre linéaire, le théorème de Cayley Hamilton affirme que tout endomorphisme d un espace vectoriel de dimension finie sur… … Wikipédia en Français
Cayley-Hamilton — Théorème de Cayley Hamilton Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace… … Wikipédia en Français
Théorème de Hamilton-Cayley — Théorème de Cayley Hamilton Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace… … Wikipédia en Français
Theoreme de la base incomplete — Théorème de la base incomplète Le théorème de la base incomplète énonce que toute famille libre de vecteurs d un espace vectoriel E peut être complétée pour obtenir une base de E. Sommaire 1 Enoncé 2 Démonstration 2.1 … Wikipédia en Français
Théorème de Baire-Brenef — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… … Wikipédia en Français
Théorème d'Hamilton — Ne pas confondre avec le théorème de Cayley Hamilton en algèbre linéaire. Le théorème d Hamilton est un théorème de géométrie du triangle, dû à William Rowan Hamilton : Soit ABC un triangle et O son orthocentre. Les triangles ABC, ABO … Wikipédia en Français
Théorème du rang — En mathématiques, et plus précisément en algèbre linéaire, le théorème du rang lie le rang d une application linéaire et la dimension de son noyau. Il peut être vu comme un cas particulier de théorème d isomorphisme, ou être interprété par la… … Wikipédia en Français
Théorème de la base incomplète — En algèbre linéaire, le théorème de la base incomplète affirme que, dans un espace vectoriel E, toute famille libre de vecteurs peut être complétée en une famille libre et génératrice de E (c est à dire une base de E) ; de toute famille… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Theoreme de Cayley-Hamilton

Théorème de Cayley-Hamilton

Sommaire

Motivation

Exemple