Theoreme de representation de Riesz

Theoreme de representation de Riesz: Théorème de représentation de Riesz

Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l'honneur du mathématicien Frigyes Riesz.

Sommaire

1 Le théorème de représentation de Riesz dans les espaces de Hilbert

1.1 Énoncé

1.2 Démonstration

1.2.1 Existence de y

1.2.2 Unicité de y

1.3 Remarque

1.4 Extension aux formes bilinéaires

1.4.1 Énoncé

1.4.2 Démonstration

2 Le théorème de représentation de Riesz en théorie de la mesure

2.1 Énoncé

3 Notes et références

Le théorème de représentation de Riesz dans les espaces de Hilbert

Ce théorème est aussi parfois appelé théorème de Fréchet-Riesz.

Énoncé

Soient :

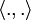
$H$ un espace de Hilbert muni de son produit scalaire noté $\langle.,.\rangle$

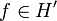$f \in H'$ une forme linéaire continue sur $H$ .

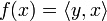Alors il existe un unique $y$ dans $H$ tel que pour tout $x$ de $H$ on ait $f(x)=\langle y,x\rangle$ .
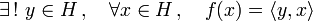
$\exists\,!\ y \in H\,, \quad \forall x\in H\,, \quad f(x) = \langle y,x\rangle$
Démonstration

$ker(f)$ (noyau de l'application linéaire $f$ ) est un sous-espace vectoriel de $H$ . De plus comme $f$ est continue, $ker(f)$ est fermé car c'est l'image réciproque du fermé ${0}$ .

Existence de $y$

Si 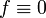$f\equiv 0$ , il suffit de choisir $y = 0$ .

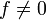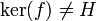Supposons $f\ne 0$ , on a alors $\ker(f)\ne H$ .

$ker(f)$ est fermé, on peut donc appliquer le théorème du supplémentaire orthogonal d'un fermé dans un espace de Hilbert, qui montre que :
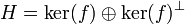$H = \ker(f) \oplus \ker(f)^\bot$ .
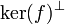Explicitons une projection sur $\ker(f)^\bot$ :

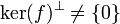De ce qui précède on déduit que $\ker(f)^\bot\ne\big\{ 0 \big\}$ .

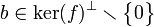Soit donc $b \in \ker(f)^\bot \smallsetminus \big\{0\big\}$ ,

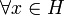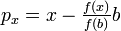$\forall x \in H$ , posons $p_x=x-\tfrac{f(x)}{f(b)}b$ .

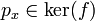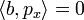Ainsi $p_x \in \ker(f)$ et en particulier $\langle b,p_x\rangle = 0$ .

En développant, on obtient
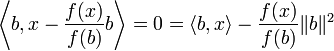
$\left\langle b, x-{f(x) \over f(b)}b \right\rangle = 0 = \langle b, x\rangle - {f(x) \over f(b)} \| b \|^2$
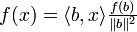D'où $f(x) = \langle b, x\rangle \tfrac{f(b)}{\|b\|^2}$ .

On a finalement
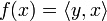
$f(x) = \langle y, x \rangle$
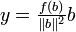avec $y = \tfrac{f(b)}{\|b\|^2}b$ .

Unicité de $y$

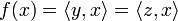Soient $y$ et $z$ deux éléments de $H$ vérifiant $f(x) = \langle y, x \rangle = \langle z, x \rangle$ .

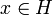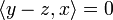Pour tout $x \in H$ on a $\langle y-z, x \rangle = 0$ et en particulier 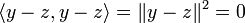$\langle y-z, y-z \rangle = \|y-z\|^2 = 0$ d'où $y = z$ .

Remarque

De plus
$\|y\|=\|f\|^'$
.

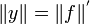
Extension aux formes bilinéaires

Énoncé

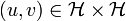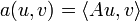Si $a$ est une forme bilinéaire continue sur un espace de Hilbert $\mathcal{H}$ , alors il existe un unique endomorphisme de $\mathcal{H}$ , linéaire et continu que l'on note $A$ , tel que, pour tout $(u,v)\in \mathcal{H}\times\mathcal{H}$ on ait $a(u,v)=\langle Au,v \rangle$ .
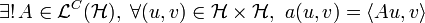
$\exists !\,A\in\mathcal{L}^{C}(\mathcal{H}),\ \forall (u,v)\in\mathcal{H}\times\mathcal{H},\ a(u,v)=\langle Au,v \rangle$
Démonstration

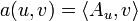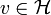Pour un élément $u$ de $\mathcal{H}$ fixé, le théorème de représentation de Riesz assure de l'existence d'un unique $A u$ dans $\mathcal{H}$ tel que $a(u,v)=\langle A_u,v\rangle$ pour tout $v\in\mathcal{H}$ .

On pose 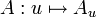$A:u\mapsto A_u$ défini tel que décrit ci-dessus. Pour tous $v, u 1, u 2$ de $\mathcal{H}$ et tout réel $λ$ on a
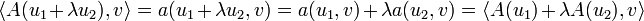
$\langle A(u_1+\lambda u_2),v\rangle=a(u_1+\lambda u_2,v)=a(u_1,v)+\lambda a(u_2,v)=\langle A(u_1)+ \lambda A(u_2),v\rangle$
donc $A$ est linéaire.

La forme $a$ est continue, donc lipschitzienne. Soit $c$ une constante de Lipschitz de $a$ .
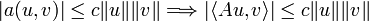$|a(u,v)|\le c\|u\| \|v\| \Longrightarrow |\langle A u,v \rangle|\le c\|u\| \|v\|$ .
Pour $v = A u$ , on a 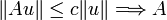$\|A u\|\le c\|u\| \Longrightarrow A$ continu.

Le théorème de représentation de Riesz en théorie de la mesure

Le théorème de représentation de Riesz est fondamental en théorie de la mesure, et permet entre autres une construction efficace de la mesure de Lebesgue à partir de l'intégrale de Riemann. Il est connu que l'intégrale sur un espace topologique $X$ associée à une mesure de Borel quelconque $μ$ est une forme linéaire positive sur l'espace vectoriel $C c (X)$ des fonctions réelles, continues et à support compact définies sur $X$ . Le théorème de représentation de Riesz établit sous certaines hypothèses la réciproque de cette propriété : on se donne une forme linéaire sur $C c (X)$ , et on veut savoir si elle correspond à l'intégrale associée à une mesure $μ$ .

Énoncé

Soit $X$ un espace séparé localement compact, et soit $Λ$ une forme linéaire positive sur $C c (X)$ . Alors il existe une tribu 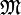$\mathfrak{M}$ contenant les boréliens, et une unique mesure $μ$ sur 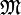$\mathfrak{M}$ telles que :

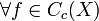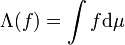
$\forall f \in C_c(X)$ , $\Lambda(f) = \int f\mathrm d\mu$

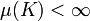
Pour tout compact $K$ de X, $\mu(K)<\infty$

Pour tout $E\in\mathfrak{M}$ , $\mu(E)=\inf \{\mu(V), E\subset V {\rm ouvert}\}$

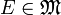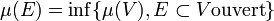
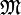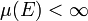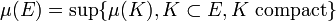
Pour tout $E$ ouvert de $X$ ou appartenant à $\mathfrak{M}$ et vérifiant $\mu(E)<\infty$ , $\mu(E)=\sup\{\mu(K), K\subset E, K \text{ compact}\}$

La mesure $μ$ est construite comme suit^[1] :

Pour tout ouvert $V$ de X, on pose 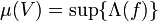$\mu(V) = \sup\{\Lambda(f)\}$ où $f$ décrit l'ensemble des fonctions à valeurs dans [0,1] et dont le support est compact et inclus dans $V$ .

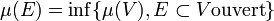
Pour toute partie $E$ de $X$ , on pose $\mu(E) = \inf\{\mu(V), E \subset V {\rm ouvert }\}$

La tribu 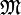$\mathfrak{M}$ est constituée des parties $E$ de $X$ telles que, pour tout compact $K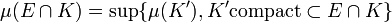$ , $\mu(E \cap K) = \sup\{\mu(K'), K' {\rm compact } \subset E \cap K \}$

Notes et références

↑ Walter Rudin, Analyse réelle et complexe : cours et exercices [détail des éditions]

Articles de mathématiques en rapport avec l'algèbre bilinéaire

Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz

modifier

Articles de mathématiques en rapport avec l'analyse fonctionnelle

Fonctionnelle • Calcul des variations • Dérivée fonctionnelle • Espace de Banach • Algèbre de Banach • Espace de Hilbert • Espace de Fréchet • Variété banachique • Espace de fonctions • Noyau reproduisant • Série de Fourier • Transformée de Fourier • Distribution • Topologie faible

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de repr%C3%A9sentation de Riesz ».

Catégories : Espace de Hilbert | Théorème de mathématiques

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de representation de Riesz de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Théorème de représentation de riesz — Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz dans les espaces de Hilbert 1.1 Énoncé 1.2 … Wikipédia en Français
Théorème de représentation de Riesz — Pour les articles homonymes, voir Théorème de Riesz. Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz … Wikipédia en Français
Théorème de Fréchet-Riesz — Théorème de représentation de Riesz Il existe en analyse fonctionnelle plusieurs théorèmes nommés théorème de représentation de Riesz, en l honneur du mathématicien Frigyes Riesz. Sommaire 1 Le théorème de représentation de Riesz dans les espaces … Wikipédia en Français
Theoreme de Riesz — Théorème de Riesz En mathématiques, et plus particulièrement en théorie des espaces vectoriels normés réels ou complexes, le théorème de Riesz établit un lien entre la notion de compacité, une propriété topologique, et celle de dimension, une… … Wikipédia en Français
Théorème de riesz — En mathématiques, et plus particulièrement en théorie des espaces vectoriels normés réels ou complexes, le théorème de Riesz établit un lien entre la notion de compacité, une propriété topologique, et celle de dimension, une notion algébrique. Il … Wikipédia en Français
Theoreme de Stampacchia — Théorème de Stampacchia Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
Théorème de stampacchia — Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
Theoreme de Lax-Milgram — Théorème de Lax Milgram Le théorème de Lax Milgram – des noms de Peter Lax et Arthur Milgram – est un théorème de mathématiques. Il est utilisé pour résoudre des équations différentielles partielles via la formulation faible et sert ainsi… … Wikipédia en Français
Théorème de lax-milgram — Le théorème de Lax Milgram – des noms de Peter Lax et Arthur Milgram – est un théorème de mathématiques. Il est utilisé pour résoudre des équations différentielles partielles via la formulation faible et sert ainsi notamment de fondement à la… … Wikipédia en Français
Theoreme spectral — Théorème spectral Un ellipsoïde en trois possède autant d axes de symétrie que l espace de dimensions. Ils sont notés ici x, y et z … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts