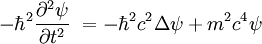- Equation aux derivees partielles
-
Équation aux dérivées partielles
En mathématiques, plus précisément en calcul différentiel, une équation aux dérivées partielles ou équation différentielle partielle (EDP) est une équation dont les solutions sont les fonctions inconnues vérifiant certaines conditions concernant leurs dérivées partielles.
Une EDP a souvent de très nombreuses solutions, les conditions étant moins strictes que dans le cas d'une équation différentielle ordinaire (à une seule variable) ; les problèmes incluent souvent des conditions aux limites qui restreignent l'ensemble des solutions. Alors que les ensembles de solutions d'une équation différentielle ordinaire sont paramétrées par un ou plusieurs paramètres correspondant aux conditions supplémentaires, dans le cas des EDP les conditions aux limites se présentent plutôt sous la forme de fonction ; intuitivement cela signifie que l'ensemble des solutions est beaucoup plus grand, ce qui est vrai dans la quasi-totalité des problèmes.
Les EDP sont omniprésentes dans les sciences, puisqu'elles apparaissent aussi bien en dynamique des structures, mécanique des fluides que dans les théories de la gravitation ou de l'électromagnétisme (équations de Maxwell). Elles sont primordiales dans des domaines tels que la simulation aéronautique, la synthèse d'images, ou la prévision météorologique. Enfin, les équations les plus importantes de la relativité générale et de la mécanique quantique sont également des EDP.
L'un des dix problèmes à un million de dollars proposés par la fondation Clay consiste à montrer l'existence et la continuité par rapport aux données initiales d'un système d'EDP appelé équations de Navier-Stokes. Ces équations servent énormément dans la mécanique des fluides.
Articles d'analyse vectorielle 
Objets d'étude Champ vectoriel Champ scalaire Équation aux dérivées partielles de Laplace de Poisson Opérateurs Nabla Gradient Rotationnel Divergence Laplacien scalaire Bilaplacien Laplacien vectoriel D'alembertien Théorèmes de Green de Stokes de Helmholtz de flux-divergence du gradient du rotationnel Sommaire
Introduction
Une équation différentielle très simple est :
où u est une fonction inconnue de x et y. Cette relation implique que les valeurs u(x,y) sont indépendantes de x. Les solutions de cette équation sont :
où f est une fonction de y. L'équation ordinaire,
a pour solution :
avec c une valeur constante (indépendante de x). Ces deux exemples illustrent qu'en général, les solutions d'une équation différentielle ordinaire met en jeu une constante arbitraire, tandis que les équations aux dérivées partielles mettent en jeu des fonctions arbitraires. Une solution des équations aux dérivées partielles n'est généralement pas unique.
Trois catégories importantes d'EDP sont les équations aux dérivées partielles linéaires et homogènes du second-ordre dites elliptiques, hyperboliques et paraboliques.
Notations
En mathématiques
Pour les EDP, par souci de simplification, il est d'usage d'écrire u la fonction inconnue et Dxu (notation française) ou ux (notation anglo-saxonne, plus répandue) sa dérivée partielle par rapport à x, soit avec les notations habituelles du calcul différentiel :
et pour les dérivées partielles secondes :
En physique
Les opérateurs de l'analyse vectorielle sont utilisés.
Résumé d'analyse vectorielle- L'opérateur nabla
![\left[ \vec{\nabla} = \left(\begin{array}{c} \frac {\partial}{\partial x} \\ \frac {\partial}{\partial y} \\ \frac {\partial}{\partial z}\end{array}\right)\right] \](/pictures/frwiki/55/745da3efc34c7251c66642d0bd3147a5.png) représente le jeu des dérivées partielles d'ordre 1
représente le jeu des dérivées partielles d'ordre 1 - Pour une fonction vectorielle
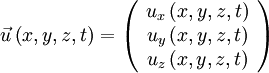 , en lui appliquant le produit scalaire par
, en lui appliquant le produit scalaire par  , on définit la divergence:
, on définit la divergence: 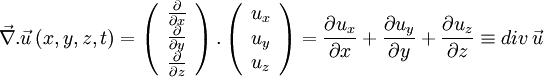
- En utilisant le produit vectoriel, on définit le rotationnel
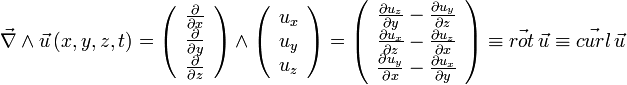
- Pour une fonction qui à tout point de l'espace associe un nombre scalaire,
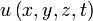 , on définit le gradient:
, on définit le gradient: 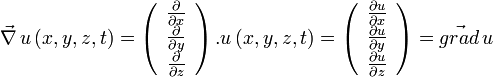
- On utilise également l'opérateur Laplacien , analogue de la divergence pour la dérivation d'ordre 2
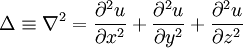
- voir aussi l'opérateur Laplacien vectoriel
Exemples d'EDP
Équation de Laplace
L'équation de Laplace est une EDP de base très importante :
où u(x,y,z) désigne la fonction inconnue.
En notation d'analyse vectorielle, en utilisant l'opérateur laplacien Δ
- Soit
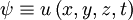 , fonction d'onde.
, fonction d'onde. 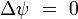
Équation de propagation (ou équation des cordes vibrantes)
Cette EDP décrit les phénomènes de propagation des ondes sonores et des ondes électromagnétiques (dont la lumière). La fonction d'onde inconnue est notée u(x,y,z,t), t représentant le temps :
Le nombre c représente la célérité ou vitesse de propagation de l'onde u.
En notation d'analyse vectorielle, en utilisant l'opérateur laplacien Δ :
- Soit
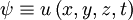 , fonction d'onde.
, fonction d'onde. 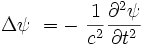
Equation d'onde, forme générale Onde ψ Partie longitudinale Partie transversale Propagation Dissipation Δψ 
![\vec{grad}\left[div \ \psi \right]](/pictures/frwiki/98/b4ef66f9149c8f59ae99585485d3afb2.png)

![\vec{rot}\left[\vec{rot} \ \psi\right]](/pictures/frwiki/100/d7c5d592b4ebd71f20d978c2e251fe15.png)

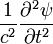
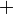
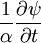
Voir aussi onde sismique, onde mécanique, Son, Onde sur une corde vibrante, Onde stationnaire dans un tuyau, Equations de Maxwell
Équation de Fourier
Cette EDP est également appelée équation de la chaleur. La fonction u représente la température. La dérivée d'ordre 1 par rapport au temps traduit l'irréversibilité du phénomène. Le nombre α est appelé diffusivité thermique du milieu.
En notation d'analyse vectorielle, en utilisant l'opérateur laplacien Δ :
- Soit
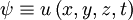 , fonction d'onde de température.
, fonction d'onde de température. 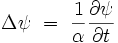
Équation de Poisson
En utilisant l'opérateur laplacien Δ :
- Soient
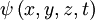 , fonction d'onde et
, fonction d'onde et 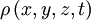 densité de charge.
densité de charge. 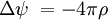
Équation d'onde de Langmuir
- Soient
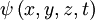 , fonction d'onde et
, fonction d'onde et 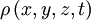 densité de charge.
densité de charge. 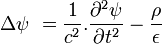
Cette équation décrit des ondes électriques longitudinales en propagation dans un plasma.
Équation de Stokes
L'équation de Stokes décrit l'écoulement d'un fluide newtonien incompressible en régime permanent et à faible nombre de Reynolds, s'écrit :
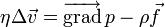 ,
,
Notations :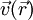 est la vitesse du fluide ;
est la vitesse du fluide ;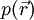 est la pression dans le fluide ;
est la pression dans le fluide ;- ρ est la masse volumique du fluide
- η est la viscosité dynamique du fluide;
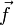 est une force massique s'exerçant dans le fluide (par exemple : pesanteur) ;
est une force massique s'exerçant dans le fluide (par exemple : pesanteur) ;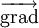 et Δ sont respectivement les opérateurs différentiels gradient et laplacien.
et Δ sont respectivement les opérateurs différentiels gradient et laplacien.
Équation de Schrödinger
Notations :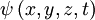 , fonction d'onde.
, fonction d'onde.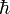 constante de planck réduite.
constante de planck réduite.- m est la masse de la particule.
- i nombre complexe imaginaire tel que i2 = − 1.
- V opérateur potentiel (représente le potentiel en tout point), en général électrique.
- Δ est le laplacien.
Équation de Klein-Gordon
Soit
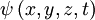 , fonction d'onde.Notations :
, fonction d'onde.Notations :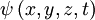 , fonction d'onde.
, fonction d'onde.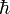 constante de planck réduite.
constante de planck réduite.- m est la masse de la particule.
- c est la vitesse de la lumière
- Δ est le laplacien.
Méthodes de résolution numérique
Les méthodes numériques les plus couramment utilisées pour la résolution des équations aux dérivées partielles sont :
- Méthode des différences finies
- Méthode des éléments finis
- Méthode des volumes finis
- Méthode des caractéristiques
Articles connexes
Bibliographie
- Lars Hörmander ; The analysis of linear partial differential operators, Springer-Verlag (1983 à 1985). Traité de référence en quatre volumes, par le récipiendaire de la médaille Fields 1962. Le volume I est sous-titré : Distribution theory and Fourier analysis, et le volume II : Differential operators with constant coefficients. Les volumes III et IV sont consacrés à la théorie moderne via les opérateurs pseudo-différentiels.
- Lars Hörmander ; Linear Partial Differential Operators, Springer-Verlag (1963). Le livre qui contient les travaux pour lesquels l'auteur a obtenu la médaille Fields en 1962.
- Yu.V. Egorov & M.A. Shubin ; Foundations of the Classical Theory of Partial Differential Equations, Springer-Verlag (2ème édition - 1998), ISBN 3-540-63825-3. Premier volume d'une série qui en comporte neuf, écrits pour l' Encylopaedia of Mathematical Sciences. Les volumes suivants sont consacrés à la théorie moderne via les opérateurs pseudo-différentiels.
- Michael E. Taylor ; Partial Differential Equations - Basic Theory, Series: Texts in Applied Mathematics, Vol. 23, Springer-Verlag (2ème édition - 1999), ISBN 0-387-94654-3. Premier volume d'une série qui en comporte trois. Les volumes suivants sont consacrés à la théorie moderne via les opérateurs pseudo-différentiels.
- Vladimir I. Arnold ; Lectures on partial differential equations, Springer-Verlag (2004), ISBN 3-540-40448-1.
- Portail des mathématiques
Catégories : Analyse à plusieurs variables | Analyse fonctionnelle | Équation aux dérivées partielles
Wikimedia Foundation. 2010.

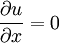
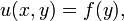
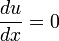
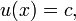
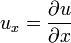
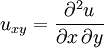
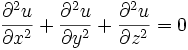
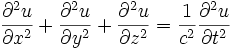
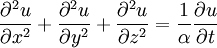
![i\hbar {\part \psi \over \part t} \ = \left[ - \frac{\hbar^2}{2m}\Delta + V\right] \psi](/pictures/frwiki/54/6885c6e97a69f183383d64d72f615caf.png)