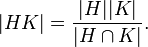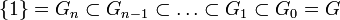- Groupe Fini
-
Groupe fini
En mathématiques, un groupe fini est un groupe constitué d'un nombre fini d'éléments, c'est-à-dire que son cardinal est fini.
Sommaire
Introduction
Soit G un groupe. On note sa loi multiplicativement et 1 son élément neutre, sauf dans le cas où G est abélien, où la loi (resp. l'élément neutre) est notée additivement (respectivement 0).
On dit que G est un groupe fini si son cardinal est fini. Le cardinal est alors noté | G | et est appelé ordre du groupe.
On supposera dans la suite que G est un groupe fini.
Soit . Comme G est fini, le principe de Dirichlet (ou des cages à pigeons) permet de montrer que l'ensemble
. Comme G est fini, le principe de Dirichlet (ou des cages à pigeons) permet de montrer que l'ensemble 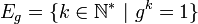 est non vide. Il admet donc un plus petit élément, que l'on appelle l'ordre de g.
est non vide. Il admet donc un plus petit élément, que l'on appelle l'ordre de g.Attention au risque de confusion, ici le terme ordre désigne successivement deux concepts différents, mais il y a quand même un lien, voir ci dessous (groupe cyclique).
L'ordre d d'un élément g possède une propriété arithmétique très utile (qui provient directement de la division euclidienne) :
-
-
- Soit n un entier non nul tel que gn = 1 alors d divise n.
-
Un sous-ensemble S de G engendre ce groupe si tous les éléments de G s'écrivent comme un produit d'éléments ou d'inverse d'éléments de S. L'ensemble S est appelé une partie génératrice de G.
Comme G est fini, l'inverse d'un élément g est une puissance de g (plus précisément, on a g − 1 = gd − 1, où d désigne l'ordre de g). Il suit donc qu'un sous-ensemble S de G est une partie génératrice si et seulement si tout élément de G est un produit d'éléments de S.
Un groupe fini engendré par un singleton {g} est dit cyclique. Par abus de langage, on dit que l'élément g engendre G, et on note alors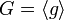 . Il est facile de vérifier qu'un tel groupe est nécessairement abélien.
. Il est facile de vérifier qu'un tel groupe est nécessairement abélien.Remarquons que dans ce cas, l'ordre de G est égal à l'ordre d'un de ses générateurs.
Tous les éléments d'un groupe fini G ont un ordre inférieur ou égal à | G | .Un résultat fondamental dans l'étude des groupes finis est le théorème de Lagrange :
-
-
- Soit G un groupe fini et H un sous-groupe de G, alors l'ordre de H divise l'ordre de G.
-
Une conséquence immédiate est que si G est un groupe fini, si m=|G|, alors si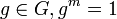 . (considérer le sous-groupe engendré par g)
. (considérer le sous-groupe engendré par g)Parité de l'ordre et involution
L'ordre d'un groupe fini qui n'a pas d'involution (élément d'ordre 2) est impair, en effet le nombre d'éléments différents du neutre est pair.
Réciproquement si son ordre est impair il n'a pas d'involution, en effet s'il possède au moins une involution, d'après le Théorème de Lagrange, son ordre est pair.
En conclusion l'ordre d'un groupe fini est
- impair ssi il n'a pas d'involution.
- pair ssi il possède au moins une involution.
Dans le cas où l'ordre est pair le nombre d'involution(s) est impair.
Exemples
Voici quelques exemples classiques de groupes finis:
- Groupe des racines n-ièmes de l'unité :
 où
où 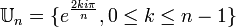 ;
;
- Les classes résiduelles modulo n :
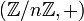 ;
;
- Les groupes symétriques :
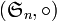 groupes des bijections d'un ensemble fini dans lui-même ;
groupes des bijections d'un ensemble fini dans lui-même ;
- Groupes diédraux,
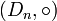 : groupes des isométries planes qui conservent un polygone régulier à n côtés;
: groupes des isométries planes qui conservent un polygone régulier à n côtés;
- Le groupe de Klein.
Les deux premiers exemples désignent en fait le même groupe. Pour comprendre ce qu'on entend par même, on va introduire la notion de morphisme de groupe.Morphismes de groupes
Consulter aussi l'article détaillé homomorphisme de groupe
Lorsque deux groupes sont isomorphes, ils sont identiques du point de vue de la théorie des groupes.
L'étude des morphismes de groupes est donc importante pour la compréhension des groupes. Des branches de la théorie des groupes finis, comme la théorie des représentations d'un groupe fini, sont consacrées entièrement à cette activité.
Par exemple, les groupes
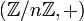 et
et  sont isomorphes.
sont isomorphes.Pour le montrer, il suffit de vérifier que l'application
 définie par
définie parest un isomorphisme de groupe.
Dire que ces groupes sont isomorphes signifie qu'ils sont identiques : toutes les propriétés de l'un se retrouvent dans l'autre. Dans la théorie des groupes, on n'étudiera donc les propriétés que d'un seul de ces deux groupes (celui qu'on veut).
Théorème de Wilson
Dans un groupe abélien fini le produit des éléments est égal
- au neutre si son ordre est impair
- au produit des involutions si son ordre est pair
Pour le groupe
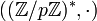 , avec p premier impair, on retrouve le Théorème de Wilson classique.
, avec p premier impair, on retrouve le Théorème de Wilson classique.En effet, l'ordre, qui est égal à p − 1, est pair et l'unique involution est p − 1.
Produit direct - Produit semi-direct
À partir de deux groupes finis H et K, on peut construire un nouveau groupe : le produit direct externe de H par K ; plus généralement, si l'on se donne en plus un morphisme
 , alors on peut construire le produit semi-direct externe de H par K suivant f. Ce sont des groupes finis, de cardinal | H | | K | .
, alors on peut construire le produit semi-direct externe de H par K suivant f. Ce sont des groupes finis, de cardinal | H | | K | .Une question naturelle se pose alors : si G est un groupe, à quelle condition G est-il un produit direct interne (ou un produit semi-direct interne) de deux sous-groupes H et K ?
Donnons un critère répondant à cette question. On pose
 (attention, ce sous-ensemble de G n'est en général pas un groupe).
(attention, ce sous-ensemble de G n'est en général pas un groupe).
Produit direct interneUn groupe G est produit direct interne de deux sous-groupes H et K si et seulement si :
-
-
- Les groupes H et K sont distingués dans G,
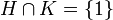 ,
,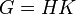 .
.
-
Produit semi-direct interneUn groupe G est produit semi-direct interne de deux sous-groupes H et K si et seulement si :
-
-
- Le groupe H est distingué dans G,
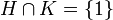 ,
,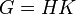 .
.
-
Lorsque G est fini, on peut s'aider de l'égalité combinatoire suivante :Ainsi, dans le cas où G est fini, les deux critères se voient considérablement simplifiés. En effet si les deux premiers points du critère sont vérifiés, alors le troisième point peut être remplacé par | G | = | H | | K | .
Parmi les exemples donnés ci-dessus, on peut montrer que le groupe de Klein est isomorphe au produit direct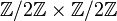 . Le groupe diédral est quant à lui isomorphe au produit semi-direct de
. Le groupe diédral est quant à lui isomorphe au produit semi-direct de 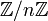 par
par 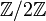 .
.On a vu que tout groupe cyclique est abélien. Le groupe de Klein montre que la réciproque est fausse. On a cependant le résultat remarquable suivant :
-
- Tout groupe abélien fini est un produit direct de groupes cycliques.
Sous-groupes de Sylow
Soit G un groupe fini d'ordre n, soit p un diviseur premier de n, soit pr la plus grande puissance de p qui divise n, de sorte que n = prm, m étant un entier non divisible par p. On appelle p-sous-groupe de Sylow de G tout sous-groupe d'ordre pr de G.
On démontre les énoncés suivants (théorèmes de Sylow) :- tout p-sous-groupe de G, c'est-à-dire tout sous-groupe de G dont l'ordre est une puissance de p, est contenu dans au moins un p-sous-groupe de Sylow de G; il en résulte que les p-sous-groupes de Sylow de G sont les éléments maximaux de l'ensemble des p-sous-groupe de G, ce par quoi certains auteurs les définissent ;
- les p-sous-groupe de Sylow de G sont conjugués entre eux ;
- leur nombre est congru à 1 modulo p ;
- ce nombre divise le facteur m défini plus haut.
Les sous-groupes de Sylow sont un instrument essentiel de l'étude des groupes finis.
Classification des groupes finis
On rencontre de nombreuses structures de groupes finis de nature très différentes. À ce titre, l'étude des groupes finis est riche et compliquée. Une approche naturelle pour aborder cette théorie serait de donner une classification des groupes finis, c’est-à-dire, une liste de familles de groupes décrivant, à isomorphisme près, tous les groupes finis. Ce problème est très ardu. On est d'ailleurs actuellement incapable de produire une telle liste.
Apportons tout de même quelques éléments de réponses. Dans le cas où le groupe est abélien, la théorie est parfaitement connue. Elle se généralise même aux groupes abéliens de type fini. Sinon, on introduit des groupes d'un type particulier: les groupes simples . On va tenter de saisir le rôle primordial qu'ils ont et comprendre comment, dans une certaine mesure, ils permettent d'appréhender la classification des groupes finis. Auparavant, on a besoin d'introduire quelques notions.
Soit G un groupe fini, on appelle suite normale de G toute suite finie strictement décroissante (au sens de l'inclusion) de sous-groupes:telle que Gi est un sous-groupe distingué de Gi − 1.
Une suite normale est dite de décomposition si elle est maximale. Le groupe Gi étant distingué dans Gi − 1, il y a un sens à considérer le groupe quotient Gi − 1 / Gi (noté Fi dans la suite). Les groupes Fi qui apparaissent dans cette construction sont appelés les facteurs de décomposition de la suite. La maximalité de la suite de décomposition entraîne immédiatement qu'ils sont simples.
Par ailleurs, un théorème de Jordan-Hölder affirme que deux suites de décomposition de G ont (à isomorphisme près) les mêmes facteurs de décomposition. (Attention, ils peuvent ne pas apparaître dans le même ordre).
-
-
- Ainsi, à tout groupe fini G, on est capable d'associer une suite de groupes simples
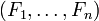 .
.
- Ainsi, à tout groupe fini G, on est capable d'associer une suite de groupes simples
-
Cette suite ne caractérise pas le groupe G (ce qui est dommage, sinon on aurait complètement ramené l'étude des groupes finis et de leur classification à celle des groupes simples !). Prenons pour s'en convaincre le cas du groupe cyclique à 4 éléments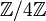 et du groupe de Klein (isomorphe à
et du groupe de Klein (isomorphe à 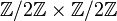 ). Ces deux groupes ont la même suite de facteurs de décomposition
). Ces deux groupes ont la même suite de facteurs de décomposition 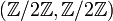 sans pour autant être isomorphes.
sans pour autant être isomorphes.
Elle a cependant une très forte influence sur sa structure. Citons par exemple l'étude des groupes résolubles (c’est-à-dire, dans le cas fini, des groupes dont les facteurs de décomposition sont des groupes cycliques d'ordre premier).
On arrive tout naturellement à une question capitale en théorie des groupes finis, connue sous le nom du problème de l'extension qui s'énonce par:Étant donné deux groupes finis H et K, quels sont les groupes finis G tels que
-
-
-
- H est isomorphe à un sous-groupe distingué de G (que l'on note abusivement toujours H).
-
-
-
-
-
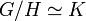 .
.
-
-
Les groupes G solutions de ce problème sont appelés des extensions de H par K .
Les produits directs et semi-directs sont des exemples de solutions au problème de l'extension. Cependant, toute solution du problème de l'extension ne se présente malheureusement pas sous la forme d'un produit direct ou d'un produit semi-direct. On peut le voir par exemple avec le groupe des quaternions, qui est une extension de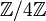 par
par 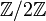 sans pour autant être un produit direct ou un produit semi-direct.
sans pour autant être un produit direct ou un produit semi-direct.Supposons un instant que l'on sache résoudre le problème de l'extension en général. On serait alors capable de reconstruire tous les groupes finis à partir des groupes simples (en résolvant le problème de l'extension de proche en proche à partir d'une suite de groupes simples - qui deviendrait ensuite la suite de facteurs de décomposition du groupe construit).
Le problème de l'extension apparaît donc comme une sorte de réciproque à celui d'associer à un groupe fini une suite de facteurs de décomposition.
-
-
- Cette approche montre que l'étude des groupes finis revient à :
-
-
-
-
-
-
- L'étude des groupes simples.
-
-
-
-
-
-
-
-
-
- Le problème de l'extension.
-
-
-
-
Ainsi les groupes finis simples apparaissent comme les briques élémentaires de la théorie des groupes finis (on peut faire l'analogie avec les nombres premiers en théorie des entiers ! Attention tout de même, la suite des facteurs premiers d'un nombre entier caractérise complètement ce nombre, ce qui n'est pas le cas des groupes simples pour les groupes finis comme on vient de le voir !)
En 1981, après plus d'un demi-siècle de travail acharné et quelques milliers de pages de démonstration, la communauté mathématique donne une classification des groupes finis simples. Plus précisément, tout groupe fini simple appartient à l'une des familles suivantes:-
-
-
- les groupes cycliques dont l'ordre est un nombre premier.
-
-
-
-
-
- les groupes de Chevalley.
-
-
-
-
-
- les groupes alternés
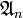 , avec
, avec 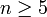 .
.
- les groupes alternés
-
-
-
-
-
- les groupes sporadiques, au nombre de 26.
-
-
Bibliographie
H. Kurzweil et B. Stellmacher, The Theory of Finite Groups. An Introduction. Springer, 2004.
Voir aussi
- Liste des groupes finis simples
- Groupe (mathématiques)
- Permutation pour une approche plus concrète
- Portail des mathématiques
Catégorie : Groupe fini -
Wikimedia Foundation. 2010.