Representation irreductible

Representation irreductible

Représentation irréductible

En mathématiques, une représentation irréductible est un concept utilisé dans le cadre de la théorie des représentation d'un groupe.

Une représentation irréductible est une représentation qui n'admet qu'elle-même et la représentation nulle comme sous-représentation.

Cette notion est importante car le théorème de Maschke démontre que, dans de nombreux cas, une représentation est somme directe de représentations irréductibles.

Sommaire

Définitions et exemples

Définitions

Dans toute la suite de l'article, G désigne un groupe et (V, ρ) une représentation linéaire de G sur un corps K.

  • Une représentation (V, ρ) est dite irréductible si et seulement si les seuls sous-espaces stables sont V et le vecteur nul.
  • Un caractère d'une représentation est dit irréductible si et seulement si la représentation associée l'est.

La théorie des représentations s'exprime aussi en termes de G module. V dispose naturellement d'une structure de G module, dans ce contexte, la définition prend la forme suivante :

  • Une représentation (V, ρ) est dite irréductible si et seulement si V est simple en tant que G module.
  • Une représentation (V, ρ) est dite isotypique si et seulement si les seuls sous-espaces irréductibles stables différents de la représentation nulle sont isomorphes deux à deux.

Exemples

Toutes représentations de dimension un est irréductible.

Il n'existe qu'une représentation irréductible et fidèle du Groupe symétrique d'indice trois. Les articles Représentations du groupe symétrique d'indice trois et Représentations du groupe symétrique d'indice quatre contiennent une analyse exhaustive des représentations irréductibles de ces groupes.

Si V désigne un espace vectoriel réel de dimension deux et G le groupe des isométries linéaires de V, alors l'identité de G est une représentation irréductible.

Théorème de Maschke

Article détaillé : Théorème de Maschke.

Le théorème de Maschke indique que tout sous-espace irréductible de la représentation (V, ρ) est facteur direct, c'est-à-dire qu'il possède un sous-espace supplémentaire stable.

Ce théorème s'applique au moins dans deux cas importants :

Dans ce cas, V dispose d'une structure de module semi-simple. Toute représentation de degré fini de G est alors somme directe de représentations irréductible.

Les démonstrations sont données dans l'article associé.

Cas d'un groupe fini

On suppose dans ce paragraphe de G est un groupe fini g et que la caractéristique de K est soit nulle soit première avec l'ordre du groupe. Le théorème de Maschke s'applique alors. (W, σ) désigne ici une représentation irréductible de G de degré d. On suppose enfin que le polynôme Xg - 1 est scindé dans K.

Caractère

Article détaillé : Caractère d'une représentation d'un groupe fini.

Les caractères des représentations disposent, dans ce contexte, d'un produit hermitien canonique, il fournit une condition nécessaire et suffisante commode pour déterminer l'irréductibilité d'une représentation.

  • Un caractère est irréductible si et seulement si sa norme par le produit hermitien canonique est égal à un.

La démonstration est donnée dans l'article associé.

Représentation régulière

Article détaillé : Représentation régulière.

Soit (V, ρ) la représentation régulière de G. Elle contient toutes les représentations irréductibles de G à un isomorphisme près, plus précisément :

  • Il existe exactement d sous-espaces invariants Wi de V, d'intersection nulle deux à deux, tel que la restriction de ρ, la représentation régulière, à Wi soit isomorphe à (W, σ).

Cette décomposition n'est pas unique. Le nombre de sous-espaces isomorphes à W de V est en général supérieur à d, mais il ne sont pas en somme directe. Il existe néanmoins une unique décomposition de la représentation régulière.

  • Il existe un unique sous-espace maximal SW de V contentant tous les sous-espaces isomorphe à W. Il est appelé composante isotypique de W dans V.

Cette décomposition en composantes isotypiques est unique pour toute représentation de G, elle est appelée décomposition canonique.

Les démonstrations sont données dans l'article associé.

Fonction centrale

Article détaillé : Fonction centrale d'un groupe fini.

La notion de fonction centrale, c'est-à-dire de fonction du groupe G constante sur chaque classe de conjugaison permet de déterminer exactement le nombre de représentations irréductibles :

  • Il existe autant de représentations irréductibles distinctes que de classes de conjugaison dans le groupe.

La démonstration est donnée dans l'article associé.

Algèbre du groupe

Article détaillé : Algèbre d'un groupe fini.

L'algèbre K[G] correspond à un enrichissement de la structure algèbrique de la représentation régulière. Le centre de l'algèbre est un anneau commutatif, sur lequel il est possible d'utiliser des théorèmes d'arithmétique. Ils permettent, par exemple de démontrer les propriétés suivantes :

  • Le degré d'une représentation irréductible divise l'ordre du groupe.

La démonstration est donnée dans l'article associé.

Produit tensoriel

Article détaillé : Produit tensoriel et représentations de groupes finis.

Le produit tensoriel introduit une bijection entre les représentations de deux groupes G1 et G2 et le produit direct G de G1 et G2 :

  • Si (W, σ) est une représentation irréductible de G, le groupe produit direct de G1 et G2, alors il existe une représentation irréductible (W1, σ1) de G1 et une (W2, σ2) de G2 tel que (W, σ) est isomorphe au produit tensoriel des deux représentations précédentes. Réciproquement, tout produit tensoriel de deux représentations irréductibles de G1 et G2 est une représentation irréductible de G.

La démonstration est donnée dans l'article associé.

Représentation induite

Article détaillé : Représentation induite d'un groupe fini.

Dans le cas où N est un sous-groupe normal normal de G, les représentations induites permettent d'établir une relation entre (W, σ) et la restriction de σ à N :

  • Soit il existe un sous-groupe H de G contenant N et différent G tel que (W, σ) est la représentation induite par une représentation irréductible (W1, θ), soit la restriction de σ à N est isotypique.

On en déduit le corollaire suivant :

Il est de plus à noter que le critère d'irréductibilité de Mackey fournit une condition nécessaire et suffisante pour une représentation induite soit irréductible.


Démonstrations
  • Soit il existe un sous-groupe H de G contenant N et différent G tel que (W, σ) est la représentation induite par une représentation irréductible (W1, θ), soit la restriction de σ à N est isotypique.


Soit Wi, où i varie de 1 à n, la décomposition canonique de la restriction de σ à N en composantes isotypiques. On dispose alors de l'égalité :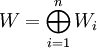

W=\bigoplus_{i=1}^n W_i

Si s est un élément de G et si i est un entier compris entre 1 et n, alors σ(s)Wi est encore une composante isotypique. On remarque que, comme W est une représentation irréductible de G l'action du groupe σ(G) est transitive sur la famille des Wi.

Si n est égal à 1, c'est-à-dire que W1 est égal à W, alors la restriction de σ à N est une représentation isotypique.

Dans le cas contraire, considérons le sous-groupe H de G formé des éléments laissant globalement invariant W1. Soit θ' la restriction de σ à H et θ la représentation de H sur l'espace W1 égal à θ' sur W1. Alors (W, σ) est la représentation induite par une représentation irréductible (W1, θ).

Pour démontrer la proposition suivante, un lemme est nécessaire :

  • Si C est le centre du groupe G, alors le degré d d'une représentation irréductible divise l'ordre du groupe quotient G/C.

Notons c l'ordre du sous-groupe C de G, et (W, σ) une représentation irréductible de G. Si z est un élément de G, alors σ(z) commute avec tous les éléments σ(s) si s parcourt G. Le lemme de Schur permet de conclure que σ(z) est une homothétie, notons λ(z) son rapport. On remarque que l'application λ est un morphisme de groupe de C dans K*.

Considérons alors un entier strictement positif m et la représentation σm produit tensoriel m fois de la représentation σ à valeur dans W 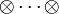\otimes \cdots \otimes W. Si z1, ..., zm est un élément de Cm, alors l'image de z1 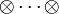\otimes \cdots \otimes zm par σm est une homothétie de rapport λ(z1 ... zm).

Notons H le sous-groupe de Gm formé des éléments (z1 , ..., zm) tel que le produit de toutes les coordonnées soit égal à un. C'est un sous-groupe du centre de Gm, il est donc normal. Par passage au quotient, on obtient une représentation irréductible de Gm/H. Le degré d m de la représentation σm est donc un diviseur de gm/cm-1. Cette relation est vraie pour tout m, ce qui démontre le lemme.

  • Si N est un sous-groupe normal abélien de G, alors le degré d'une représentation irréductible divise l'ordre du groupe quotient G/N.

Démontrons cette proposition par récurrence. La représentation irréductible de G est ici notée (W, σ).

Si la restriction de σ à N est isotypique, alors, comme N est abélien et que les seules représentation irréductibles d'un groupe abélien fini sont de degré un, l'image de N par σ est composée d'homothéties. Notons G' et N' les images de G et N par σ. Considérons la représentation identité de G' à valeur dans GL(W). Le lemme précédent montre que le degré de cette représentation divise l'ordre du groupe quotient de G' par son centre. Or son centre contient N' car ce sous-groupe est composé d'homothéties. Le degré de σ, c'est-à-dire la dimension de W est donc un diviseur de l'ordre de G' /N' . Enfin l'application canonique de G/N dans G' /N' est surjective donc l'ordre de G' /N' est un diviseur de celui de G/N, ce qui termine la démonstration dans ce cas.

Si la restriction de σ à N n'est pas isotypique, alors il existe un groupe H distinct de G et contenant N, tel que la représentation (W, σ) soit induite par une représentation irréductible (W1, θ) de H. Alors le degré de la représentation θ divise l'indice [H:N] par hypothèse de récurrence. Le degré de σ est égal à celui de θ que multiplie l'indice [G:H] et donc est un diviseur de [G:H].[H:N] et donc de [G:N].

Notes et références

Articles sur les Représentations d'un groupe d'ordre fini
Représentations d'un groupe fini | Théorie des représentations | Théorème de Maschke | Caractère | Lemme de Schur | Représentation régulière | Fonction centrale | Produit tensoriel | Algèbre d'un groupe fini | Représentation induite | Réciprocité de Frobenius | Critère d'irréductibilité de Mackey | Groupe symétrique d'indice trois | Groupe symétrique d'indice quatre | Groupe des quaternions | Théorème de Burnside (groupe résoluble) | Théorème de Burnside (problème de 1902)

Liens externes

Références

  • Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]
  • (en) Marshall Hall, The theory of groups [détail des éditions]
  • Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
  • N. Bourbaki Algèbre, Chapitre VIII Paris, Hermann 1958
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Repr%C3%A9sentation irr%C3%A9ductible ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Representation irreductible de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Représentation irréductible — En mathématiques, une représentation irréductible est un concept utilisé dans le cadre de la théorie des représentation d un groupe. C est une représentation qui n admet qu elle même et la représentation nulle comme sous représentation. Le… …   Wikipédia en Français

  • Representation reguliere — Représentation régulière En mathématiques et plus précisément en théorie des groupes, la représentation régulière est une représentation d un groupe fini. Soient G un groupe fini d ordre g, K un corps, V un K espace vectoriel de dimension g et… …   Wikipédia en Français

  • Representation induite d'un groupe fini — Représentation induite d un groupe fini En mathématiques une représentation induite est une méthode de construction d une représentation d un groupe. Cet article traite le cas des groupes finis. Une représentation induite permet de construire à l …   Wikipédia en Français

  • Representation des groupes — Représentation de groupe L idée générale de la théorie des représentations est d essayer d étudier un groupe G en le faisant agir sur un espace vectoriel V de manière linéaire : on essaie ainsi de voir G comme un groupe de matrices (d où le… …   Wikipédia en Français

  • Représentation des groupes — Représentation de groupe L idée générale de la théorie des représentations est d essayer d étudier un groupe G en le faisant agir sur un espace vectoriel V de manière linéaire : on essaie ainsi de voir G comme un groupe de matrices (d où le… …   Wikipédia en Français

  • Représentation linéaire — Représentation de groupe L idée générale de la théorie des représentations est d essayer d étudier un groupe G en le faisant agir sur un espace vectoriel V de manière linéaire : on essaie ainsi de voir G comme un groupe de matrices (d où le… …   Wikipédia en Français

  • Representation d'un groupe de Lie — Représentation d un groupe de Lie En géométrie différentielle, la représentation des groupes de Lie est une approche de l étude des groupes de Lie par représentation comme groupe d endomorphismes linéaires sur un espace vectoriel (voire comme… …   Wikipédia en Français

  • Représentation d'un groupe de lie — En géométrie différentielle, la représentation des groupes de Lie est une approche de l étude des groupes de Lie par représentation comme groupe d endomorphismes linéaires sur un espace vectoriel (voire comme groupe classique). Pour un groupe de… …   Wikipédia en Français

  • Représentation des groupes de Lie — Représentation d un groupe de Lie En géométrie différentielle, la représentation des groupes de Lie est une approche de l étude des groupes de Lie par représentation comme groupe d endomorphismes linéaires sur un espace vectoriel (voire comme… …   Wikipédia en Français

  • Représentation d'algèbre de Lie — En mathématiques, une représentation d une algèbre de Lie est une façon d écrire cette algèbre comme une algèbre de matrices, ou plus généralement d endomorphismes d un espace vectoriel, avec le crochet de Lie donné par le commutateur. Sommaire 1 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”