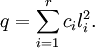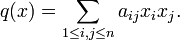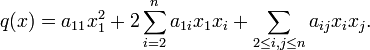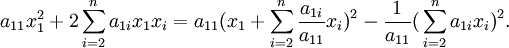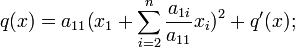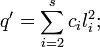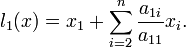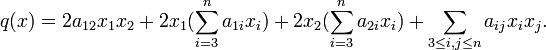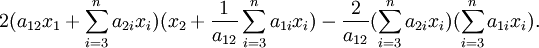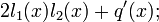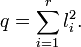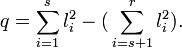- Reduction de Gauss
-
Réduction de Gauss
En mathématiques, la réduction de Gauss est un algorithme permettant de représenter toute forme quadratique sur un espace vectoriel de dimension finie (sur un corps commutatif de caractéristique différente de deux) comme une combinaison linéaire de carrés de formes linéaires indépendantes. La méthode employée est proche de la mise sous forme canonique d'une équation du second degré. Cet algorithme est nommé ainsi en l'honneur du mathématicien Carl Friedrich Gauss.
Sommaire
Enoncé
Réduction de Gauss — Pour toute forme quadratique sur un espace vectoriel de dimension finie, il existe un entier naturel non nul r, des formes linéaires
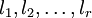 indépendantes et des éléments
indépendantes et des éléments 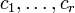 du corps de base, tous non nuls, tels queDémonstration
du corps de base, tous non nuls, tels queDémonstrationOn procède par récurrence sur la dimension.
Dans une base
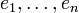 , une forme linéaire s'écrit
, une forme linéaire s'écritEn dimension 1, on a tout simplement
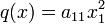 , et il n'y a rien à montrer.
, et il n'y a rien à montrer.Supposons donc la dimension supérieure à 1. On distingue deux cas.
1) L'un des coefficients aii est non nul.
On peut, quitte à permuter les vecteurs de base, supposer que
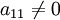 . On écrit séparément les termes où x1 intervient :
. On écrit séparément les termes où x1 intervient :On applique à ces derniers la technique de résolution d'une équation du second degré :
On obtient ainsi que
où
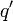 est un polynôme homogène de degré deux par rapport à
est un polynôme homogène de degré deux par rapport à 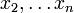 , autrement dit une forme quadratique sur l'espace vectoriel engendré par
, autrement dit une forme quadratique sur l'espace vectoriel engendré par 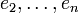 . L'hypothèse de récurrence nous dit que
. L'hypothèse de récurrence nous dit queoù les li sont des combinaisons linéaires de
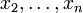 , d'où le résultat avec c1 = a11 et
, d'où le résultat avec c1 = a11 et2) Tous les aii sont nuls et q non nulle.
Il existe des entiers i,j tels que
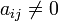 . Comme dans le premier cas, on peut supposer qu'il s'agit de a12. On écrit
. Comme dans le premier cas, on peut supposer qu'il s'agit de a12. On écritLa somme des termes en x1 ou x2 s'écrit aussi
On voit que
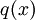 est de la forme
est de la formeoù
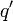 ne dépend que de
ne dépend que de 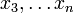 . On conclut en appliquant l'hypothèse de récurrence à
. On conclut en appliquant l'hypothèse de récurrence à 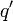 , et en remarquant que 4l1l2 = (l1 + l2)2 − (l1 − l2)2.
, et en remarquant que 4l1l2 = (l1 + l2)2 − (l1 − l2)2.En langage matriciel, cela signifie que toute matrice symétrique est congruente à une matrice diagonale, c'est à dire que pour toute matrice symétrique M d'ordre n, il existe une matrice inversible Q telle que tQMQ soit diagonale (les coefficients diagonaux sont les
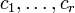 complétés par des zéros si r < n).
complétés par des zéros si r < n).L'entier r est le rang de la forme quadratique. C'est aussi le rang de n'importe quelle matrice représentant cette forme dans une base.
Contrairement aux valeurs propres, les ci ne sont pas uniques, même à permutation près.
Exemples
- Soit
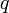 une forme quadratique sur l'espace vectoriel
une forme quadratique sur l'espace vectoriel 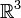 définie par
définie par
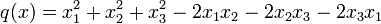
(On a désigné par
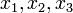 un élément
un élément  de
de 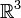 )
)
Alors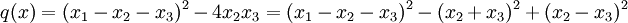 .
.- Autre exemple :
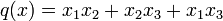
On a alors
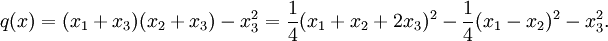
Applications
Si le corps de base est
 le corps des nombres complexes ou plus généralement un corps algébriquement clos, il existe r formes linéaires indépendantes
le corps des nombres complexes ou plus généralement un corps algébriquement clos, il existe r formes linéaires indépendantes 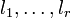 telles que
telles queAutrement dit, sous l'action du groupe linéaire, les formes quadratiques sont classées par leur rang. En langage matriciel, deux matrices symétriques complexes sont congruentes si et seulement si elles sont même rang.
Si le corps de base est
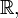 le corps des nombres réels, il faut prendre en compte le signe des ci. Il existe un entier s (inférieur ou égal à r) tel que
le corps des nombres réels, il faut prendre en compte le signe des ci. Il existe un entier s (inférieur ou égal à r) tel queCet entier ne dépend pas de la décomposition d'après la loi d'inertie de Sylvester.
- Si s < = n et r = s, la forme quadratique est positive (définie positive si et seulement si r=n),
- si r < = n et s = 0 elle est négative (définie négative si et seulement si r=n).
Si le corps de base est
 le corps des nombres rationnels ou
le corps des nombres rationnels ou 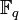 un corps fini, la réduction de Gauss ne permet pas d'effectuer complètement la classification des formes quadratiques.
un corps fini, la réduction de Gauss ne permet pas d'effectuer complètement la classification des formes quadratiques.Elle donne un algorithme pour trouver une base dans laquelle la matrice de q est diagonale.
Liens internes
- Portail des mathématiques
Catégorie : Algèbre bilinéaire
Wikimedia Foundation. 2010.