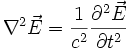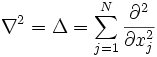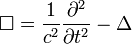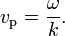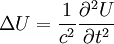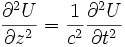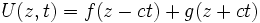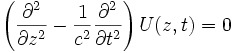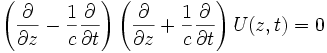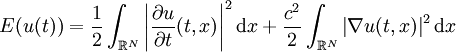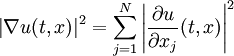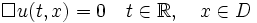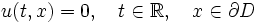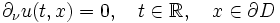Equation d'onde

Équation d'onde

L'équation d'onde est l'équation générale qui décrit la propagation d'une onde, qui peut être représentée par une grandeur scalaire ou vectorielle.

Dans le cas vectoriel, en espace libre, dans un milieu homogène, linéaire et isotrope, l'équation d'onde s'écrit :

$\nabla ^2 \vec E=\frac {1}{c^2}\frac {\partial ^2\vec E}{\partial t^2}$

L'opérateur

$\nabla^2=\Delta=\sum_{j=1}^{N} \frac{\partial^2}{\partial x_j^2}$

(où N est la dimension de l'espace) est appelé laplacien et on note parfois

$\square=\frac{1}{c^2}\frac{\partial^2}{\partial t^2}-\Delta$

l'opérateur d'onde, ou d'alembertien.

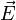$\vec E$ décrit à la fois l'amplitude de l'onde, et sa polarisation (par son caractère vectoriel). c est assimilable à la vitesse de propagation de l'onde, comme nous le verrons plus bas. {c} pour sa part est une constante fixe égale à la vitesse de la propagation de l'onde, par exemple la vitesse du son qui est de 343m/s dans l'air à 20 °C. Dans le cas de phénomènes plus complexes tels la propagation de l'onde variant avec sa fréquence (soit la dispersion), on remplace {c} par la vélocité de phase:

$v_\mathrm{p} = \frac{\omega}{k}.$

En s'intéressant à chacune des composantes de 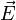$\vec E$ (en projetant la relation dans chacune des directions de l'espace), nous obtenons une équation portant sur un scalaire, appelée équation de d'Alembert :

$\Delta U=\frac {1}{c^2}\frac {\partial^2 U}{\partial t^2}$

Sommaire

1 L'équation en dimension 1 d'espace
2 Équation d'onde en dimension supérieure
3 Conservation de l'énergie
4 Équation dans un domaine borné avec condition au bord

L'équation en dimension 1 d'espace

En dimension 1 d'espace, l'équation s'écrit

$\frac {\partial ^2 U}{\partial z^2}=\frac {1}{c^2}\frac {\partial ^2 U}{\partial t^2}$

Lorsque la variable z parcourt toute la droite réelle, la solution générale de cette équation est la somme de deux fonctions :

$U(z,t)=f(z-ct)+g(z+ct)\!$

En effet, on peut écrire :

$\left(\frac {\partial ^2}{\partial z^2}-\frac {1}{c^2}\frac {\partial ^2}{\partial t^2}\right) U(z,t) = 0$

soit :

$\left(\frac {\partial}{\partial z}-\frac {1}{c}\frac {\partial}{\partial t}\right)\left(\frac {\partial}{\partial z}+\frac {1}{c}\frac {\partial}{\partial t}\right) U(z,t) = 0$

Et si l'on pose a=z-ct et b=z+ct, on obtient :

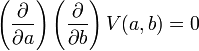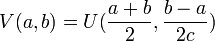
$\left(\frac {\partial}{\partial a}\right)\left(\frac {\partial}{\partial b}\right) V(a,b) = 0$ où $V(a,b)= U(\frac{a+b}{2},\frac{b-a}{2c})$

Qui se résout en : $V (a, b) = f (a) + g (b)$ soit $U (z, t) = f (z - c t) + g (z + c t)$

Le premier terme est une onde se propageant dans le sens des z croissants (appelée onde progressive), et le deuxième terme dans le sens des z décroissants (appelée onde régressive).

Exemple : Onde sur une corde vibrante

Équation d'onde en dimension supérieure

Conservation de l'énergie

Si $u$ est une solution de l'équation des ondes alors l'énergie

$E(u(t))=\frac{1}{2}\int_{\mathbb{R}^N} \left|\frac{\partial u}{\partial t}(t,x)\right|^2\mathrm{d}x+\frac{c^2}{2}\int_{\mathbb{R}^N} \left|\nabla u(t,x)\right|^2\mathrm{d}x$

est conservée au cours du temps. Ici on a noté $N$ la dimension d'espace et

$\left|\nabla u(t,x)\right|^2=\sum_{j=1}^{N} \left|\frac{\partial u}{\partial x_j}(t,x)\right|^2$

Équation dans un domaine borné avec condition au bord

On peut également considérer l'équation des ondes dans un domaine de l'espace D:

$\square u(t,x) =0\quad t\in\mathbb{R},\quad x\in D$

avec des conditions aux limites, par exemple:

$u(t,x)=0,\quad t\in \mathbb{R},\quad x \in \partial D$

(conditions aux limites de Dirichlet) où 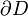$\partial D$ est le bord du domaine $D$ , ou

$\partial_{\nu} u(t,x)=0,\quad t\in\mathbb{R},\quad x\in \partial D$

(conditions aux limites de Neumann) où 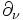$\partial_{\nu}$ est la dérivée normale extérieure au bord $\partial D$

Ce document provient de « %C3%89quation d%27onde ».

Catégories : Mécanique ondulatoire | Équation aux dérivées partielles

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Equation d'onde de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Équation d'onde — L équation d onde est l équation générale qui décrit la propagation d une onde, qui peut être représentée par une grandeur scalaire ou vectorielle. Dans le cas vectoriel, en espace libre, dans un milieu homogène, linéaire et isotrope, l équation… … Wikipédia en Français
équation d’onde — banginė lygtis statusas T sritis fizika atitikmenys: angl. wave equation vok. Wellengleichung, f rus. волновое уравнение, n pranc. équation de l’onde, f; équation d’onde, f … Fizikos terminų žodynas
équation d’onde — bangos lygtis statusas T sritis fizika atitikmenys: angl. wave equation vok. Wellengleichung, f rus. уравнение волны, n pranc. équation d’onde, f … Fizikos terminų žodynas
Equation aux derivees partielles — Équation aux dérivées partielles En mathématiques, plus précisément en calcul différentiel, une équation aux dérivées partielles ou équation différentielle partielle (EDP) est une équation dont les solutions sont les fonctions inconnues vérifiant … Wikipédia en Français
Equation de Schrodinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Equation de schrodinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Équation de Schrodinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Équation de Shroedinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Équation de schrodinger — Équation de Schrödinger Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français
Équation de schrödinger — Cet article fait partie de la série Mécanique quantique Postulats de la mécanique quantique Histoire … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Equation d'onde

Équation d'onde

Sommaire

L'équation en dimension 1 d'espace

Équation d'onde en dimension supérieure

Conservation de l'énergie

Équation dans un domaine borné avec condition au bord

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Equation d'onde

Équation d'onde

Sommaire

L'équation en dimension 1 d'espace

Équation d'onde en dimension supérieure

Conservation de l'énergie

Équation dans un domaine borné avec condition au bord

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link