- Decomposition de Dunford
-
Décomposition de Dunford
En mathématiques, la décomposition de Dunford s'inscrit dans la problématique de la réduction d'endomorphisme. Cette approche consiste à décomposer l'espace vectoriel en une somme directe de sous-espaces stables où l'expression de l'endomorphisme est plus simple.
Ce n'est pas une réduction dans le sens où elle n'est pas maximale. C'est-à-dire qu'il est parfois possible de pousser la décomposition en sous-espaces vectoriels plus petits.
Elle suppose comme hypothèses que l'espace vectoriel est de dimension finie et que le polynôme minimal est scindé, c'est-à-dire qu'il s'exprime comme produit de polynômes du premier degré. C'est toujours le cas si le corps est algébriquement clos, comme par exemple celui des nombres complexes. Dans le cas ou la propriété n'est pas vérifiée, alors il est possible d'étendre le corps à sa clôture algébrique, et l'espace vectoriel à ce nouveau corps et dans ce contexte d'appliquer la décomposition de Dunford. Le corps des nombres réels se voit par exemple très généralement étendre pour permettre une application de cette décomposition.
La décomposition de Dunford prouve que tout endomorphisme est la somme d'un endomorphisme diagonalisable et d'un endomorphisme nilpotent, les deux endomorphismes commutant et étant uniques.
Cette décomposition est largement appliquée. Elle permet un calcul matriciel souvent rapide. C'est néanmoins souvent sous la forme de la réduction de Jordan qu'elle est utilisée.
Sommaire
Théorème
Le théorème de diagonalisabilité permet de déterminer la structure de u quand il admet un polynôme annulateur scindé à racines simples. La décomposition de Dunford s'applique à un cas plus général.
Théorème de la décomposition de Dunford — Soit u un endomorphisme d'un espace vectoriel E. Si u admet un polynôme minimal scindé, alors il peut s'écrire sous la forme u=d+n avec d un endomorphisme diagonalisable et n un endomorphisme nilpotent tels que d et n commutent (c'est-à-dire dn=nd). De plus d et n sont des polynômes en u et sont uniques.
Démonstration
Via les sous-espaces caractéristiques
Article détaillé : Sous-espace caractéristique.L'idée initiale de cette approche est donnée par la proposition suivante, démontrée dans l'article sur les polynômes d'endomorphismes dans le paragraphe sur les polynômes minimaux :
-
- Soit
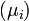 une décomposition en facteurs de degré supérieur ou égal à 1 et premiers entre eux du polynôme minimal
une décomposition en facteurs de degré supérieur ou égal à 1 et premiers entre eux du polynôme minimal 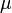 d'un endomorphisme u. Alors la suite des noyaux
d'un endomorphisme u. Alors la suite des noyaux 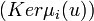 est une décomposition de l'espace E en somme directe de sous-espaces stables par l'endomorphisme.
est une décomposition de l'espace E en somme directe de sous-espaces stables par l'endomorphisme.
- Soit
Or, si le polynôme minimal est scindé, il peut s'écrire sous la forme:
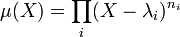
Si l'on note
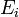 le noyau de l'endomorphisme
le noyau de l'endomorphisme 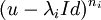 , alors le paragraphe précédent nous indique que la suite
, alors le paragraphe précédent nous indique que la suite 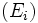 forme une somme directe de l'espace E de sous-espaces non réduits à 0 et stables par l'endomorphisme. On appelle ces sous-espaces les sous-espaces caractéristiques. Nous avons alors les trois propriétés suivantes:
forme une somme directe de l'espace E de sous-espaces non réduits à 0 et stables par l'endomorphisme. On appelle ces sous-espaces les sous-espaces caractéristiques. Nous avons alors les trois propriétés suivantes:-
- L'espace E est somme directe de ces sous-espaces caractéristiques.
- Les sous-espaces caractéristiques sont non réduits au vecteur nul et stable par l'endomorphisme. La restriction de l'endomorphisme à
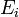 est la somme d'une homothétie de rapport
est la somme d'une homothétie de rapport 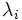 et d'un endomorphisme nilpotent d'ordre
et d'un endomorphisme nilpotent d'ordre 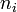 .
. - La suite des
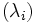 est la suite des valeurs propres (i.e. le spectre de u). Les sous-espaces propres associés sont inclus dans les sous-espaces caractéristiques.
est la suite des valeurs propres (i.e. le spectre de u). Les sous-espaces propres associés sont inclus dans les sous-espaces caractéristiques.
Ces considérations permettent de démontrer la décomposition de Dunford. Elle permettent de plus de démontrer les propriétés suivantes :
-
- Le polynôme minimal est le produit des polynômes de degré 1 et de racine les valeurs propres à la puissance l'indice de l'endomorphisme nilpotent associé.
-
- Le polynôme caractéristique est le produit des polynômes de degré 1 et de racine les valeurs propres à la puissance la dimension de l'espace caractéristique associé.
-
- Le déterminant est égal au produit des valeurs propres élevées à la puissance la dimension de l'espace caractéristique associé.
-
- La trace est égale à la somme des valeurs propres pondérées par les dimensions des espaces caractéristiques associés.
Démonstration-
- L'espace E est somme directe de ces sous-espaces caractéristiques.
Le polynôme minimal est scindé, donc il s'écrit sous la forme de produits des éléments de la suite
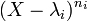 . La proposition précédente nous indique que la suite
. La proposition précédente nous indique que la suite 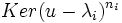 forme une somme directe de sous-espaces stables. Par définitions des sous-espaces caractéristiques, nous venons de démontrer la proposition.
forme une somme directe de sous-espaces stables. Par définitions des sous-espaces caractéristiques, nous venons de démontrer la proposition.-
- Les sous-espaces caractéristiques sont non réduits au vecteur nul et stable par l'endomorphisme. La restriction de l'endomorphisme à
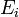 est la somme d'une homothétie de rapport
est la somme d'une homothétie de rapport 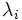 et d'un endomorphisme nilpotent d'ordre
et d'un endomorphisme nilpotent d'ordre 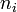 .
.
- Les sous-espaces caractéristiques sont non réduits au vecteur nul et stable par l'endomorphisme. La restriction de l'endomorphisme à
Considérons le polynôme
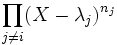 . Ce polynôme n'est pas minimal. Donc la somme directe
. Ce polynôme n'est pas minimal. Donc la somme directe 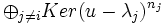 n'est pas l'espace entier. Cela démontre de
n'est pas l'espace entier. Cela démontre de 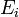 n'est pas réduit au vecteur nul.
n'est pas réduit au vecteur nul.La restriction de u à
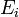 s'écrit
s'écrit 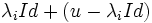 le premier terme est bien une homothétie, la définition du sous-espace caractéristique nous garantit que le deuxième terme est nilpotent.
le premier terme est bien une homothétie, la définition du sous-espace caractéristique nous garantit que le deuxième terme est nilpotent.-
- La suite des
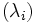 est la suite des valeurs propres. Les sous-espaces propres associés sont inclus dans les sous-espaces caractéristiques.
est la suite des valeurs propres. Les sous-espaces propres associés sont inclus dans les sous-espaces caractéristiques.
- La suite des
Montrons que
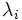 est une valeur propre. Considérons le noyau de l'endomorphisme nilpotent de la dernière proposition. Par construction d'un endomorphisme nilpotent, il n'est pas réduit au vecteur nul. La restriction de u à ce noyau est une homothétie de rapport
est une valeur propre. Considérons le noyau de l'endomorphisme nilpotent de la dernière proposition. Par construction d'un endomorphisme nilpotent, il n'est pas réduit au vecteur nul. La restriction de u à ce noyau est une homothétie de rapport 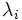 , ce qui démontre qu’elle est valeur propre et que l'espace propre associée est inclus dans l'espace caractéristique.
, ce qui démontre qu’elle est valeur propre et que l'espace propre associée est inclus dans l'espace caractéristique.Considérons alors une valeur propre
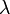 tout vecteur propre associé a pour polynôme minimal
tout vecteur propre associé a pour polynôme minimal 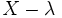 . Or ce polynôme minimal divise
. Or ce polynôme minimal divise 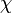 . Nous venons de démontrer que
. Nous venons de démontrer que 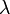 est une racine de
est une racine de 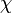 .
.-
- L'endomorphisme u est la somme d'un endomorphisme diagonalisable et d'un endomorphisme nilpotent. Les deux endomorphismes commutent entre eux.
Considérons l'endomorphisme d sur E, qui pour tout vecteur
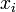 de
de 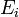 associe
associe 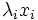 . Comme la somme des
. Comme la somme des 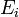 est directe et est égal à E, cet endomorphisme est bien défini et il est diagonalisable.
est directe et est égal à E, cet endomorphisme est bien défini et il est diagonalisable.Considérons l'endomorphisme n sur E, qui pour tout vecteur
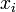 de
de 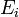 associe
associe 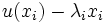 . Comme la somme des
. Comme la somme des 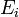 est directe et est égal à E, cet endomorphisme est bien défini et il est nilpotent sur tous les espaces caractéristique,donc il est nilpotent.
est directe et est égal à E, cet endomorphisme est bien défini et il est nilpotent sur tous les espaces caractéristique,donc il est nilpotent.La somme d + n est égal à u et d et n commutent entre eux sur chaque espace caractéristique. La somme des espaces caractéristique est égal à E. L'égalité et la commutativité sont donc vraies sur E.
-
- Le polynôme minimal est le produit des polynômes de degré 1 et de racine les valeurs propres à la puissance l'indice de l'endomorphisme nilpotent associé.
Il suffit de remarquer que
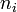 est l'indice de l'endomorphisme nilpotent qu'est la restriction de
est l'indice de l'endomorphisme nilpotent qu'est la restriction de 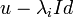 à l'espace caractéristique associé.
à l'espace caractéristique associé.-
- Le polynôme caractéristique est le produit des polynômes de degré 1 et de racine les valeurs propres à la puissance la dimension de l'espace caractéristique associé.
Il suffit de calculer le polynôme caractéristique dans une base de Jordan.
-
- Le déterminant est égal au produit des valeurs propres élevées à la puissance de la dimension de l'espace caractéristique associé.
Il suffit de calculer le déterminant dans une base de Jordan.
-
- La trace est égale à la somme des valeurs propres multipliées par la dimension de l'espace caractéristique associé.
Il suffit de calculer la trace dans une base de Jordan.
Via les projecteurs
Article détaillé : Projecteur (mathématiques).Un résultat notoire de l'approche par les polynômes d'endomorphismes réside dans le fait que la connaissance du polynôme minimal permet de définir une algorithmique fournissant à la fois les projecteurs sur les espaces caractéristiques mais aussi la composante diagonale et nilpotente de l'endomorphisme.
-
- La projection sur Ei parallèlement à la somme directe des autres espaces caractéristiques s'exprime comme un polynôme de l'endomorphisme u.
- La composante diagonale d de l'endomorphisme u s'exprime comme un polynôme de l'endomorphisme u.
- La composante nilpotente n de l'endomorphisme u s'exprime comme un polynôme de l'endomorphisme u.
Démonstration-
- La projection sur Ei parallèlement à la somme directe des autres espaces caractéristiques s'exprime comme un polynôme de l'endomorphisme u.
C'est une conséquence directe de la dernière proposition du paragraphe sur les idéaux annulateurs. En effet, la famille des polynômes
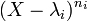 est bien une famille de polynômes premiers deux à deux.
est bien une famille de polynômes premiers deux à deux.-
- La composante diagonale d de l'endomorphisme u s'exprime comme un polynôme de l'endomorphisme u.
L'égalité suivante
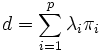 montre que la composante diagonale est bien un polynôme en u.
montre que la composante diagonale est bien un polynôme en u.-
- La composante nilpotente n de l'endomorphisme u s'exprime comme un polynôme de l'endomorphisme u.
L'égalité suivante est vérifiée
![n=u-d=(X-P)[u]\,](/pictures/frwiki/102/f1bddd0eb7de02080311faa6753e39cc.png) , n est donc aussi un polynôme en u.
, n est donc aussi un polynôme en u.Cas d'applications
En dimension finie le théorème de Cayley-Hamilton assure que χu(u) = 0 où χu désigne le polynôme caractéristique de u. Si χu est scindé alors u est décomposable.
C'est en particulier le cas pour tout endomorphisme d'un espace de dimension finie sur un corps algébriquement clos (
 notamment).
notamment).Réduction de Jordan
La décomposition de Dunford permet d'obtenir la réduction de Jordan en dimension finie. En effet, d et n commutent donc les sous-espaces propres de d sont stables par n.
La restriction de n au sous-espace propre admet une matrice formée de blocs de Jordan nilpotents ce qui donne, en ajoutant λIp, des blocs de Jordan pour d+n dans une base adaptée. Ainsi on obtient une matrice diagonale par blocs formée de blocs de Jordan en utilisant l'union de ces bases.
- Portail des mathématiques
Catégorie : Application linéaire -
Wikimedia Foundation. 2010.

