Forme Sesquilinéaire

Forme sesquilinéaire

En algèbre, une forme sesquilinéaire sur un espace vectoriel complexe E est une application de E × E dans $\mathbb C$ , linéaire selon l'une des variables et antilinéaire (aussi dit semi-linéaire) par rapport à l'autre variable. Elle possède donc une propriété de « un-et-demi » linéarité (cf. sesqui). C'est l'équivalent complexe aux formes bilinéaires réelles.

Les formes sesquilinéaires les plus étudiées sont les formes hermitiennes. Parmi celle-ci, les formes hermitiennes définies positives permettent de munir E d'un produit scalaire et ouvrent à l'étude des espaces hermitiens, des espaces préhilbertiens complexes et des espaces de Hilbert.

Définitions et conventions

Les conventions diffèrent quant au choix de l'argument qui est linéaire. Le choix ci-dessus (première variable : linéaire, deuxième variable : antilinéaire) est plus courant en mathématiques (peut-être pas universel), mais le choix opposé est utilisé par tous les physiciens, ceci étant dû à l'origine à l'utilisation de la notation bra-ket.

Forme antilinéaire : Soit E un $\mathbb C$ -espace vectoriel, l'application φ de E dans $\mathbb C$ est antilinéaire si et seulement si :

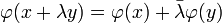
Elle respecte l'addition et presque la multiplication scalaire : pour tous x, y de E, pour tout λ de $\mathbb C$ : $\varphi (x + \lambda y) = \varphi(x) + \bar \lambda \varphi(y)\,$

Forme sesquilinéaire : L'application f de E × E → $\mathbb C$ est une forme sesquilinéaire si et seulement si :

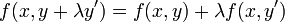
a) Elle est linéaire à droite : pour tout x, y, y' de E, pour tout λ de $\mathbb C$ : $f(x,y+\lambda y') = f(x,y) + \lambda f(x,y')\,$

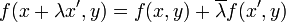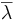b) Elle est antilinéaire à gauche, ce qui signifie que pour tout x, x', y de E, pour tout λ de $\mathbb C$ : $f(x+ \lambda x',y) = f(x,y) + \overline{\lambda} f(x',y)$ où $\overline{\lambda}$ est le conjugué de λ.

Forme hermitienne : c'est une forme sesquilinéaire qui vérifie la propriété de symétrie hermitienne

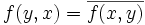
c) Pour tous x et y de E, $f(y,x) = \overline{f(x,y)}$

En particulier : 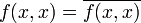$f(x,x) = \overline{f(x,x)}$ , donc

f (x, x)

est un réel.

Forme hermitienne définie positive : c'est une forme hermitienne telle que

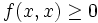
d) Pour tout x de E, $f(x,x) \ge 0$

e) Pour tout x de E, 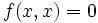$f(x,x) = 0\,$ implique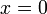 $x = 0\,$

Une forme hermitienne définie positive est encore appelée produit scalaire (sous-entendu au sens complexe).

Exemples

En dimension finie, on prouve que les seules formes sesquilinéaires sont celles définies par

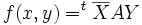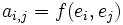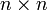$f(x,y) =^t \overline X AY$ où X et Y sont les vecteurs colonnes, coordonnées de x et y dans la base $(e 1,..., e n)$ , et où A est la matrice définie par $a_{i,j} = f(e_i,e_j)\,$ . L'ensemble des formes sesquilinéaires dans un ensemble de dimension n est donc en bijection avec l'ensemble des matrices carrée $n \times n$ .

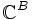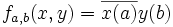Soit B un ensemble non vide et $\mathbb C^B$ le $\mathbb C$ -espace vectoriel des applications de B dans $\mathbb C$ , et soient a et b deux éléments de B. La forme $f a, b$ définie par $f_{a,b}(x,y) =\overline{ x(a)}y(b)$ est une forme sesquilinéaire.

Dans un espace métrique, le produit interne (scalaire) est sesquilinéaire. Pour tout x, y, z de E et pour tout a, u de $\mathbb C$ on a :

(ax+uy|z) = a(x|z) + u(y|z)
(x|ay+uz) = â(x|y) + û(y|z) où â et û sont respectivement les complexes conjugués de a et u.

Articles connexes

Articles de mathématiques en rapport avec l'algèbre bilinéaire

Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz

modifier

Portail des mathématiques

Ce document provient de « Forme sesquilin%C3%A9aire ».

Catégorie : Algèbre bilinéaire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Forme Sesquilinéaire de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Forme sesquilineaire — Forme sesquilinéaire En algèbre, une forme sesquilinéaire sur un espace vectoriel complexe E est une application de E × E dans , linéaire selon l une des variables et antilinéaire (aussi dit semi linéaire) par rapport à l autre variable. Elle… … Wikipédia en Français
Forme sesquilinéaire — En mathématiques, une forme sesquilinéaire entre deux espace vectoriels sur des corps est une fonction de deux variables qui généralise à la fois les formes bilinéaires et les formes sesquilinéaires complexes. Sommaire 1 Généralités 1.1… … Wikipédia en Français
Forme sesquilinéaire antihermitienne — ● Forme sesquilinéaire antihermitienne synonyme de forme bilinéaire antiautoadjointe … Encyclopédie Universelle
Forme sesquilinéaire complexe — Cet article concerne un cadre élémentaire. Pour un cadre général, voir Forme sesquilinéaire et Forme hermitienne. En algèbre, une forme sesquilinéaire sur un espace vectoriel complexe E est une application de E × E dans , linéaire selon l une des … Wikipédia en Français
Forme Bilinéaire — En mathématiques, le concept de forme bilinéaire est une notion algébrique s appliquant à un espace vectoriel. Il correspond à une application qui, à deux vecteurs définis sur le même corps de nombres associe un scalaire. L étude des formes… … Wikipédia en Français
Forme bilineaire — Forme bilinéaire En mathématiques, le concept de forme bilinéaire est une notion algébrique s appliquant à un espace vectoriel. Il correspond à une application qui, à deux vecteurs définis sur le même corps de nombres associe un scalaire. L étude … Wikipédia en Français
Forme Quadratique — En mathématiques, une forme quadratique est un polynôme homogène de degré deux avec un nombre quelconque de variables. Par exemple, la distance comprise entre deux points dans un espace euclidien à trois dimensions s obtient en calculant la… … Wikipédia en Français
Forme hermitienne sur un espace vectoriel E sur le corps des nombres complexes — ● Forme hermitienne sur un espace vectoriel E sur le corps des nombres complexes forme sesquilinéaire telle que, pour tout couple (x,y) de E × E … Encyclopédie Universelle
Forme hermitienne — Cet article concerne le cas général abstrait. Pour un cas plus élémentaire, voir Forme sesquilinéaire complexe. En mathématiques, une forme hermitienne est une fonction de deux variable sur un espace vectoriel sur un corps relativement à une… … Wikipédia en Français
Forme bilinéaire — En mathématiques, plus précisément en algèbre linéaire, une forme bilinéaire est un type particulier d application qui, à deux vecteurs d un même espace vectoriel (sur un certain corps commutatif) associe un scalaire (c est à dire un élément de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Forme Sesquilinéaire