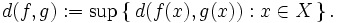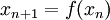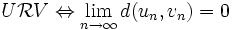- Espace Complet
-
Espace complet
En mathématiques, un espace métrique M est dit complet ou espace complet si toute suite de Cauchy de M a une limite dans M (c’est-à-dire qu'elle converge dans M). La propriété de complétude dépend de la distance. Il est donc important de toujours préciser la distance que l'on prend quand on parle d'espace complet.
Intuitivement, un espace est complet s'il « n'a pas de trou », s'il « n'a aucun point manquant ». Par exemple, les nombres rationnels ne forment pas un espace complet, puisque
 n'y figure pas alors qu'il existe une suite de Cauchy de nombres rationnels ayant cette limite. Il est toujours possible de « remplir les trous » amenant ainsi à la complétion d'un espace donné.
n'y figure pas alors qu'il existe une suite de Cauchy de nombres rationnels ayant cette limite. Il est toujours possible de « remplir les trous » amenant ainsi à la complétion d'un espace donné.La complétude peut aussi être définie pour des espaces uniformes, comme les groupes topologiques.
Sommaire
Exemples
- Soit l'espace
 des nombres rationnels muni de la distance d(x,y) = |x - y|. Cet espace n'est pas complet. En effet, considérons la suite définie par :
des nombres rationnels muni de la distance d(x,y) = |x - y|. Cet espace n'est pas complet. En effet, considérons la suite définie par :
-
- x1 = 1 et
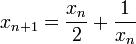 .
.
- x1 = 1 et
- C'est une suite de Cauchy de nombres rationnels mais elle ne converge vers aucune limite appartenant à
 . En fait elle converge vers le nombre irrationnel
. En fait elle converge vers le nombre irrationnel  .
.
- L'intervalle ouvert ]0,1[ muni de la distance d(x,y) = |x - y| n'est pas complet non plus. La suite
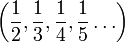 est une suite de Cauchy mais elle n'a pas de limite dans l'intervalle.
est une suite de Cauchy mais elle n'a pas de limite dans l'intervalle.
- L'ensemble ]0,1[ muni de la distance
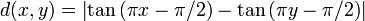 est complet.
est complet.
- L'intervalle réel fermé [0,1] muni de la distance usuelle est complet.
- L'espace
 des nombres réels et l'espace
des nombres réels et l'espace  des nombres complexes munis de la distance usuelle d(x,y) = |x - y|, sont complets ainsi que l'espace euclidien
des nombres complexes munis de la distance usuelle d(x,y) = |x - y|, sont complets ainsi que l'espace euclidien 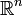 muni de la norme usuelle.
muni de la norme usuelle.
- Les espaces vectoriels normés peuvent être complets ou pas ; ceux qui le sont sont appelés espaces de Banach. Tous les espaces vectoriels normés de dimension finie sur un corps complet sont complets.
- L'espace
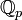 des nombres p-adiques muni de la distance p-adique est complet pour tout nombre premier p. Cet espace complète
des nombres p-adiques muni de la distance p-adique est complet pour tout nombre premier p. Cet espace complète  avec la métrique p-adique tout comme
avec la métrique p-adique tout comme  complète
complète  avec la métrique euclidienne.
avec la métrique euclidienne.
- Si S est un ensemble donné, l'ensemble
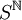 des suites de S devient un espace métrique complet si on définit la distance entre les suites
des suites de S devient un espace métrique complet si on définit la distance entre les suites 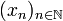 et
et 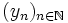 comme étant égale à
comme étant égale à 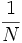 où N est le plus petit indice pour lequel
où N est le plus petit indice pour lequel 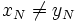 , ou 0 si un tel indice n'existe pas.
, ou 0 si un tel indice n'existe pas.
Quelques théorèmes
- Un espace métrique (E,d) est complet si et seulement si l'intersection de toute suite décroissante de fermés bornés non vides Fn dont la suite des diamètres tend vers 0 a une intersection non vide (théorème des complets emboîtés).
- Tout espace métrique compact est complet. En fait, un espace métrique est compact si et seulement s’il est complet et précompact.
- Un sous-espace d'un espace complet est complet si et seulement s’il est fermé.
- Si X est un ensemble et M un espace métrique complet, alors l'ensemble B(X,M) des fonctions bornées de X dans M est un espace métrique complet. On définit la distance dans B(X,M) en termes de distance dans M :
- Si X est un espace topologique et M un espace métrique complet, alors l'ensemble Cb(X,M) des fonctions continues bornées de X dans M est un sous-espace clos de B(X,M) et donc également complet.
- Le théorème de Baire montre que tout espace métrique complet est un espace de Baire.
- Théorème du point fixe : toute application f contractante d'un espace métrique complet dans lui-même admet un unique point fixe qui est limite de toute suite définie de la manière suivante:
-
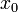 quelconque
quelconque
- Tout produit fini d'espaces métriques complets est complet pour la distance induite.
- Soit
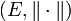 un espace vectoriel normé. Les propriétés suivantes sont équivalentes:
un espace vectoriel normé. Les propriétés suivantes sont équivalentes:
-
- i) E est complet
-
- ii) toute série normalement convergente d'éléments de E est convergente.
Complété d'un espace métrique
Pour tout espace métrique M, il est possible de construire un espace métrique complet M' (également noté
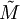 ou
ou 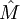 ) qui contient M comme sous-espace dense. Il possède la propriété suivante : si N est un espace métrique complet quelconque et f est une fonction uniformément continue de M vers N, alors il existe une unique fonction uniformément continue f' de M' vers N qui prolonge f. M' est appelée complété de M.
) qui contient M comme sous-espace dense. Il possède la propriété suivante : si N est un espace métrique complet quelconque et f est une fonction uniformément continue de M vers N, alors il existe une unique fonction uniformément continue f' de M' vers N qui prolonge f. M' est appelée complété de M.Le complété de M peut être construit comme l'ensemble des classes d'équivalence des suites de Cauchy de M. Pour deux suites de Cauchy
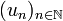 et
et 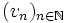 de M, on définit alors la relation :
de M, on définit alors la relation :où d est la distance sur l'ensemble M. Cette relation est bien une relation d'équivalence. On note alors
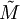 son ensemble quotient.
son ensemble quotient.Il s'agit alors de munir
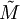 d'une distance qui le rendra complet. Sur l'ensemble des suites de Cauchy, on définit l'application f qui, à deux suites de Cauchy U = (un) et V = (vn), associe le réel
d'une distance qui le rendra complet. Sur l'ensemble des suites de Cauchy, on définit l'application f qui, à deux suites de Cauchy U = (un) et V = (vn), associe le réel 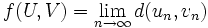 . Cette relation est bien une application car, les suites U et V étant de Cauchy, on peut prouver que la suite (d(un,vn)) est une suite de Cauchy de
. Cette relation est bien une application car, les suites U et V étant de Cauchy, on peut prouver que la suite (d(un,vn)) est une suite de Cauchy de 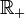 , donc une suite convergente (car
, donc une suite convergente (car 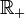 , muni de la distance usuelle, est complet). Cette application vérifie toutes les propriétés d'une distance sauf une : f(U,V) = 0 n'implique pas forcément que U = V.
, muni de la distance usuelle, est complet). Cette application vérifie toutes les propriétés d'une distance sauf une : f(U,V) = 0 n'implique pas forcément que U = V.En revanche, de cette application, on peut induire une application sur l'ensemble quotient
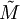 , application qui, aux classes de U et V, notées
, application qui, aux classes de U et V, notées 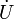 et
et 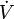 , associe
, associe 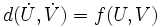 . On démontre que cette définition est indépendante des représentants choisis et définit bien une distance sur
. On démontre que cette définition est indépendante des représentants choisis et définit bien une distance sur 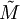 .
.L'espace originel est plongé dans le nouvel espace par identification d'un élément x de M à la classe d'équivalence qui contient la suite constante de valeur x.
On démontre alors que l'espace
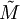 , muni de la distance d, est complet et que M est dense dans
, muni de la distance d, est complet et que M est dense dans 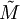 .
.La construction des nombres réels est un cas particulier; l'ensemble des nombres réels est le complété de l'ensemble des nombres rationnels, la valeur absolue usuelle étant utilisée comme distance. En utilisant d'autres notions de distance sur les nombres rationnels, on obtient d'autres ensembles, les nombres p-adiques.
Si cette procédure est appliquée à un espace vectoriel normé, on obtient un espace de Banach contenant l'espace original comme sous-espace dense. Appliquée à un espace préhilbertien, on obtient un espace de Hilbert.
Espace topologiquement complet
La complétude est une propriété métrique, mais pas topologique, ce qui signifie qu'un espace métrique complet peut être homéomorphe à un espace qui ne l'est pas. L'ensemble des nombres réels, par exemple, est complet et homéomorphe à l'intervalle ]0,1[ muni de la topologie induite par la topologie usuelle de
 qui n'est pas complet.
qui n'est pas complet.En topologie, un espace est considéré comme topologiquement complet s'il existe une métrique complète induisant la topologie de cet espace. Un tel espace est également appelé espace polonais.
Un tel espace est un cas particulier d'espace de Baire.
Exemple : c'est le cas de l'ensemble ]0,1[ qui n'est pas complet avec la distance usuelle, mais qui le devient avec la distance d(x,y) = | tan(πx − π / 2) − tan(πy − π / 2) | .
Autre acception du terme
L'épithète "complet" est parfois utilisé dans le sens suivant: un ensemble ordonné est dit complet si toute partie admet une borne supérieure (avec la convention que tout élément majore l'ensemble vide et donc que
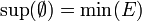 ). Ceci est équivalent (voir ci-dessous) à ce que toute partie possède une borne inférieure (avec la convention opposée pour l'ensemble vide:
). Ceci est équivalent (voir ci-dessous) à ce que toute partie possède une borne inférieure (avec la convention opposée pour l'ensemble vide: 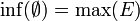 ). Par exemple, tout segment est un ensemble ordonné complet. En revanche,
). Par exemple, tout segment est un ensemble ordonné complet. En revanche,  est complet pour la distance usuelle mais pas en tant qu'ensemble ordonné. Pour éviter toute confusion Bourbaki avait proposé le terme achevé, qui ne s'est pas imposé. Ainsi,
est complet pour la distance usuelle mais pas en tant qu'ensemble ordonné. Pour éviter toute confusion Bourbaki avait proposé le terme achevé, qui ne s'est pas imposé. Ainsi,  n'est pas achevé mais
n'est pas achevé mais 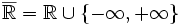 l'est, d'où son nom de droite réelle achevée. Un autre exemple est l'ensemble P(E) des parties d'un ensemble E avec pour ordre l'inclusion: la borne supérieure est la réunion et la borne inférieure l'intersection.Démonstration
l'est, d'où son nom de droite réelle achevée. Un autre exemple est l'ensemble P(E) des parties d'un ensemble E avec pour ordre l'inclusion: la borne supérieure est la réunion et la borne inférieure l'intersection.DémonstrationSoit
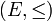 un ensemble ordonné achevé: toute partie de E possède une borne supérieure (y compris l'ensemble vide, ce qui impose que E ait un minimum). Soit A une partie de E et M l'ensemble de ses minorants. Soit c la borne supérieure de M (qui existe car E est achevé). Alors c=inf(A). En effet:
un ensemble ordonné achevé: toute partie de E possède une borne supérieure (y compris l'ensemble vide, ce qui impose que E ait un minimum). Soit A une partie de E et M l'ensemble de ses minorants. Soit c la borne supérieure de M (qui existe car E est achevé). Alors c=inf(A). En effet:- si A est vide, M=E et
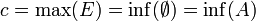
- sinon: supposons que c n'est pas un minorant de A. Alors il existe un élément a de A tel que a<c. Par définition de la borne supérieure, il existe un élément m de M tel que a<m<c, ce qui est impossible car les éléments de M sont les minorants de A. c est donc un minorant de A.
- soit d un minorant de A. Alors d appartient à M donc
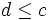 . c est donc le plus grand minorant de A, i.e. c=inf(A).
. c est donc le plus grand minorant de A, i.e. c=inf(A).
L'implication réciproque se démontre de manière analogue.
Par ailleurs, un tel ensemble est un cas particulier de treillis complet. On dispose donc du théorème de Knaster-Tarski : toute application croissante d'un ensemble ordonné achevé dans lui-même possède un point fixe.Voir aussi
- Complété d'un espace métrique sur le site Les-Mathématiques.net
- Espace complet sur le site Les-Mathématiques.net
- Treillis
- Portail des mathématiques
Catégories : Construction classique | Espace métrique - Soit l'espace
Wikimedia Foundation. 2010.