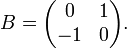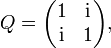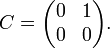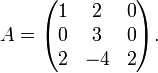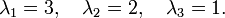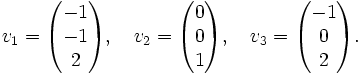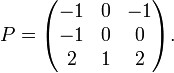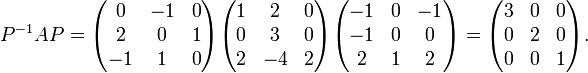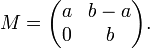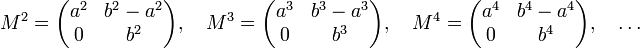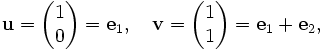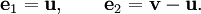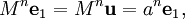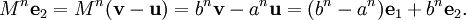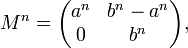Matrice Diagonalisable

Matrice diagonalisable

En algèbre linéaire, une matrice carrée $M$ d'ordre $n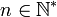$ ( $n\in\mathbb{N}^*$ ) à coefficients dans un corps commutatif $K$ , est dite diagonalisable si elle est semblable à une matrice diagonale, c'est-à-dire s'il existe une matrice inversible $P$ et une matrice diagonale $D$ telles que $P D P - 1 = M$ .

Par exemple, toute matrice diagonale est diagonalisable, il suffit de prendre $P = I n$ (où $I n$ est la matrice identité) dans la définition. Ainsi la matrice nulle est diagonalisable, la matrice identité, les matrices scalaires, ...

Rappelons que si $E$ est un espace vectoriel de dimension finie, alors un endomorphisme $f$ de $E$ est diagonalisable lorsqu'il existe une base de $E$ telle que la matrice de $f$ relativement à cette base soit diagonale.

Notons $can(M)$ , l'endormorphisme de $K n$ canoniquement associé à la matrice $M$ , c'est-à-dire l'application linéaire de $K n$ dans $K n$ qui a pour matrice relativement à la base canonique de $K n$ , la matrice $M$ .

Le concept de changement de base permet de démontrer que la matrice $M$ est diagonalisable si et seulement si $can(M)$ est diagonalisable.

La diagonalisation d'une matrice se ramène donc à la diagonalisation d'un endomorphisme d'un espace vectoriel de dimension finie et réciproquement.

La diagonalisation des matrices (ou des endomorphismes) est intéressante parce que les matrices diagonales sont très faciles à manipuler :

leurs valeurs propres et vecteurs propres se déterminent aisément,
on les élève à des puissances entières en élevant tout simplement leurs coefficients diagonaux à cette puissance, ce qui permet d'en déduire les puissances d'une matrice diagonalisable. Ces puissances représentent le résultat d'applications successives de cette matrice, et sont utiles pour simuler des itérations en analyse numérique. (voir Varga, Matrix Iterative Analysis)

$K$ étant un corps commutatif, nous noterons dans tout l'article 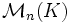$\mathcal{M}_{n}(K)$ l'espace vectoriel des matrices carrées d'ordre $n$ , et 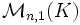$\mathcal{M}_{n,1}(K)$ l'espace vectoriel des matrices à $n$ lignes et une colonne. En diagonalisant une matrice, on se place dans une base où l'on travaille avec une matrice diagonale, ce que simplifie énormément les calculs. Et en général une réduction d'endomorphisme permet de simplifier les calculs. On peut donc faire appel à cette méthode pour les problèmes de résolution de systèmes d'équations linéaires par exemple.

Diagonalisation des matrices

Définitions

Article détaillé : Valeur propre.

Définition 1 — Soit 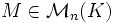$M\in\mathcal{M}_n(K)$ et soit 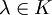$\lambda\in K$ . Le scalaire $λ$ est appelé valeur propre de $M$ , s'il existe un vecteur colonne $X$ non nul de 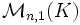$\mathcal{M}_{n,1}(K)$ telle que $M X = λ X$ .

L'ensemble des valeurs propres d'une matrice $M$ s'appelle le spectre de $M$ et est noté généralement $Sp(M)$ ou $Spec(M)$ .

Remarque: Il est important de préciser que le vecteur colonne $X$ doit être non nul, sinon tout scalaire de $K$ serait valeur propre de $M$ puisqu'on a toujours $M 0 = λ0$ !

Définition 2 — Soit 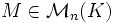$M\in\mathcal{M}_n(K)$ . Un vecteur $X$ non nul de 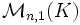$\mathcal{M}_{n,1}(K)$ est appelé vecteur colonne propre ou colonne propre si et seulement s'il existe 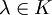$\lambda\in K$ tel que $M X = λ X$ .

On dit alors que $X$ est une colonne propre associée à la valeur propre $λ$ .

Remarque: La condition dans la définition 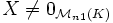$X\neq 0_{\mathcal{M}_{n1}(K)}$ , a pour conséquence qu'un vecteur propre possède une unique valeur propre. Cette condition n'est pas toujours utilisée dans la définition. C'est néanmoins la convention utilisée dans Wikipedia.

Définition 3 — Soit 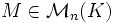$M\in\mathcal{M}_n(K)$ et soit 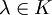$\lambda\in K$ une valeur propre de $M$ . Le sous-espace propre associé à la valeur propre $λ$ est le noyau de l'endomorphisme 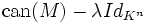${\rm can}(M)-\lambda Id_{K^n}$ . Il est habituellement noté $E λ$ .

Mais il est quelquefois défini comme étant le noyau de la matrice $M - λ I n$ ( $I n$ étant la matrice unité d'ordre $I n$ ), c'est-à-dire l'ensemble:

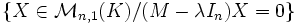$\{X\in\mathcal{M}_{n,1}(K)/(M-\lambda I_n)X=0\}$ ,

aussi égal à

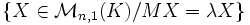$\{X\in\mathcal{M}_{n,1}(K)/MX=\lambda X\}$ .

Ces définitions correspondent exactement à celles données dans le monde des endomorphismes (cf Valeur propre).

Recherche des valeurs propres

Théorème — Considérons une matrice $M$ d'ordre $n$ à coefficients dans un corps commutatif $K$ et 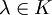$\lambda\in K$ . Les propositions suivantes sont équivalentes:

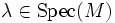$λ$ est valeur propre de $M$ ( $\lambda\in {\rm Spec}(M)$ ),
$M - λ I n$ non inversible,
le système $(M - λ I n) X = 0$ d'inconnue 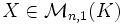$X\in\mathcal{M}_{n,1}(K)$ admet au moins une solution non nulle,
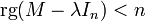$\operatorname{rg}(M-\lambda I_n)<n$ ,
$det(M - λ I n) = 0$ ( $det$ désigne le déterminant d'une matrice).

De ce théorème se déduisent différentes techniques de recherche des valeurs propres. Étant donné un scalaire $λ$ de $K$ , il est possible de déterminer si $M - λ I n$ est inversible ou le rang de $M - λ I n$ en réduisant la matrice par la méthode de Gauss. Cette réduction s'effectue en choisissant si possible, un pivot indépendant de $λ$ afin d'éviter les distinctions de cas.

Il est parfois plus efficace, lorsque la matrice $M - λ I n$ comporte « beaucoup de zéros », de résoudre le système $(M - λ I n) X = 0$ dans lequel $λ$ est considéré comme paramètre, en recherchant les solutions non nulles, ce qui a l'avantage de donner en même temps les vecteurs colonnes propres.

Enfin le calcul du déterminant de $M - λ I n$ peut donner les valeurs propres. Cela revient à déterminer les racines du polynôme caractéristique.

D'autre part, les valeurs propres d'une matrice $M$ , peuvent être obtenues à partir d'un polynôme annulateur $P$ , c'est-à-dire tel que $P (A) = 0$ . Si $λ$ est une valeur propre de $M$ alors $λ$ est racine du polynôme $P$ . La réciproque n'étant pas vraie, il faut déterminer les racines de $P$ pour lesquelles $M - λ I n$ n'est pas inversible. Par exemple, si $A$ est une matrice d'un projecteur, alors $A 2 = A$ donc le polynôme $P (X) = X 2 - X$ est annulateur de $A$ . Les valeurs propres possibles de $A$ sont alors 0 et 1. Mais le projecteur nul, n'admet que 0 comme valeur propre.

Les méthodes de recherche des valeurs propres débouchent sur la détermination de racines de polynômes, ce qui pose généralement des problèmes dans le cas où l'ordre de la matrice est supérieur à 5 à cause de l'absence de formule générale donnant les racines en fonction des coefficients.

Donnons maintenant quelques moyens de détection d'erreurs dans la recherche des valeurs propres.

Nous savons que les sous-espaces propres associés aux différentes valeurs propres d'une matrice $M$ d'ordre $n$ sont en somme directe et donc la somme des dimensions reste inférieure à la dimension de $K n$ . Ainsi une matrice $M$ d'ordre $n$ ne peut admettre plus de $n$ valeurs propres distinctes.
La trace d'une matrice $M$ est un invariant de similitude c'est-à-dire que pour toute matrice inversible $P$ , $tr(P - 1 M P) = tr M$ . Donc la trace d'une matrice $M$ est égale à la somme de ses valeurs propres (comptées avec leur multiplicité). Ainsi lorsqu'une matrice d'ordre $n$ admet $n$ valeurs propres distinctes, la trace constitue une sorte de somme de contrôle.

Recherche des vecteurs colonnes propres

Les colonnes propres associées à une valeur propre $λ$ peuvent être obtenues en résolvant le système $(M - λ I n) X = 0$ , mais la connaissance de la dimension du sous-espace propre associé peut aider à les obtenir plus facilement. Par exemple si on sait qu'il y a $n$ valeurs propres distinctes, alors la dimension des sous-espaces propres est égale à un, et il suffit de trouver une seule colonne non nulle solution du système $(M - λ I n) X = 0$ , les autres lui seront proportionnelles. Si les valeurs propres ont été déterminées en réduisant $M - λ I n$ par la méthode de Gauss, alors le nombre de pivots donne le rang de la matrice et d'après le théorème du rang, la dimension du sous-espace propre associé est égale à $n - rg(M - λ I n)$ .

Méthodes pratiques de diagonalisation

Dans la plupart des cas, il est nécessaire de calculer le polynôme caractéristique de la matrice, afin de déterminer ses valeurs propres et les sous-espaces propres associés :
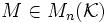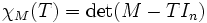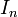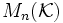Pour $M \in M_n(\mathcal{K})$ le polynôme caractéristique est $\chi_M(T)={\rm det}(M-TI_n)\,$ où $T$ est l'indéterminée et $I_n \,$ est la matrice unité de $M_n(\mathcal{K})$ .
Les valeurs propres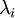 $\lambda_i \,$ sont les racines de 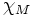$\chi_M \,$ , il y a donc au plus $n \,$ valeurs propres de multiplicité $m_i \,$ .
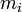On calcule ensuite les sous-espace propres associés à chaque valeur propre:
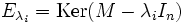
$E_{\lambda _i}={\rm Ker}(M-\lambda _i I_n) \,$
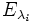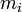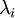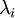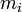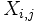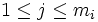La matrice ne sera diagonalisable que si la dimension de chaque sous-espace propre $E_{\lambda _i} \,$ est égale à la multiplicité $m_i \,$ de la valeur propre $\lambda_i \,$ , ce qui signifie que pour chaque $\lambda_i \,$ on a une base de $m_i \,$ vecteurs propres que l'on note $X_ {i,j} \,$ , $1 \le j \le m_i$ .
Alors il existera une matrice inversible $U$ telle que $U - 1 M U$ soit égale à une matrice diagonale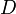 $D\,$ dont les coefficients diagonaux sont les 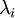$\lambda_i \,$ répétés 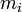$m_i \,$ fois et 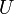$U\,$ sera la matrice dont les colonnes sont les vecteurs 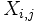$X_ {i,j} \,$ (l'ordre n'a pas d'importance, mais si on a le vecteur 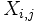$X_ {i,j} \,$ sur la k-ième colonne de 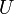$U\,$ , alors on a la valeur propre 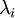$\lambda_i \,$ sur la k-ième colonne de $D\,$ ).
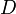Il est aussi possible de déterminer directement les valeurs propres, et des bases des sous-espaces propres associés. La matrice $M$ est diagonalisable si et seulement si la somme des dimensions des différents sous-espaces propres est égale $n$ . Si la matrice est diagonalisable, alors il existe une matrice inversible $P$ obtenue en plaçant les unes à côté des autres, les colonnes propres formant une base de chacun des sous-espaces, et la matrice $D = P - 1 M P$ est alors diagonale. La dimension du sous-espace propre associé à une valeur propre, correspond au nombre de fois que celle-ci est répétée sur la diagonale de la matrice diagonale $D$ semblable à la matrice $M$ .

Propriétés

Les résultats fondamentaux sur la diagonalisation des matrices sont les suivants:

Une matrice $A$ d'ordre $n$ sur un corps commutatif $K$ est diagonalisable si et seulement si la somme des dimensions de ses sous-espaces propres est égale à $n$ , et si et seulement s'il existe une base de 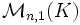$\mathcal{M}_{n,1}(K)$ constituée de vecteurs colonnes propres de $A$ . Si une telle base existe, alors il est possible de former la matrice $P$ ayant comme colonnes ces colonnes propres, $P$ est inversible et $P - 1 A P$ sera alors une matrice diagonale. Les coefficients diagonaux de cette matrice ne sont autres que les valeurs propres de $A$ .
Une matrice peut être diagonalisable sur un corps commutatif $K$ si son polynôme minimal est scindé et que toutes ses racines sont simples, c'est-à-dire s'il est produit de polynômes à coefficients dans $K$ du premier degré distincts. Ce n'est cependant pas une condition nécessaire.

Le résultat suivant, suffisant mais pas nécessaire, est souvent utile:

Une matrice $A$ d'ordre $n$ est diagonalisable sur le corps $K$ si elle a $n$ valeurs propres distinctes dans $K$ , c'est-à-dire si son polynôme minimal a $n$ racines distinctes dans $K$ .

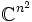En général, sur $\mathbb{C}$ presque toutes les matrices sont diagonalisables. Plus précisément: l'ensemble des matrices complexes d'ordre $n$ qui ne sont pas diagonalisables, considéré comme un sous-ensemble de $\mathbb{C}^{n^2}$ , est un ensemble de mesure nulle pour la mesure de Lebesgue. On peut également signaler que les matrices diagonalisables forment un sous-ensemble dense dans l'ensemble des matrices pour la topologie donnée par n'importe quelle norme matricielle.

Le résultat ne tient pas sur $\mathbb{R}$ . À mesure que $n$ augmente, il devient (dans un certain sens) de moins en moins probable qu'une matrice réelle d'ordre $n$ , aléatoirement choisie, soit diagonalisable sur $\mathbb{R}$ .

Exemples

Exemple 1

Matrices non diagonalisables:

Certaines matrices réelles ne sont pas diagonalisables sur le corps des réels. Considérons par exemple la matrice

$B = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}.$

La matrice $B$ n'a pas de valeurs propres réelles, ainsi il ne peut exister de matrice réelle $Q$ inversible telle que $Q - 1 B Q$ soit une matrice diagonale. Mais, il est possible de diagonaliser $B$ sur le corps des complexes. En prenant,

$Q = \begin{pmatrix} 1 & \textrm{i} \\ \textrm{i} & 1 \end{pmatrix},$

Alors $Q - 1 B Q$ est diagonale.

Cependant, il existe aussi des matrices non diagonalisables, même si le corps des complexes est utilisé. Cela se produit si les multiplicités algébriques et géométriques des valeurs propres ne coïncident pas. Par exemple, considérons:

$C = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}.$

La matrice n'est pas diagonalisable: il n'existe pas de matrice $U$ inversible telle que $U - 1 C U$ soit diagonale. En effet, $C$ a une valeur propre (qui est 0) et cette valeur propre a un ordre de multiplicité algébrique égal à 2 et géométrique égal à 1.

Exemple 2

Considérons la matrice:

$A=\begin{pmatrix} 1 & 2 & 0 \\ 0 & 3 & 0 \\ 2 & -4 & 2 \end{pmatrix}.$

Cette matrice admet comme valeurs propres:

$\lambda_1 = 3, \quad \lambda_2 = 2, \quad \lambda_3= 1.$

Ainsi $A$ qui est de rang 3, a 3 valeurs propres distinctes, donc est diagonalisable.

Si nous voulons diagonaliser $A$ , nous avons besoin de déterminer les vecteurs propres correspondants. Il y a par exemple:

$v_1 = \begin{pmatrix} -1 \\ -1 \\ 2 \end{pmatrix}, \quad v_2 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, \quad v_3 = \begin{pmatrix} -1 \\ 0 \\ 2 \end{pmatrix}.$

On vérifie facilement que $A v k = λ k v k$ .

Maintenant soit $P$ la matrice ayant ces vecteurs propres comme colonnes:

$P= \begin{pmatrix} -1 & 0 & -1 \\ -1 & 0 & 0 \\ 2 & 1 & 2 \end{pmatrix}.$

Alors « $P$ diagonalise $A$ », comme le montre un simple calcul:

$P^{-1}AP = \begin{pmatrix} 0 & -1 & 0 \\ 2 & 0 & 1 \\ -1 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 2 & 0 \\ 0 & 3 & 0 \\ 2 & -4 & 2 \end{pmatrix} \begin{pmatrix} -1 & 0 & -1 \\ -1 & 0 & 0 \\ 2 & 1 & 2 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1\end{pmatrix}.$

Remarquez que les valeurs propres $λ k$ apparaîssent sur la diagonale de la matrice dans le même ordre que nous avons placé les colonnes propres pour former $P$ .

Exemple 3

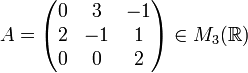
Soit $A= \begin{pmatrix} 0 & 3 & -1 \\ 2 & -1 & 1 \\ 0 & 0 & 2 \end{pmatrix} \in M_3(\mathbb{R})$
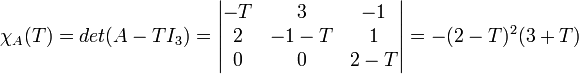$\chi_A(T)=det(A-TI_3)= \begin{vmatrix} -T & 3 & -1 \\ 2 & -1-T & 1 \\ 0 & 0 & 2-T \end{vmatrix}= -(2-T)^2 (3+T)$ (voir le calcul d'un déterminant)
Donc les valeurs propres sont :

2 de multiplicité 2
-3 de multiplicité 1

Calcul des sous-espaces caractéristiques :
Calcul de $E 2$ : On cherche les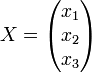 $X = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$ tels que :
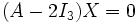
$(A-2I_3)X=0 \,$
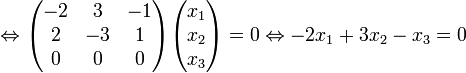
$\Leftrightarrow {\begin{pmatrix} -2 & 3 & -1 \\ 2 & -3 & 1 \\ 0 & 0 & 0 \end{pmatrix}} {\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}} = 0 \Leftrightarrow -2x_1+3x_2-x_3=0$
Donc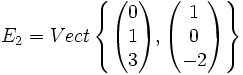 $E_2=Vect \left\{ {\begin{pmatrix} 0 \\ 1 \\ 3 \end{pmatrix}},\begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix} \right\}$
On procède de même pour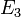 $E_3 \,$ et on obtient :
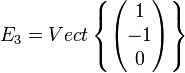
$E_3=Vect \left\{\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} \right\}$
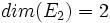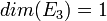On a bien : $dim( E_2 )=2 \,$ et $dim( E_3 )=1 \,$ , donc cette matrice est diagonalisable.
Une diagonalisation possible est :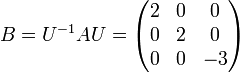 $B=U^{-1}AU={\begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & {-3}\end{pmatrix}}$ , avec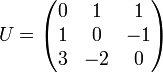 $U = {\begin{pmatrix} 0 & 1 & 1 \\ 1 & 0 & -1 \\ 3 & -2 & 0\end{pmatrix}}$

Les applications

Puissances de matrices

La diagonalisation peut être utilisée pour calculer efficacement les puissances d'une matrice diagonalisable $A$ . Supposons que nous ayons obtenu:

P - 1 A P = D

où $D$ est une matrice diagonale. Alors

A k = (P D P - 1) k = P D k P - 1

et cette dernière puissance est facile à calculer puisque la puissance $k$ ème d'une matrice diagonale s'obtient en élevant les coefficients diagonaux à la puissance $k$ .

Par exemple considérons la matrice suivante:

$M =\begin{pmatrix}a & b-a \\ 0 &b \end{pmatrix}.$

En calculant les différentes puissances de $M$ nous obtenons les formes suivantes:

$M^2 = \begin{pmatrix}a^2 & b^2-a^2 \\ 0 &b^2 \end{pmatrix},\quad M^3 = \begin{pmatrix}a^3 & b^3-a^3 \\ 0 &b^3 \end{pmatrix},\quad M^4 = \begin{pmatrix}a^4 & b^4-a^4 \\ 0 &b^4 \end{pmatrix},\quad \ldots$

Ce phénomène peut être expliqué en diagonalisant $M$ . Pour ce faire, nous avons besoin d'une base de 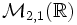$\mathcal{M}_{2,1}(\mathbb{R})$ formée de vecteurs colonnes propres de $M$ . Une telle base de colonnes propres est donnée par:

$\mathbf{u}=\begin{pmatrix} 1 \\ 0 \end{pmatrix}=\mathbf{e}_1,\quad \mathbf{v}=\begin{pmatrix} 1 \\ 1 \end{pmatrix}=\mathbf{e}_1+\mathbf{e}_2,$

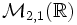où les $e i$ désignent les vecteurs de la base canonique de $\mathcal{M}_{2,1}(\mathbb{R})$ .

L'inverse de la matrice de passage peut s'obtenir à partir de

$\mathbf{e}_1 = \mathbf{u},\qquad \mathbf{e}_2 = \mathbf{v}-\mathbf{u}.$

Un calcul direct montre que

$M\mathbf{u} = a\mathbf{u},\qquad M\mathbf{v}=b\mathbf{v}.$

Ainsi, $a$ et $b$ sont les valeurs propres associées à $u$ et $v$ , repsectivement. D'après la linéairité de la multiplication par une matrice, nous avons donc

$M^n \mathbf{u} = a^n\, \mathbf{u},\qquad M^n \mathbf{v}=b^n\,\mathbf{v}.$

En revenant à la base canonique, nous avons:

$M^n \mathbf{e}_1 = M^n \mathbf{u} = a^n \mathbf{e}_1,$

$M^n \mathbf{e}_2 = M^n (\mathbf{v}-\mathbf{u}) = b^n \mathbf{v} - a^n\mathbf{u} = (b^n-a^n) \mathbf{e}_1+b^n\mathbf{e}_2.$

Les relations précédentes, exprimées sous forme matricielle donnent:

$M^n = \begin{pmatrix}a^n & b^n-a^n \\ 0 &b^n \end{pmatrix},$

ce qui explique le phénomène précédent.

Systèmes Récurrents

Systèmes Différentiels

Équations Différentielles du nième ordre

Voir aussi

Articles en rapport avec les matrices
Par forme	carrée • triangulaire • diagonale • tridiagonale • élémentaire • échelonnée • creuse • aléatoire • circulante • de Hankel • de Toeplitz • de Vandermonde
Transformée	transposée • adjointe • inverse • Comatrice
En relation	équivalente • semblable • congruente
Par propriété	inversible • diagonalisable • trigonalisable • symétrique • antisymétrique • hermitienne • normale • orthogonale • unitaire • symplectique • de Hadamard • définie positive • à diagonale dominante • nilpotente
Par famille	identité • de De Casteljau • de Cartan • de Hilbert • de Mueller • de Pauli • de Dirac
Particulière	CKM
Associée	de permutation • de passage • compagnon • de Sylvester • d'adjacence • laplacienne • hessienne • jacobienne • génératrice • de contrôle • de corrélation • de Gram • de variance-covariance • d'inertie • de Jones • des gains • stochastique
Résultats	décompositions : LU • QR • polaire • valeurs singulières Trigonalisation • Réduction de Jordan • facteurs invariants
Voir aussi	Théorie des matrices • Algèbre linéaire

Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Colinéarité • Indépendance linéaire • Famille libre • Rang • Famille génératrice • Base • Théorème de la base incomplète
Sous-espace	Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension d'un espace vectoriel • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Endomorphisme nilpotent
En dimension finie	Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau

Portail des mathématiques

Ce document provient de « Matrice diagonalisable ».

Catégorie : Matrice

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice Diagonalisable de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Matrice diagonalisable — ● Matrice diagonalisable matrice carrée qui admet une matrice semblable diagonale … Encyclopédie Universelle
Matrice diagonalisable — Exemple de matrice diagonalisable sur le corps des complexes mais pas sur celui des réels, son polynôme caractéristique étant X2 + 1. En mathématiques, une matrice diagonalisable est une matrice carrée semblable à une matrice diagonale. Cette p … Wikipédia en Français
Diagonalisable — Matrice diagonalisable En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et… … Wikipédia en Français
Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice séparable — Matrice semi simple En algèbre linéaire, la notion de matrice semi simple constitue une généralisation de la notion de matrice diagonalisable. Elle permet de discriminer deux types d obstruction à la diagonalisabilité : d une part les… … Wikipédia en Français
diagonalisable — ● diagonalisable adjectif Endomorphisme diagonalisable, endomorphisme pour lequel il existe une base dans laquelle la matrice associée de l endomorphisme est diagonale. Matrice diagonalisable, matrice carrée qui admet une matrice semblable… … Encyclopédie Universelle
Matrice De Transition — Définition Notons l ensemble des applications bornées de E dans On appelle matrice de transition sur E une famille telle que Ainsi, une matrice positive … Wikipédia en Français
Matrice semi-simple — En algèbre linéaire, la notion de matrice semi simple constitue une généralisation de la notion de matrice diagonalisable. Elle permet de discriminer deux types d obstruction à la diagonalisabilité : d une part les obstructions liées à l… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Matrice Diagonalisable

Matrice diagonalisable

Sommaire