- Andre Weil
-
André Weil
Pour les articles homonymes, voir Weil.André Weil 
André Weil (source : AMS) Naissance 6 mai 1906
Paris (France)Décès 6 août 1998
Princeton (États-Unis)Domicile Princeton Nationalité française Champs théorie des nombres, géométrie algébrique Institution Bourbaki, Institute for Advanced Study Diplômé École normale supérieure Célèbre pour conjectures de Weil, cohomologie de faisceaux Distinctions prix Wolf, prix de Kyoto modifier 
André Weil, né le 6 mai 1906 à Paris et mort à Princeton (New Jersey, États-Unis) le 6 août 1998, est une des grandes figures parmi les mathématiciens du XXe siècle. Connu pour son travail fondamental en théorie des nombres et en géométrie algébrique, il fut un des membres fondateurs du groupe Bourbaki. Il est le frère de la philosophe Simone Weil.
Sommaire
Biographie
Né à Paris de parents alsaciens d'origine juive alsacienne et russe qui ont fui la prise de l’Alsace-Lorraine par l'Allemagne, il étudia à Paris, à l'École normale supérieure (S 1922). Il étudia également à Rome et à Göttingen où il reçut son doctorat en 1928. Il passa deux années universitaires à l'université d'Aligarh de 1930 à 1933. Après une année à Marseille, il passa six années à enseigner à Strasbourg. C'est durant cette période qu'il épousa Eveline en 1937.
Lorsque la Seconde Guerre mondiale éclata, Weil se trouvait en Finlande, voyageant en Scandinavie depuis avril 1939. Éveline retourna seule en France. Resté en Finlande, il fut arrêté par les services secrets finlandais, suspecté d'espionnage pour l'URSS. Le prétendu risque qu'il aurait couru d'être fusillé est une exagération[1].
Weil retourna alors en France par la Suède et le Royaume-Uni. Accostant au Havre en janvier 1940, il fut emprisonné à Rouen, de février à mai, sous l'inculpation de s'être soustrait à ses obligations militaires en temps de guerre. Jugé le 3 mai 1940, il fut condamné à cinq ans de prison. Il demanda à être envoyé sur le front et rejoignit alors un régiment à Cherbourg. Après la capitulation française, il revint vers sa famille à Marseille par la mer. Il alla jusqu'à Clermont-Ferrand pour rejoindre son épouse, Eveline, restée en zone occupée. En janvier 1941, ils quittèrent la France face à l'occupant nazi, et partirent pour New York.
Weil travailla à l'Universidade de Sao Paulo de 1945 à 1947, auprès d'Oscar Zariski. Il enseigna à l'Université de Chicago de 1947 à 1958. Il a passé le reste de sa carrière à l'Institute for Advanced Study de Princeton.
Travaux
Il laisse des contributions remarquables dans nombre de domaines, et en premier lieu en géométrie algébrique et en théorie des nombres. Son travail doctoral conduisit au théorème de Mordell-Weil. Il formula l'argument de descente infinie, et pour ce faire, il définit une mesure de la taille des points rationnels d'une variété algébrique ; et il initia la cohomologie galoisienne, qui ne fut appelée ainsi que deux décennies plus tard. Ces deux aspects ont largement été développés depuis pour devenir des objets centraux de la géométrie algébrique actuelle.
Parmi ses plus grands travaux figure la preuve donnée en 1940, en prison, de l'hypothèse de Riemann pour les fonctions zêta des courbes sur les corps finis. Les conjectures de Weil ont largement influencé les géomètres algébristes depuis 1950 ; elles furent prouvées par Bernard Dwork, Alexander Grothendieck (qui, pour les attaquer, mit sur pied un gigantesque programme visant à transférer les techniques de topologie algébrique en théorie des nombres), Michael Artin et enfin Pierre Deligne qui démontra, en 1973, l'hypothèse de Riemann sur les corps finis, partie la plus profonde des conjectures de Weil.
Dans les années 1930, il fournit une preuve du théorème de Riemann-Roch, à la suite des travaux de Claude Chevalley.
En topologie générale, il introduit le concept d'espace uniforme. Son travail sur les faisceaux fut très peu publié, mais apparut dans ses correspondances avec Henri Cartan à la fin des années 1940.
Plus basiquement, il a introduit la notation
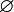pour l'ensemble vide.Œuvres
Ses livres eurent une grande influence sur la recherche. Alexander Grothendieck s'est plaint de l'aridité des Foundations of Algebraic Geometry. Les écrits de Weil se placent dans le courant de la littérature mathématique d'après-guerre.
- Arithmétique et géométrie sur les variétés algébriques (1935)
- Sur les espaces à structure uniforme et sur la topologie générale (1937)
- L'intégration dans les groupes topologiques et ses applications (1940)
- Foundations of Algebraic Geometry (1946)
- Sur les courbes algébriques et les variétés qui s’en déduisent (1948)
- Variétés abéliennes et courbes algébriques (1948)
- Introduction à l'étude des variétés kählériennes (1958)
- Discontinuous subgroups of classical groups (1958) Chicago lecture notes
- Basic Number Theory (1967)
- Dirichlet Series and Automorphic Forms, Lezioni Fermiane (1971) Lecture Notes in Mathematics, vol. 189,
- Essais historiques sur la théorie des nombres (1975)
- Elliptic Functions According to Eisenstein and Kronecker (1976)
- Œuvres Scientifiques, Collected Works, three volumes (1979)
- Number Theory for Beginners (1979) with Maxwell Rosenlicht
- Adeles and Algebraic Groups (1982)
- Number Theory: An Approach Through History From Hammurapi to Legendre (1984)
- Souvenirs d’apprentissage, Birkhäuser (1991)
Bibliographie
- Sylvie Weil, Chez les Weil, Buchet-Chastel, Paris, 2009.
Distinctions
Il a reçu de nombreuses distinctions académiques dont le Prix Wolf de Mathématiques en 1979 et le Prix de Kyōto en 1994. Il a été membre honoraire de la London Mathematical Society, élu à l'académie des sciences de Paris et à la National Academy of Sciences aux États-Unis.
À sa mort, le seul honneur mentionné dans sa biographie officielle indiquait simplement « Membre, Académie des Sciences et des Lettres de Poldavie », un pays imaginaire où aurait enseigné le tout aussi imaginaire mathématicien Nicolas Bourbaki.
Notes et références
- ↑ Voir l'article d'Osmo Pekonen, « L'affaire Weil à Helsinki en 1939 », paru dans Gazette des mathématiciens, n°52 (avril 1992), pp. 13-20, avec un épilogue par Weil lui-même.
Articles connexes
- Cohomologie de Weil
- Conjectures de Weil
- Diviseur de Weil
- Théorie de Chern-Weil
- Loi de réciprocité de Weil
- Théorème de Mordell-Weil
- Conjecture de Shimura-Taniyama-Weil
- Conjecture de Hasse-Weil
Lien externe
Portail des mathématiques
Catégories : Bourbaki | Mathématicien français | Ancien élève de l'École normale supérieure (rue d'Ulm) | Naissance en 1906 | Naissance à Paris | Décès en 1998 | Géomètre | Membre de l'Académie des sciences (France)
Wikimedia Foundation. 2010.
