- Groupe Simple
-
Groupe simple
En mathématiques, un groupe simple est un groupe qui ne possède pas de sous-groupe distingué autre que trivial.
Sommaire
Définition
Soit (G, * ) un groupe. On dit qu'il s'agit d'un groupe simple s'il n'a pas de sous-groupe distingué mis à part ({e}, * ) (e étant l’élément neutre du groupe) et (G, * ) lui-même.
Exemples
Quelques exemples de groupes simples :
- Les seuls groupes abéliens simples hormis le groupe trivial sont les groupes cycliques d'ordre premier.
DémonstrationEn effet, tout sous-groupe d'un groupe commutatif G est normal.
Ainsi, si g est un élément de G autre que le neutre, le sous-groupe qu'il engendre est nécessairement G lui-même.
Si G est non trivial, alors G est monogène. S'il est infini, il est isomorphe à
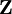et contient le sous-groupe strict 
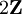. Sinon, il est cyclique d'ordre n ; et à tout diviseur strict éventuel de n correspond un sous-groupe non trivial. Donc, n est nécessairement premier.
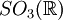, le groupe des matrices spéciales orthogonales d'ordre 3 à coefficients réels, muni du produit matriciel.
- Pour
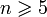, le groupe alterné sur n éléments An. Ce résultat est à la base de la théorie de la résolution par radicaux.
- De nombreux groupes de type Lie sont simples. C'est le cas, par exemple du groupe simple d'ordre 168 qui peut être vu comme le groupe linéaire d'un espace vectoriel de dimension 3 sur le corps fini à deux éléments.
- Les groupes sporadiques.
Intérêt
Le terme « simple » signifie que de tels groupes ne sont pas, en quelque sorte, « réductibles » à un groupe plus maniable. L'intérêt d'un sous-groupe distingué non trivial H d'un groupe G est souvent de permettre la construction du groupe quotient G / H. L'étude de G se ramène alors à celle de H et de G / H. Cette construction n'est pas possible pour un groupe simple et on ne peut donc pas ramener son étude à celle d'un groupe quotient de cardinal plus petit que lui.
Les groupes simples finis sont importants car il peuvent être perçus comme les briques de base de tous les groupes finis, de la même façon que tous les nombres entiers peuvent être décomposés en produit de nombres premiers.
La classification des groupes simples finis fut achevée en 1982.
Théorème de Feit–Thompson
Tout groupe fini d’ordre impair est résoluble.
Il en résulte que tout groupe fini simple non abélien est d’ordre pair et contient donc au moins une involution ( c'est à dire un élément d'ordre 2 ).
Voir aussi
Portail des mathématiques
Catégorie : Théorie des groupes
Wikimedia Foundation. 2010.
