Médiane (géométrie)

Pour les articles homonymes, voir Médiane.

Dans son sens le plus courant, une médiane désigne, dans un triangle, une droite joignant un des sommets du triangle au milieu du côté opposé.

Par extension, en géométrie plane, les médianes d'un quadrilatère sont les segments reliant les milieux de deux côtés opposés.

Enfin, en géométrie dans l'espace, les médianes d'un tétraèdre sont les droites passant par un sommet du tétraèdre et par l'isobarycentre des trois autres.

Géométrie du triangle

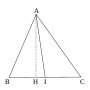
Dans un triangle ABC, la médiane issue du sommet A est la droite (A I ) où I désigne le milieu du segment [B, C ]. Le terme médiane désigne parfois le segment [A, I ] plutôt que la droite (A I ).

Chaque médiane sépare le triangle ABC en deux triangles d'aires égales: l'aire du triangle ABI est égale à l'aire du triangle ACI .

(Pour l'image agrandie, voir la démonstration).

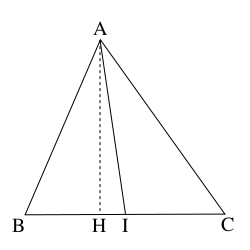
Démonstration

L'aire du triangle ABI est égale à l'aire du triangle ACI .

Considérons les deux triangles ABI et ACI .

On appelle H le projeté orthogonal du point A sur la droite (B C ).

Comme I est le milieu du segment [B, C ], on a BI = CI .

L'aire du triangle ABI est égale à . L'aire du triangle ACI est égale à . Comme BI = CI , ces deux aires sont égales^[1].

On démontre de la même manière que les médianes issues de B et de C vérifient cette propriété.

1. ↑ Une autre façon élémentaire de le démontrer est de remarquer que ces deux triangles sont les moitiés de deux parallélogrammes de côté commun (AI ) et translatés l'un de l'autre.

Théorème de la médiane

Dans le triangle ABC, si I est le milieu de [B, C ] alors Ce théorème est une conséquence immédiate de la définition de I comme isobarycentre de B et C (voir l'article barycentre).

Le « deuxième théorème de la médiane » affirme que

Il fut énoncé par Apollonius de Perga et par Thalès.

Isobarycentre

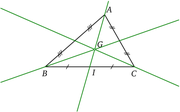
Les trois médianes d'un triangle sont concourantes. Leur point d'intersection est l'isobarycentre des trois sommets, souvent appelé « centre de gravité du triangle ». Il est situé aux deux tiers de chaque médiane à partir du sommet correspondant. Cet isobarycentre G vérifie la relation vectorielle :

(Pour voir l'image agrandie, dérouler la démonstration ci-dessous).

Démonstration

Médianes d'un triangle et isobarycentre des trois sommets

Le milieu I de [B, C ] est défini par l'équation vectorielle :

L'isobarycentre G des trois points A, B et C est défini par l'équation vectorielle :

De ces deux équations on déduit :

Par conséquent G, A et I sont alignés, autrement dit G appartient à la médiane (AI ). On démontre de même qu'il appartient aux deux autres médianes. Les trois médianes sont donc bien concourantes. (On peut voir aussi cette propriété comme un cas particulier du théorème de Ceva.)

Médiane dans des triangles particuliers

Médiane dans un triangle rectangle

Dans un triangle isocèle, la médiane relative à la base du triangle est un axe de symétrie du triangle. Considérées comme des segments, les deux autres médianes sont de longueur égale. Réciproquement si dans un triangle deux médianes sont de même longueur, le triangle est isocèle.

Dans un triangle rectangle, la médiane issue du sommet de l'angle droit mesure la moitié de l'hypoténuse. Réciproquement si dans un triangle la longueur d'une médiane est égale à la moitié de la longueur du côté correspondant, le triangle est rectangle.

Médianes dans un quadrilatère

Médianes d'un quadrilatère

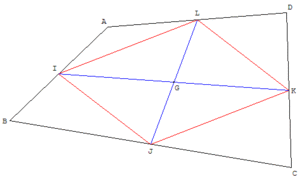
Les médianes du quadrilatère sont les segments reliant les milieux des côtés opposés.

• Les médianes sont les diagonales du parallélogramme de Varignon, elles se coupent en leurs milieux.

• L'associativité des barycentres permet aussi de justifier que le milieu des médianes est l'isobarycentre des sommets du quadrilatère. Contrairement au cas du triangle, cet isobarycentre des sommets ne coïncide pas avec le centre de masse.

Géométrie, dans l'espace

Le tétraèdre régulier de la molécule de méthane

En géométrie dans l'espace, on appelle médianes d'un tétraèdre les droites joignant un des sommets du tétraèdre et l'isobarycentre des trois autres. Il y a donc quatre médianes dans un tétraèdre. Elles se coupent en un point qui est l'isobarycentre des quatre sommets. Toutes ces propriétés sont des conséquences de l'associativité du barycentre.

Dans un tétraèdre régulier (dont toutes les faces sont des triangles équilatéraux), les médianes sont aussi les hauteurs. On dira que ce tétraèdre est orthocentrique car ses hauteurs sont concourantes (ce n'est pas le cas, en général, dans un tétraèdre, contrairement à un triangle).

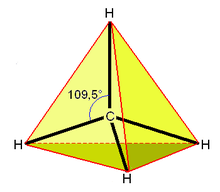
La molécule de méthane CH₄ illustre ce cas : les sommets sont occupés par des atomes d'hydrogène ; l'atome de carbone se situe au point de rencontre des médianes.

• Portail de la géométrie