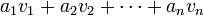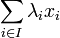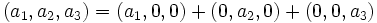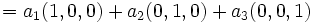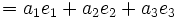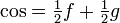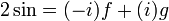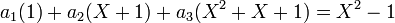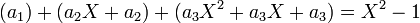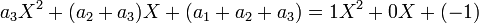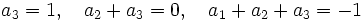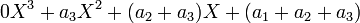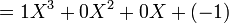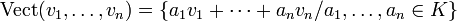Combinaison Linéaire

En mathématiques, les combinaisons linéaires sont un concept central de l'algèbre linéaire et d'autres domaines des mathématiques connexes. La majeure partie de cet article traite des combinaisons linéaires dans le contexte d'espace vectoriel sur un corps commutatif, et indique quelques généralisations à la fin de l'article.

Sommaire 1 Définitions 2 Exemples et contre-exemples 2.1 Géométrie analytique 2.2 Analyse fonctionnelle 2.3 Géométrie algébrique 3 Sous-espace vectoriel engendré 4 Autres concepts relatifs 5 Généralisations 6 Voir aussi

Définitions

Supposons que K soit un corps commutatif et E un espace vectoriel sur K. Comme d'habitude nous appelons les éléments de E les vecteurs et les éléments de K les scalaires. Si 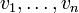sont des vecteurs de E et 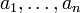des scalaires, alors la combinaison linéaire de ces vecteurs ayant comme coefficients ces scalaires est:

Par convention, une combinaison linéaire ne portant sur aucun vecteur est déclarée nulle.

On peut souhaiter parler de combinaison linéaire sur une infinité de termes ; on convient alors que tous les scalaires intervenant soient nuls sauf un nombre fini : 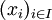étant une famille quelconque de vecteurs de E et 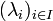une famille de scalaires presque tous nuls (c'est-à-dire tous nuls sauf éventuellement un nombre fini), la combinaison linéaire de la famille 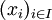de coefficients 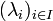est la somme suivante:

Une relation de dépendance linéaire est une combinaison linéaire égale au vecteur nul. La relation de dépendance linaire triviale est celle donnée par une famille de coefficients tous nuls.

Exemples et contre-exemples

Géométrie analytique

Soit K le corps des nombres réels, et soit E l'espace vectoriel euclidien .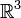

Considérons les vecteurs e₁ = (1,0,0), e₂ = (0,1,0) et e₃ = (0,0,1).

Alors tout vecteur de 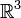est une combinaison linéaire de e₁, e₂ et e₃.

Pour le démontrer, considérons un vecteur arbitraire (a₁,a₂,a₃) de 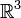, et écrivons:

Analyse fonctionnelle

Soit K l'ensemble de tous les nombres complexes, et soit E l'ensemble 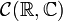des fonctions continues de la droite réelle dans le plan complexe .

Considérons les vecteurs (fonctions) f et g définies par f(t) = e^it et g(t) = e ^{− it}.

(Ici, e désigne la base du logarithme néperien, approximativement égale à 2,71828, et i le nombre imaginaire.

Des combinaisons linéaires de f et g sont:

• 
• 

Par contre, la fonction constante 3 n'est pas une combinaison linéaire de f et g. Pour le voir, supposons par l'absurde que 3 puisse être écrite comme combinaison linéaire des fonctions 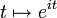et 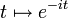. Cela signifierait qu'il existerait des scalaires complexes a et b tels que pour tout réel t, ae^it + be ^{− it} = 3. En posant t = 0 et t = π, cela donnerait les relations a + b = 3 et a + b = − 3, qui ne pourraient clairement se produire.

Géométrie algébrique

Soit K un corps commutatif quelconque ( ou ), et E l'ensemble K[X] des polynômes à coefficients dans le corps K.

Considérons les vecteurs (polynômes) p₁ = 1, p₂ = X + 1 et p₃ = X² + X + 1.

Le polynôme X² − 1 est-il combinaison linéaire de p₁, p₂ et p₃ ?

Pour le voir, considérons une combinaison linéaire arbitraire de ces vecteurs et essayons de voir quand est-ce qu'elle est égale à ce vecteur X² − 1.

Prenons, des coefficients arbitraires a₁,a₂ et a₃. Nous voulons:

En distribuant les coefficients sur les polynômes nous obtenons

et regroupons selon les puissance de X, nous obtenons

Deux polynômes sont égaux si et seulement si leurs coefficients correpondants sont égaux, ainsi nous pouvons en déduire que

Ce système d'équations linéaires peut facilement être résolu.

Tout d'abord, la première équation montre que a₃ = 1.

Sachant cela, nous pouvons résoudre la deuxième équation qui donne a₂ = − 1.

Finalement, la dernière équation nous indique que a₁ vaut aussi − 1.

Réciproquement, l'égalité 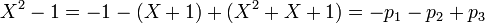est bien vérifiée. Ainsi X² − 1 est combinaison linéaire de p₁,p₂ et p₃.

Par conséquent, X² − 1 s'écrit d'une seule manière possible sous forme d'une combinaison linéaire de p₁,p₂ et p₃.

D'autre part, qu'en est-il du polynôme X³ − 1 ?

Si nous essayons d'écrire ce vecteur comme une combinaison linéaire de p₁,p₂ et p₃, alors en suivant le même raisonnement qu'avant, nous obtenons l'équation:

Cependant, lorsque nous traduisons que les coefficients correspondants doivent être égaux dans ce cas-ci, la relation obtenue en considérant X³ devient

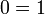qui est contradictoire.

Par conséquent, il n'y a aucune manière pour que ceci soit vrai, ainsi X³ − 1 n'est pas combinaison linéaire de p₁,p₂ et p₃.

Sous-espace vectoriel engendré

Considérons un corps commutatif K et un espace vectoriel E arbitraires, et soit 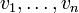des vecteurs de E. Il est intéressant de considérer l'ensemble de toutes les combinaisons linéaires de ces vecteurs. Cet ensemble s'appelle le « sous-espace vectoriel engendré » (ou juste « sous-espace engendré ») par ces vecteurs, disons par l'ensemble 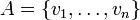. Notons 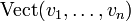ou < A > l'ensemble

Autres concepts relatifs

Parfois, un certain vecteur peut être écrit dans deux manières différentes comme combinaison linéaire de 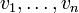. Si cela se produit alors les vecteurs 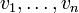sont linéairement dépendants, et dans le cas contraire, lorsque toute écriture d'un vecteur comme combinaison linéaire de 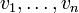est unique, alors les vecteurs sont linéairement indépendants.

De même, nous pouvons parler de la dépendance ou de l'indépendance linéaire des vecteurs d'un ensemble arbitraire A. Si les vecteurs de A sont linéairement indépendants alors la partie A est dite libre et si de plus le sous-espace vectoriel engendré par A est égal à E alors A est une partie basique de E.

Nous pouvons assimiler les combinaisons linéaires à l'opération la plus générale possible sur un espace vectoriel. Les opérations de base d'addition et de multiplication par un scalaire, ainsi que l'existence d'un élément neutre et d'opposés, ne peuvent pas être combinées de manière plus compliquée qu'en une combinaison linéaire. Finalement, ce fait se trouve au cœur de l'utilité des combinaisons linéaires dans l'étude des espaces de vecteur.

Généralisations

Si E est un espace vectoriel topologique, alors il est possible de donner un sens à une combinaison linéaire infinie, en utilisant la topologie de E. Par exemple, nous pourrions parler de la somme infinie .

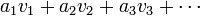De telles combinaisons linéaires infinies n'ont pas toujours un sens; nous les qualifions de convergentes lorsqu'elles en ont un. Le fait de pouvoir considérer davantage de combinaisons linéaires dans ce cas peut également mener à des concepts plus larges de sous-espace vectoriel engendré, d'indépendance linéaire, et de bases.

Si K est un anneau commutatif au lieu d'être un corps, alors tout ce qui a été dit au-dessus sur les combinaisons linéaires se généralise sans aucun changement. La seule différence est que nous appelons ces espaces E des modules au lieu d'espaces vectoriels.

Si K est un anneau non commutatif, alors la notion de combinaison linéaire se généralise encore, cependant avec une restriction: Puisque les modules sur les anneaux non commutatifs peuvent être des modules à droite ou à gauche, nos combinaisons linéaires peuvent également être écrites à droite ou à gauche, c'est-à-dire avec des scalaires placés à droite ou à gauche, selon la nature du module. C'est simplement une question de multiplication par un scalaire du bon côté.

Une adaptation plus compliquée survient lorsque E est un bimodule sur deux deux anneaux, K_G et K_D.

Dans ce cas, la combinaison linéaire la plus générale ressemble à:

où 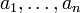appartiennent à K_G, 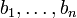appartiennent à K_D, et 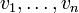appartiennent à E.

Voir aussi

Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Colinéarité • Indépendance linéaire • Famille libre • Rang • Famille génératrice • Base • Théorème de la base incomplète
Sous-espace	Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension d'un espace vectoriel • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Endomorphisme nilpotent
En dimension finie	Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau

• Portail des mathématiques