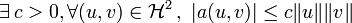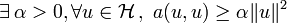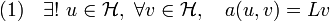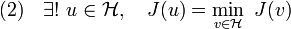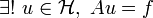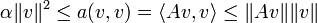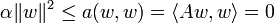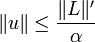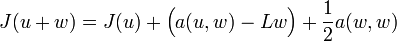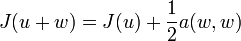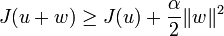Theoreme de Lax-Milgram

Théorème de Lax-Milgram

Le théorème de Lax-Milgram – des noms de Peter Lax et Arthur Milgram – est un théorème de mathématiques. Il est utilisé pour résoudre des équations différentielles partielles via la formulation faible et sert ainsi notamment de fondement à la méthode des éléments finis.

Énoncé

Soient :

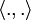$\mathcal{H}$ un espace de Hilbert réel muni de son produit scalaire noté $\langle.,.\rangle$ , de norme associée notée $\|.\|$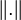
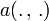une forme bilinéaire qui est
- continue sur $\mathcal{H}\times\mathcal{H}$ : $\exists\,c>0, \forall (u,v)\in \mathcal{H}^2\,,\ |a(u,v)|\leq c\|u\|\|v\|$
- coercive sur $\mathcal{H}$ (certains auteurs disent plutôt $\mathcal{H}$ -elliptique) : $\exists\,\alpha>0, \forall u\in\mathcal{H}\,,\ a(u,u) \geq \alpha\|u\|^2$
$L$ une forme linéaire continue sur $\mathcal{H}$ .

Sous ces hypothèses il existe un unique $u$ de $\mathcal{H}$ tel que l'équation $a (u, v) = L v$ soit vérifiée pour tout $v$ de $\mathcal{H}$ :

$(1) \quad \exists!\ u \in \mathcal{H},\ \forall v\in\mathcal{H},\quad a(u,v)=Lv$

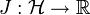Si de plus la forme bilinéaire $a$ est symétrique, alors $u$ est l'unique élément de $\mathcal{H}$ qui minimise la fonctionnelle $J:\mathcal{H}\rightarrow\R$ définie par 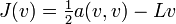$J(v) = \tfrac{1}{2}a(v,v)-Lv$ pour tout $v$ de $\mathcal{H}$ , c'est-à-dire :

$(2) \quad \exists!\ u \in \mathcal{H},\quad J(u) = \min_{v\in\mathcal{H}}\ J(v)$

Démonstration

Cas général

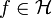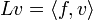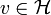Par application du théorème de Riesz sur les formes linéaires continues, il existe un unique $f\in\mathcal{H}$ tel que $Lv=\langle f,v\rangle$ pour tout $v\in\mathcal{H}$ .

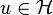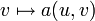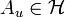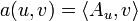Pour tout $u\in\mathcal{H}$ , l'application $v\mapsto a(u,v)$ est une forme linéaire continue sur $\mathcal{H}$ et donc de la même manière, il existe un unique élément $A_u\in\mathcal{H}$ tel que $a(u,v)=\langle A_u,v\rangle$ pour tout 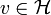$v\in\mathcal{H}$ . On montre facilement que l'opérateur 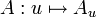$A:u\mapsto A_u$ ainsi défini est un endomorphisme linéaire continu sur $\mathcal{H}$ . La relation $(1)$ s'écrit donc de manière équivalente :

$\exists!\ u \in \mathcal{H},\ Au=f$

Pour prouver cette proposition, il suffit donc de montrer que $A$ est une bijection de $\mathcal{H}$ sur $\mathcal{H}$ . On montre dans un premier temps que l'opérateur est injectif, puis qu'il est surjectif.

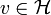
Par la coercivité de $a$ et en appliquant l'inégalité de Cauchy-Schwarz, on a pour tout $v\in\mathcal{H}$

$\alpha\|v\|^2 \leq a(v,v) = \langle Av,v\rangle \leq \|Av\|\|v\|$

d'où 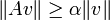$\|Av\| \geq \alpha\|v\|$ pour tout $v$ de $\mathcal{H}$ (*), ce qui montre que $A$ est injectif.

Pour la surjectivité, considérons 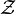$\mathcal{Z}$ l'image de l'opérateur $A$ dans $\mathcal{H}$ .

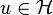L'inégalité (*) implique que, si $A u n$ est une suite de Cauchy, alors $u n$ est une suite de Cauchy, dans $\mathcal{H}$ complet donc converge vers $u \in \mathcal{H}$ . Et $A$ est continue, donc $A u n$ converge vers $A u$ .

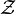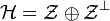$\mathcal{Z}$ est donc un sous-espace fermé de $\mathcal{H}$ et par le théorème du supplémentaire orthogonal d'un fermé on sait que $\mathcal{H}= \mathcal{Z} \oplus \mathcal{Z}^{\perp}$ .

Soit ensuite un élément $w$ de 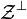$\mathcal{Z}^{\perp}$ , on a par définition 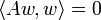$\langle Aw,w\rangle = 0$ et donc :

$\alpha\|w\|^2 \leq a(w,w) = \langle Aw,w\rangle = 0$

d'où $w = 0$ . Ainsi, 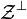$\mathcal{Z}^{\perp}$ est réduit à ${0}$ , ce qui montre que $A$ est surjectif.

L'endomorphisme $A$ est bijectif, il existe donc un unique $u$ de $\mathcal{H}$ tel que $A u = f$ et il est donné par $u = A - 1 f$ .

Remarque

Sans calculer $u$ on a l'inégalité

$\|u\| \leq \frac{\|L\|'}{\alpha}$

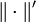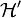où $\|\cdot\|'$ désigne la norme de l'espace dual $\mathcal{H}'$ .

Cas symétrique

Si la forme bilinéaire $a$ est symétrique, on a pour tout $w$ de $\mathcal{H}$ :

$J(u+w) = J(u)+\Big(a(u,w)-Lw\Big)+\frac{1}{2}a(w,w)$

Comme $u$ est l'unique solution de la proposition (1), cela donne

$J(u+w) = J(u)+\frac{1}{2}a(w,w)$

Et comme $a$ est coercive, on a :

$J(u+w) \geq J(u) + \frac{\alpha}{2}\|w\|^2$

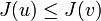On a donc $J(u) \leq J(v)$ pour tout 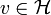$v\in\mathcal{H}$ , d'où le résultat $(2)$ .

Applications

Ce théorème est à la base des méthodes aux éléments finis, on peut en effet montrer que si au lieu de chercher u dans l'on cherche u_n dans 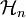, un sous espace de de dimension finie n, alors d'une part :
- Dans le cas où $a$ est symétrique $u n$ est le projeté de $u$ au sens du produit scalaire définit par $a$
- Si l'on se donne 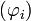$(\varphi_i)$ une base de 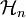$\mathcal{H}_n$ , le problème se ramène alors à la résolution d'un système linéaire :

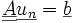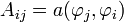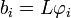
$\underline{\underline{A}} \underline{u_n} = \underline{b}$ avec $A_{ij}=a(\varphi_j,\varphi_i)$ et $b_i=L\varphi_i$

Articles de mathématiques en rapport avec l'algèbre bilinéaire

Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz

modifier

Articles de mathématiques en rapport avec l'analyse fonctionnelle
Fonctionnelle • Calcul des variations • Dérivée fonctionnelle • Espace de Banach • Algèbre de Banach • Espace de Hilbert • Espace de Fréchet • Variété banachique • Espace de fonctions • Noyau reproduisant • Série de Fourier • Transformée de Fourier • Distribution • Topologie faible

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Lax-Milgram ».

Catégories : Théorème d'analyse | Espace de Hilbert

Wikimedia Foundation. 2010.

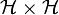Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Lax-Milgram de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Théorème de lax-milgram — Le théorème de Lax Milgram – des noms de Peter Lax et Arthur Milgram – est un théorème de mathématiques. Il est utilisé pour résoudre des équations différentielles partielles via la formulation faible et sert ainsi notamment de fondement à la… … Wikipédia en Français
Théorème de Lax-Milgram — Le théorème de Lax Milgram – des noms de Peter Lax et Arthur Milgram (en) – est un théorème de mathématiques s appliquant à certains problèmes aux dérivées partielles exprimés sous une formulation faible (appelée également formulation… … Wikipédia en Français
Lemme de Lax-Milgram — Théorème de Lax Milgram Le théorème de Lax Milgram – des noms de Peter Lax et Arthur Milgram – est un théorème de mathématiques. Il est utilisé pour résoudre des équations différentielles partielles via la formulation faible et sert ainsi… … Wikipédia en Français
Theoreme de Stampacchia — Théorème de Stampacchia Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
Théorème de stampacchia — Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
Theoreme de Hille-Yosida — Théorème de Hille Yosida En théorie des semi groupes, le théorème de Hille Yosida est un outil puissant et fondamental reliant les propriétés de dissipation de l énergie d un opérateur non borné à l existence unicité et la régularité des… … Wikipédia en Français
Theoreme de projection sur un convexe ferme — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… … Wikipédia en Français
Théorème de projection orthogonale sur un convexe — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… … Wikipédia en Français
Theoreme de Hahn-Banach — Théorème de Hahn Banach Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais… … Wikipédia en Français
Théorème de hahn-banach — Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais limitées partout). En… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Theoreme de Lax-Milgram

Théorème de Lax-Milgram

Sommaire

Énoncé