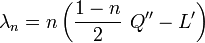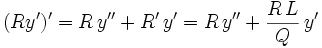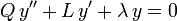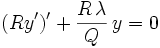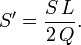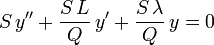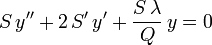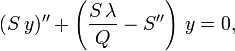- Polynomes orthogonaux
-
Polynômes orthogonaux
Sommaire
Introduction
En mathématiques, une suite de polynômes orthogonaux est une suite infinie de polynômes p0(x), p1(x), p2(x) ... , dans laquelle chaque pn(x) a un degré n et de telle sorte que les polynômes de la suite sont orthogonaux deux à deux pour un produit scalaire de fonctions donné.
- Le produit scalaire de fonctions le plus simple est l'intégrale du produit de ces fonctions:
- Plus généralement, nous pouvons introduire une "fonction poids" W(x) dans l'intégrale (W doit être positive sur l'intervalle d'intégration):
- Avec cette définition du produit scalaire, deux fonctions sont orthogonales entre elles si leur produit scalaire est égal à zéro (de la même manière que deux vecteurs sont orthogonaux (perpendiculaires) si leur produit scalaire égale zéro). On introduit alors la norme associée :
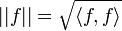 ; le produit scalaire fait de l'ensemble de toutes les fonctions de norme finie un espace de Hilbert.
; le produit scalaire fait de l'ensemble de toutes les fonctions de norme finie un espace de Hilbert.
L'intervalle d'intégration est appelé intervalle d'orthogonalité. Il peut être infini à une ou deux bornes.
Le domaine des polynômes orthogonaux a été développé durant le XIXème siècle par l'étude des fractions continues par Stieltjes. En a découlé de multiples applications en mathématiques et en physique.
Exemple : les polynômes de Legendre
Les polynômes orthogonaux les plus simples sont les polynômes de Legendre pour lesquels l'intervalle d'orthogonalité est [−1, 1] et la fonction poids est simplement la fonction constante de valeur 1. Ils sont la base orthogonale adaptée au drapeau
![(\mathbb{R}_i[x])_{0\leq i\leq n}](/pictures/frwiki/51/36bbd2bb8acfbe47294b2ac3481c0f6c.png) :
:Ils sont tous orthogonaux sur [−1, 1]:
Propriétés des suites de polynômes orthogonaux
Dans le cas général, on définit un produit scalaire par la formule analogue :
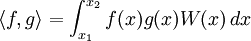 , où la fonction poids W doit être strictement positive dans le domaine d'intégration. Dans certains cas, elle peut être nulle ou infinie aux bornes de l'intégrale. L'intégrale du produit de la fonction poids par un polynôme doit être finie.
, où la fonction poids W doit être strictement positive dans le domaine d'intégration. Dans certains cas, elle peut être nulle ou infinie aux bornes de l'intégrale. L'intégrale du produit de la fonction poids par un polynôme doit être finie.Toute suite de polynômes
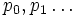 , où chaque
, où chaque 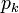 est de degré k, est une base de l'espace vectoriel (de dimension infinie) de tous les polynômes. Une suite de polynômes orthogonaux est simplement une suite qui forme une base orthogonale pour cet espace, relativement à ce produit scalaire.
est de degré k, est une base de l'espace vectoriel (de dimension infinie) de tous les polynômes. Une suite de polynômes orthogonaux est simplement une suite qui forme une base orthogonale pour cet espace, relativement à ce produit scalaire.Le procédé de Gram-Schmidt peut transformer toute base d'un espace vectoriel (muni d'un produit scalaire) en une base orthogonale. On démarre avec un vecteur de la base et on ajoute, un à un, de nouveaux vecteurs de telle manière que chacun soit orthogonal à tous les précédents, en soustrayant au vecteur suivant de la base initiale une combinaison linéaire des précédents vecteurs (c'est un exercice souvent proposé dans les cours d'algèbre linéaire). C'est ainsi qu'on a construit les polynômes de Legendre au paragraphe précédent.
Quand on construit une base orthogonale, on peut être tenté de la rendre orthonormale, c'est-à-dire telle que
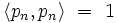 pour tout n, en divisant chaque pn par sa norme. Dans le cas des polynômes, il en résulterait souvent des coefficients contenant des racines carrées. On préfère souvent choisir un multiplicateur tel que les coefficients restent rationnels, et donnent des formules aussi simples que possible. On appelle cela standardisation. Les polynômes "classiques" énumérés ci-dessous ont été ainsi standardisés ; typiquement, le coefficient de leur terme de plus haut degré ont été mis à une quantité donnée (1 pour les polynômes de Legendre). Cette standardisation n'a pas de signification mathématique, c'est juste une convention, qui pourrait aussi parfois être obtenue par une mise à l'échelle de la fonction poids correspondante. Notons
pour tout n, en divisant chaque pn par sa norme. Dans le cas des polynômes, il en résulterait souvent des coefficients contenant des racines carrées. On préfère souvent choisir un multiplicateur tel que les coefficients restent rationnels, et donnent des formules aussi simples que possible. On appelle cela standardisation. Les polynômes "classiques" énumérés ci-dessous ont été ainsi standardisés ; typiquement, le coefficient de leur terme de plus haut degré ont été mis à une quantité donnée (1 pour les polynômes de Legendre). Cette standardisation n'a pas de signification mathématique, c'est juste une convention, qui pourrait aussi parfois être obtenue par une mise à l'échelle de la fonction poids correspondante. Notons 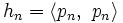 (la norme de
(la norme de 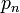 est la racine carrée de
est la racine carrée de  ). Les valeurs de
). Les valeurs de  pour les polynômes standardisés sont énumérées dans le tableau ci-dessous. Nous avons
pour les polynômes standardisés sont énumérées dans le tableau ci-dessous. Nous avons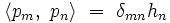 ;
;
où δmn est le delta de Kronecker.
Toute suite de polynômes orthogonaux possède un grand nombre de propriétés élégantes. Pour commencer :
Lemme 1: Étant donné une suite de polynômes orthogonaux
 , tout polynôme
, tout polynôme 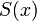 de degré n peut s'exprimer de manière unique comme une combinaison linéaire de
de degré n peut s'exprimer de manière unique comme une combinaison linéaire de 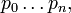 c'est-à-dire qu'il existe des coefficients
c'est-à-dire qu'il existe des coefficients  tel que
tel queLemme 2: Étant donnée une suite de polynômes orthogonaux, tout élément de cette suite est orthogonal à n'importe quel polynôme de degré strictement inférieur.
Ces deux résultats sont des cas particuliers de la théorie des bases dans un espace de Hilbert
Relation de récurrence
Pour toute suite de polynômes orthogonaux (il suffit d'ailleurs que le polynôme pn soit de degré n), il existe une relation de récurrence relativement à trois polynômes consécutifs.
Les coefficients a, b, et c dépendent de n (et aussi de la standardisation).
Démonstration
Le polynôme xpn étant de degré n + 1, on peut l'exprimer sous forme d'une combinaison linéaire des éléments de la base
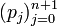 :
:Pour conclure, il reste à utiliser une autre propriété remarquable de notre suite de polynômes: chaque pn est orthogonal à l'espace vectoriel des polynômes de degré inférieur à n. Par conséquent, dès que le degré de xpj est inférieur à n, le coefficient
 est nul. La somme se limite ainsi à une somme à trois termes
est nul. La somme se limite ainsi à une somme à trois termesEn réordonnant ces termes on obtient le résultats annoncé.
Les valeurs de an, bn et cn peuvent être calculées directement. Soient kj et kj' les deux premiers coefficients de pj:et hj le produit scalaire de pj par lui-même :
On obtient
Existence de racines réelles
Tout polynôme d'une suite de polynômes orthogonaux dont le degré n est supérieur ou égal à 1 admet n racines distinctes, toutes réelles, et situées strictement à l'intérieur de l'intervalle d'intégration (c'est une propriété remarquable : il est rare, pour un polynôme de degré élevé dont les coefficients ont été choisis au hasard, d'avoir toutes ses racines réelles)
DémonstrationSoit m le nombre des points où Pn change de signe à l'intérieur de l'intervalle d'intégration ; notons
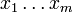 ces points. Ce sont tous des racines de Pn. D'après le théorème fondamental de l'algèbre, m ≤ n. On va montrer m = n. Soit
ces points. Ce sont tous des racines de Pn. D'après le théorème fondamental de l'algèbre, m ≤ n. On va montrer m = n. Soit 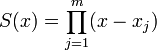 ; c'est un polynôme de degré m qui change de signe en chaque point xj ; S(x)Pn(x) est donc strictement positif, ou strictement négatif, partout sur l'intervalle d'intégration sauf aux points xj , et il en est donc de même de S(x)Pn(x)W(x). Ainsi,
; c'est un polynôme de degré m qui change de signe en chaque point xj ; S(x)Pn(x) est donc strictement positif, ou strictement négatif, partout sur l'intervalle d'intégration sauf aux points xj , et il en est donc de même de S(x)Pn(x)W(x). Ainsi, 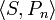 , l'intégrale de ce produit, est non nul. Mais, d'après le Lemme 2, Pn est orthogonal à tous les polynômes de degré inférieur, donc le degré de S doit être n.
, l'intégrale de ce produit, est non nul. Mais, d'après le Lemme 2, Pn est orthogonal à tous les polynômes de degré inférieur, donc le degré de S doit être n.Position des racines
Les racines des polynômes se trouvent strictement entre les racines du polynôme de degré supérieur dans la suite.
DémonstrationOn met d'abord tous les polynômes sous une forme standardisée telle que le coefficient dominant soit positif (ce qui ne change pas les racines). Montrons ensuite le lemme suivant : pour tout n et tout x,
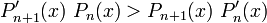 .
.
Démonstration par récurrence. Pour n = 0,
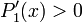 ,
, 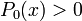 , et
, et 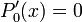 .
.On a la relation de récurrence
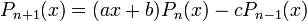 , avec
, avec 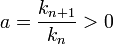 et
et 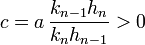 .
.
Donc
et
Mais
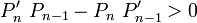 (d'après l'hypothèse de récurrence). Soit alors x une racine de Pn+1, le lemme nous dit que
(d'après l'hypothèse de récurrence). Soit alors x une racine de Pn+1, le lemme nous dit que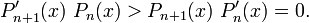 .
.
Ainsi,
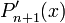 et
et 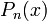 ont le même signe. Mais
ont le même signe. Mais 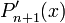 doit changer de signe entre chaque racine de Pn+1 et la suivante. Par conséquent, Pn doit également changer de signe, donc Pn doit avoir une racine dans cet intervalle.
doit changer de signe entre chaque racine de Pn+1 et la suivante. Par conséquent, Pn doit également changer de signe, donc Pn doit avoir une racine dans cet intervalle.Équations différentielles conduisant à des polynômes orthogonaux
Une importante classe des polynômes orthogonaux provient d'une équation différentielle de la forme
où Q est un polynôme quadratique donné et L un polynôme linéaire donné. La fonction f est inconnue, et la constante λ est un paramètre. On peut remarquer qu'une solution polynomiale est a priori envisageable pour une telle équation, les degrés des termes étant compatibles. Cependant, les solutions de cette équation différentielle ont des singularités, à moins que λ ne prenne des valeurs spécifiques. La suite de ces valeurs
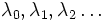 conduit à une suite de polynômes solutions
conduit à une suite de polynômes solutions 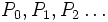 si l'une des assertions suivantes est vérifiée :
si l'une des assertions suivantes est vérifiée :- Q est vraiment quadratique, L est linéaire, Q a deux racines réelles distinctes, la racine de L est située entre les deux racines de Q, et les termes de plus haut degré de Q et L ont le même signe.
- Q n'est pas quadratique, mais linéaire, L est linéaire, les racines de Q et L sont différentes, et les termes de plus haut degré de Q et L ont le même signe si la racine de L est plus petite que celle de Q, ou inversement.
- Q est un polynôme constant non nul, L est linéaire, et le terme de plus haut degré de L est de signe opposé à celui de Q.
Ces trois cas conduisent respectivement aux polynômes de Jacobi, de Laguerre et d'Hermite. Pour chacun de ces cas :
- La solution est une suite de polynômes
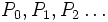 , chaque
, chaque 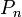 ayant un degré n, et correspondant au nombre
ayant un degré n, et correspondant au nombre 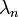 .
. - L'intervalle d'orthogonalité est limité par les racines de Q.
- La racine de L est à l'intérieur de l'intervalle d'orthogonalité.
- En notant
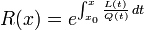 , les polynômes sont orthogonaux sous la fonction poids
, les polynômes sont orthogonaux sous la fonction poids 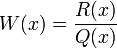
- W(x) ne peut pas s'annuler ou prendre une valeur infinie dans l'intervalle, bien qu'il puisse le faire aux extrémités.
- W(x) peut être choisi positif sur l'intervalle (multiplier l'équation différentielle par -1 si nécessaire)
En raison de la constante d'intégration, la quantité R(x) est définie à une constante multiplicative près. Le tableau ci-dessous donne les valeurs "officielles" de R(x) et W(x).
Formule de Rodrigues
Avec les hypothèses de la section précédente, Pn(x) est proportionnel à
![\frac{1}{W(x)} \ \frac{d^n}{dx^n}\left(W(x)[Q(x)]^n\right)](/pictures/frwiki/51/3918d0b9536540fbeecf695a34d5b28f.png)
équation mieux connue sous le nom de « formule de Rodrigues ». Elle est souvent écrite :
où les nombres en dépendent de la normalisation. Les valeurs de en sont données dans le tableau plus bas.
Les nombres λn
Avec les hypothèses de la section précédente,
(on remarquera que Q étant quadratique et L linéaire, Q'' et L' sont bien des constantes.)
Seconde forme de l'équation différentielle
Avec
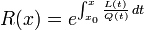 .
.Alors
En multipliant maintenant l'équation différentielle
par R/Q, on obtient
ou encore
C'est la forme normalisée de Sturm-Liouville de l'équation.
Troisième forme de l'équation différentielle
En posant
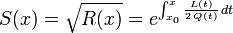 .
.Alors :
En multipliant maintenant l'équation différentielle
par S/Q, on obtient :
ou encore
Mais
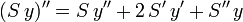 , donc
, doncou, en posant u = Sy,
Tableau des polynômes orthogonaux classiques
Nom et symbole conventionnel Tchebychev, 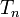
Tchebychev
(seconde sorte),
Legendre, 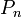
Hermite, 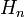
Limite d'orthogonalité 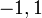
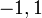
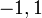
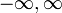
Poids, 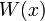
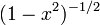
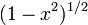
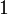
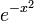
Normalisation 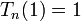
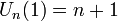
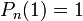
Terme de plus haut degré = 
Carré de la norme 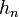
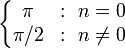
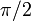
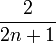
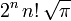
Terme de plus haut degré, 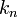
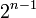

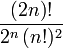

Second terme, 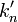
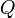
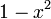
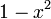
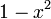
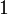
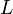
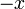
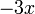
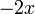
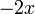
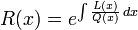
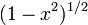
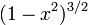
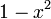
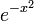
Constante dans l'équation différentielle, 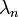
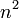
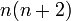


Constante dans la formule de Rodrigues, 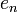
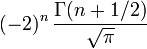
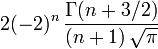
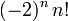
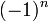
Relation de récurrence, 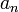
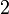
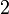
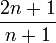
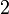
Relation de récurrence, 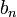
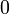
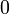
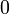
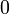
Relation de récurrence, 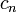
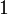
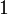
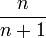

Nom et symbole Laguerre associé, 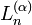
Laguerre, 
Limites d'orthogonalité 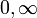
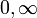
Poids, 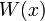

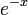
Normalisation Lead term = 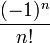
Lead term = 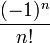
Carré de la norme 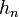
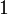
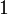
Terme de plus haut degré 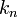
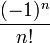
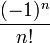
Second terme, 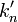
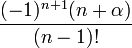
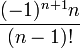
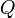
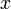
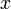
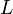
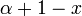
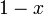
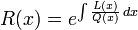
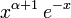
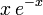
Constante dans l'équation différentielle, 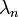
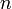
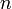
Constante dans la relation de Rodrigues, 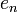
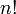
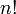
Relation de récurrence, 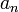
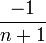
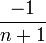
Relation de récurrence, 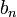
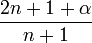
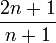
Relation de récurrence, 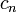

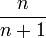
Nom et symbole Gegenbauer, 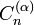
Jacobi, 
Limites d'orthogonalité 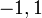
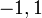
Poids, 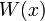
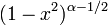
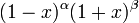
Normalisation 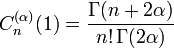 if
if 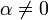
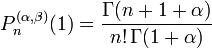
Carré de la norme, 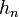
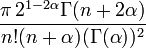

Terme de plus haut degré, 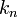
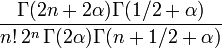
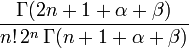
Second terme, 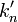
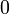
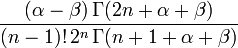
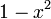
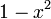
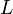
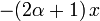
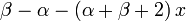
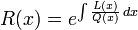
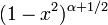
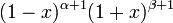
Constante dans l'équation différentielle, 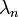

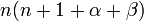
Constante dans l'équation de Rodrigues, 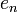
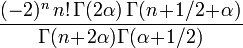
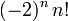
Relation de récurrence, 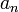
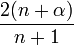
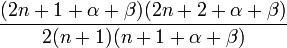
Relation de récurrence, 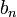
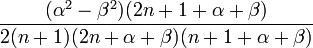
Relation de récurrence, 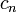
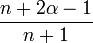
Voir aussi
Références
- Polynômes de Tchebychev sur Math-Linux.
- Portail des mathématiques
Catégories : Algèbre bilinéaire | Espace de Hilbert | Polynôme remarquable
Wikimedia Foundation. 2010.

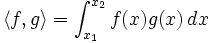
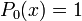
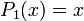
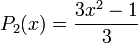
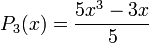
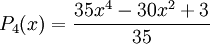

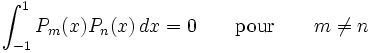

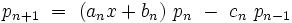
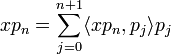

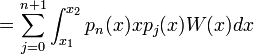
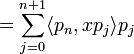


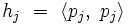
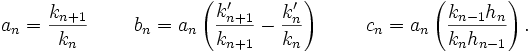
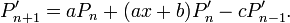
![\begin{align}
& {} \quad P_{n+1}'\ P_n - P_{n+1}\ P_n' = [a P_n + (ax + b) P_n' - c P_{n-1}'] P_n - [(ax + b) P_n - c P_{n-1}] P_n' \\
& {} = [a P_n - c P_{n-1}'] P_n + c P_{n-1}\ P_n' \\
& {} = a P_n^{ 2} + c (P_n'\ P_{n-1} - P_n\ P_{n-1}') \\
& {} \ge c (P_n'\ P_{n-1} - P_n\ P_{n-1}')
\end{align}](/pictures/frwiki/101/ec555f7af0c3a34d8ca0dc6fa930d65b.png)
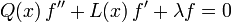
![P_n(x) = \frac{1}{{e_n}W(x)} \ \frac{d^n}{dx^n}\left(W(x)[Q(x)]^n\right)](/pictures/frwiki/48/053c6bdce2a23cedd8699f20a10268e3.png)