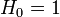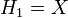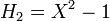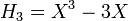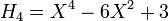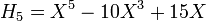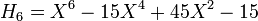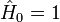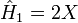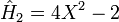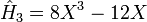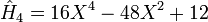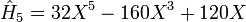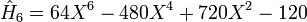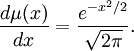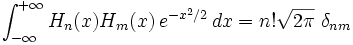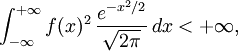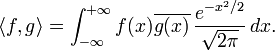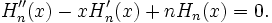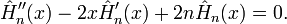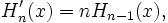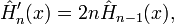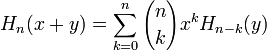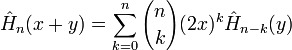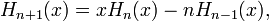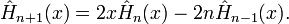Polynome d'Hermite

Polynôme d'Hermite

En mathématiques, les polynômes d'Hermite sont une suite de polynômes qui a été nommée ainsi en l'honneur de Charles Hermite (bien qu'ils aient été surtout étudiés par Joseph-Louis Lagrange lors de ses travaux sur les probabilités). Ils sont définis comme suit :

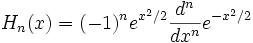$H_n(x)=(-1)^n e^{x^2/2}\frac{d^n}{dx^n}e^{-x^2/2}$ (forme dite probabiliste)

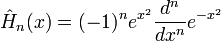$\hat H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}e^{-x^2}$ (forme dite physique)

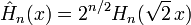Les deux définitions sont liées par la propriété d'échelle suivante: $\hat H_n(x) = 2^{n/2}H_n(\sqrt{2}\,x)\,\!$ .

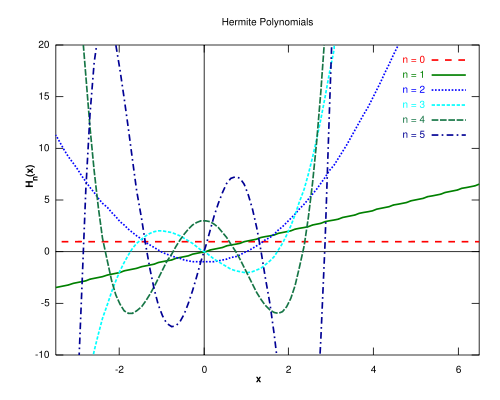
Les premiers polynômes d'Hermite sont les suivants :

$H_0=1~$

$H_1=X~$

$H_2=X^2-1~$

$H_3=X^3-3X~$

$H_4=X^4-6X^2+3~$

$H_5=X^5-10X^3+15X~$

$H_6=X^6-15X^4+45X^2-15~$

$\hat H_0=1~$

$\hat H_1=2X~$

$\hat H_2=4X^2-2~$

$\hat H_3=8X^3-12X~$

$\hat H_4=16X^4-48X^2+12~$

$\hat H_5=32X^5-160X^3+120X~$

$\hat H_6=64X^6-480X^4+720X^2-120~$

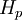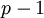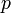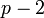On peut démontrer que dans ${H_p}~$ les coefficients d'ordre ayant la même parité que $p-1~$ sont nuls et que les coefficients d'ordre $p~$ et $p-2~$ valent respectivement 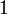$1~$ et $-p(p-1)/2~$ .

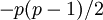Orthogonalité

$H n$ est un polynôme de degré $n$ . Ces polynômes sont orthogonaux pour la mesure $μ$ de densité

$\frac{d\mu(x)}{dx} = \frac{e^{-x^2/2}}{\sqrt{2\pi}}.$

Ils vérifient :

$\int_{-\infty}^{+\infty} H_n(x)H_m(x)\,e^{-x^2/2}\,dx=n!\sqrt{2\pi}~\delta_{nm}$

où $δ n m$ est le symbole de Kronecker. Ces fonctions forment donc une base orthogonale de l'espace de Hilbert 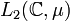$L_2(\mathbb C,\mu)$ des fonctions boréliennes telles que:

$\int_{-\infty}^{+\infty}f(x)^2\,\frac{e^{-x^2/2}}{\sqrt{2\pi}}\,dx< +\infty,$

dans lequel le produit scalaire est donné par l'intégrale

$\langle f,g\rangle=\int_{-\infty}^{+\infty} f(x)\overline{g(x)}\,\frac{e^{-x^2/2}}{\sqrt{2\pi}}\,dx.$

Des propriétés analogues sont vérifiables pour les polynômes de Hermite sous leur forme physique.

Diverses propriétés

Le $n$ -ième polynôme d'Hermite satisfait l'équation différentielle suivante (dans ses deux versions probabiliste ou physique):

$H_n''(x)-xH_n'(x)+nH_n(x)=0.\,$

$\hat H_n''(x)-2x\hat H_n'(x)+2n\hat H_n(x)=0.\,$

Les polynômes satisfont la propriété

$H_n'(x)=nH_{n-1}(x),\,$

$\hat H_n'(x) = 2n \hat H_{n-1}(x),\,$

que l'on peut écrire ainsi

$H_n(x+y)=\sum_{k=0}^n{n \choose k}x^k H_{n-k}(y)$

$\hat H_n(x+y)=\sum_{k=0}^n{n \choose k}(2x)^k \hat H_{n-k}(y)$

Ils vérifient donc la relation de récurrence suivante :

$H_{n+1}(x)= xH_{n}(x) - nH_{n-1}(x),\,$

$\hat H_{n+1}(x)= 2x\hat H_{n}(x) - 2n\hat H_{n-1}(x).\,$

Portail des mathématiques

Ce document provient de « Polyn%C3%B4me d%27Hermite ».

Catégories : Fonction hypergéométrique | Polynôme remarquable | Fonctions spéciales

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Polynome d'Hermite de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Polynôme d'Hermite — En mathématiques, les polynômes d Hermite sont une suite de polynômes qui a été nommée ainsi en l honneur de Charles Hermite (bien qu ils aient été surtout étudiés par Joseph Louis Lagrange lors de ses travaux sur les probabilités). Ils sont… … Wikipédia en Français
polynôme d’Hermite — Ermito daugianaris statusas T sritis fizika atitikmenys: angl. Hermite polynomial vok. Hermitesches Polynom, n rus. полином Эрмита, m; эрмитов полином, m pranc. polynôme d’Hermite, m … Fizikos terminų žodynas
Hermite polynomial — Ermito daugianaris statusas T sritis fizika atitikmenys: angl. Hermite polynomial vok. Hermitesches Polynom, n rus. полином Эрмита, m; эрмитов полином, m pranc. polynôme d’Hermite, m … Fizikos terminų žodynas
Polynome de Laguerre — Polynôme de Laguerre En mathématiques, les polynômes de Laguerre, nommés d après Edmond Laguerre (1834 1886), sont les solutions de l équation de Laguerre : qui est une équation différentielle linéaire du second ordre. Cette équation a des… … Wikipédia en Français
Polynôme de laguerre — En mathématiques, les polynômes de Laguerre, nommés d après Edmond Laguerre (1834 1886), sont les solutions de l équation de Laguerre : qui est une équation différentielle linéaire du second ordre. Cette équation a des solutions non… … Wikipédia en Français
HERMITE (C.) — Les travaux du mathématicien français Charles Hermite portent surtout sur l’algèbre, la théorie des nombres et l’analyse. On lui doit de très nombreux résultats sur la théorie des invariants et sur les fonctions elliptiques et abéliennes, et il… … Encyclopédie Universelle
Polynome de Legendre — Polynôme de Legendre Polynômes de Legendre Les polynômes de Legendre sont des solutions y de l équation différentielle de Legendre. Sommaire 1 … Wikipédia en Français
Polynôme de legendre — Polynômes de Legendre Les polynômes de Legendre sont des solutions y de l équation différentielle de Legendre. Sommaire 1 … Wikipédia en Français
Hermite-Polynom — Die hermiteschen Polynome (nach Charles Hermite) sind Polynome mit folgenden äquivalenten Darstellungen: bzw. Inhaltsverzeichnis … Deutsch Wikipedia
Polynômes d'Hermite — Polynôme d Hermite En mathématiques, les polynômes d Hermite sont une suite de polynômes qui a été nommée ainsi en l honneur de Charles Hermite (bien qu ils aient été surtout étudiés par Joseph Louis Lagrange lors de ses travaux sur les… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Polynome d'Hermite

Polynôme d'Hermite

Orthogonalité

Diverses propriétés

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Polynome d'Hermite

Polynôme d'Hermite

Orthogonalité

Diverses propriétés

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link