Theoreme de la base incomplete

Theoreme de la base incomplete

Théorème de la base incomplète

Le théorème de la base incomplète énonce que toute famille libre de vecteurs d'un espace vectoriel E peut être complétée pour obtenir une base de E.

Sommaire

Enoncé

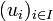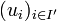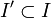Soit E un espace vectoriel, (u_i)_{i \in I} une famille génératrice de E et (u_i)_{i \in I'} avec I'\subset I, une famille libre.

Alors il existe I'' tel que 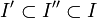I'\subset I''\subset I et tel que 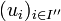(u_i)_{i \in I''} soit une base de E.

Démonstration

Cas où I est fini (et donc E est de dimension finie)

La démonstration dans le cas fini est un simple algorithme :

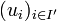
  1. on part de la famille libre initiale (u_i)_{i \in I'}
  2. si cette famille n'est pas génératrice (n'est pas une base), on lui ajoute un élément 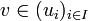v \in (u_i)_{i \in I} tel que v n'est pas une combinaison linéaire de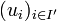 (u_i)_{i \in I'}
  3. on réitère 2 jusqu'à ce que l'on obtienne une base

Preuve de la correction :

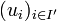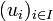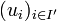  • Premier invariant à démontrer : en 2, si (u_i)_{i \in I'} est bien une famille libre non génératrice, on peut lui adjoindre un élément de (u_i)_{i \in I} qui n'est pas combinaison linéaire de (u_i)_{i \in I'}.
En effet, s'il n'existait pas d'élément de 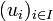(u_i)_{i \in I} qui ne soit pas combinaison linéaire de 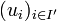(u_i)_{i \in I'}, cela voudrait dire que 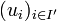(u_i)_{i \in I'} peut générer tout 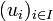(u_i)_{i \in I}, et donc tout E, puisque cette dernière famille est génératrice de E. Donc 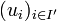(u_i)_{i \in I'} serait déjà génératrice de E.
  • Deuxième invariant à démontrer : lorsque l'on ajoute un tel élément à 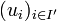(u_i)_{i \in I'}, la nouvelle famille obtenue est toujours libre.
En effet, le nouvel élément n'est pas une combinaison linéaire des précédents.

Preuve de la terminaison :

À chaque itération, on augmente 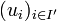(u_i)_{i \in I'} d'un élément de 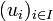(u_i)_{i \in I} à chaque fois différent (en effet, on ne peut pas prendre deux fois un élément car il est combinaison linéaire de lui-même). Or 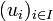(u_i)_{i \in I} est fini, donc l'algorithme doit s'arrêter au bout d'un nombre fini d'étapes.

Il découle de cela que l'algorithme s'arrêtera dans un temps fini et que lorsqu'il s'arrête, il a forcément exhibé une famille génératrice et libre de E, c'est-à-dire une base.

Cas général

La démonstration dans le cas général fait intervenir le Lemme de Zorn, et donc indirectement, l'axiome du choix. Elle est due au mathématicien Georg Hamel.

En effet, on doit considérer l'ensemble des familles libres incluses dans 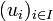(u_i)_{i \in I} et remarquer qu'elles forment un ensemble inductif pour l'inclusion. Le lemme de Zorn assure donc qu'il existe une famille maximale, et on constate que cette famille maximale est justement une base de E.

Corollaire

Tout espace vectoriel admet une base.

Il suffit en effet d'appliquer le théorème de la base incomplète avec I' vide (famille libre) et I égal à l'espace vectoriel (famille génératrice) pour obtenir ce résultat.

Corollaire

Soit E un K-espace vectoriel et F un sous-espace vectoriel de E Alors F possède un supplémentaire dans E, i.e. il existe un sous-espace vectoriel G de E tel que 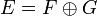E=F \oplus G. En effet, c'est clair si F={0} ou F=E; sinon, on considère une base B de F qu'on complète en une base B' de E: l'espace engendré par les vecteurs de B' qui ne sont pas dans F convient.

Une conséquence contre-intuitive

Munissons \mathbb{R} de sa structure naturelle de \mathbb{Q}-espace vectoriel. Si on suppose l'axiome du choix, \mathbb{Q} possède un supplémentaire G dans \mathbb{R}. G est alors un sous-groupe additif strict indénombrable et non Lebesgue-mesurable de \mathbb{R}; de plus, il ne contient aucun rationnel non nul. Si f est la symétrie par rapport à \mathbb{Q} parallèlement à G, f est une involution de \mathbb{R} continue nulle part, non mesurable, de graphe dense et fixant chaque rationnel. Ce type de construction est typique de l'utilisation de l'axiome du choix. On pourra lire dans le même esprit une construction, avec axiome du choix, d'automorphismes de corps non continus de C.

Voir aussi

Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs Colinéarité • Indépendance linéaire • Famille libre • Rang • Famille génératrice • Base • Théorème de la base incomplète Mathématiques
Sous-espace Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension d'un espace vectoriel • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Endomorphisme nilpotent
En dimension finie Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford
Enrichissements de structure Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de la base incompl%C3%A8te ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de la base incomplete de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Théorème de la base incomplète — En algèbre linéaire, le théorème de la base incomplète affirme que, dans un espace vectoriel E, toute famille libre de vecteurs peut être complétée en une famille libre et génératrice de E (c est à dire une base de E) ; de toute famille… …   Wikipédia en Français

  • Base (Algèbre Linéaire) — Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse être exprimé de manière… …   Wikipédia en Français

  • Base (algebre lineaire) — Base (algèbre linéaire) Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse… …   Wikipédia en Français

  • Base d'un espace — Base (algèbre linéaire) Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse… …   Wikipédia en Français

  • Base vectorielle — Base (algèbre linéaire) Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse… …   Wikipédia en Français

  • Theoreme d'Artin-Wedderburn — Théorème d Artin Wedderburn En mathématiques et plus particulièrement en algèbre le Théorème d Artin Wedderburn traite de la structure d algèbre ou d anneau semi simple. Il correspond au théorème fondamental des structures semi simples et permet… …   Wikipédia en Français

  • Théorème d'artin-wedderburn — En mathématiques et plus particulièrement en algèbre le Théorème d Artin Wedderburn traite de la structure d algèbre ou d anneau semi simple. Il correspond au théorème fondamental des structures semi simples et permet d expliciter exactement leur …   Wikipédia en Français

  • Theoreme de Cayley-Hamilton — Théorème de Cayley Hamilton Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace… …   Wikipédia en Français

  • Théorème de Hamilton-Cayley — Théorème de Cayley Hamilton Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace… …   Wikipédia en Français

  • Théorème de cayley-hamilton — Pour les articles homonymes, voir Hamilton. En algèbre linéaire, le théorème de Cayley Hamilton (qui porte les noms des mathématiciens Arthur Cayley et William Hamilton) affirme que tout endomorphisme d un espace vectoriel de dimension finie sur… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”