- Astronomie arabe
-
Dans l’histoire de l'astronomie, l’astronomie arabe renvoie aux découvertes astronomiques accomplies par la civilisation islamique, particulièrement au cours de l’Âge d'or de l'Islam (VIIIe siècle-XVIe siècle), et transcrites pour la plupart en langue arabe. Ces découvertes ont été effectuées pour l’essentiel dans les sultanats du Moyen-Orient, d’Asie centrale, dans l’Al-Andalus, en Afrique du Nord, puis plus tard en Chine et en Inde. Les débuts de l’astronomie ont procédé d'un cheminement semblable aux autres sciences dans l’Islam, par l’assimilation de connaissances de l’étranger et la composition de ces éléments disparates pour faire naître une tradition originale. Les principaux apports sont indiens, perses et grecs, connus par des traductions puis assimilés[1]. Par la suite, l’astronomie arabe exercera à son tour une influence significative sur les astronomies indienne[2] et européenne[3] et même sur l’astronomie chinoise[4].
Plusieurs étoiles visibles à l’œil nu dans le ciel, comme Aldébaran (α Tauri) et Altaïr (α Aquilae), ainsi que plusieurs termes d’astronomie comme « alidade », « azimut » et « almucantarat » témoignent par leur morphologie de leur origine arabe[5].
Avec environ 10 000 manuscrits conservés à travers le monde, dont une grande partie n’a toujours pas fait l’objet d'un inventaire bibliographique, le corpus astronomique arabe constitue l’une des composantes les mieux préservées de la littérature scientifique médiévale. Malgré les lacunes bibliographiques, les textes étudiés à ce jour fournissent une image fidèle de l’activité astronomique des peuples de langue arabe[6].
Sommaire
- 1 L’islam et l’astronomie
- 2 Histoire
- 3 Observatoires
- 4 Instruments
- 5 Traités célèbres
- 6 Noms d'étoiles d'origine arabe
- 7 Notes et références
- 8 Voir aussi
L’islam et l’astronomie
L’islam a influencé l'astronomie de manière à la fois directe et indirecte. La discipline religieuse, en posant un certain nombre de problèmes liés au calendrier, a donné un élan décisif à l'épanouissement de l’astronomie mathématique, et notamment à la trigonométrie sphérique[1].
Contexte
Au VIIe siècle, chrétiens et Juifs pratiquaient des cérémonies religieuses liées au cycle des saisons, mais dont la date était déterminée par les phases de la lune, comme Pâques et Pessa'h. Ces deux religions étaient confrontées au fait que le mois lunaire, d’une durée d’environ 29,5 jours, n’est pas une division exacte de l’année tropique de 365 jours. Pour résoudre cette difficulté, les chrétiens avaient séparé le calendrier civil et le calendrier des fêtes "mobiles" ; quant aux Juifs, ils avaient adopté un calendrier fondé sur une découverte remontant à -430 par l’athénien Méton. Dans l'intervalle du cycle métonique, qui dure 19 ans, on dénombre 12 années de 12 mois lunaires et sept années de 13 mois lunaires. Ainsi, par interposition périodique d'un mois intercalaire, le calendrier annuel hébreu suivait à peu près le cycle des saisons[1].
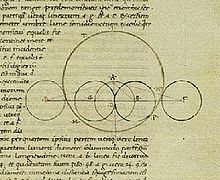
Les astronomes, quant à eux, exploitaient le modèle de Ptolémée pour déterminer les positions de la lune et des étoiles. La méthode utilisée par Ptolémée pour résoudre les triangles sphériques, imaginée par Ménélaos d'Alexandrie à la fin du Ier siècle, était encore maladroite : elle procédait par intersection de deux triangles rectangles ; une application du théorème de Ménélaüs permettait ainsi de trouver un arc inconnu pourvu qu'on connaisse les cinq autres éléments du triangle sphérique. Par exemple, pour déterminer l'heure à partir de l’altitude du Soleil, il fallait plusieurs applications successives du théorème de Ménélaüs. Ainsi, pour les astronomes arabes du Moyen Âge, la recherche d'une méthode trigonométrique plus simple constituait un défi très naturel[1].
Le Coran et l’astronomie
L’islam encourage les musulmans à rechercher leur chemin grâce aux astres. Le Coran énonce en effet : « C'est lui qui a placé pour vous les étoiles (dans le ciel) afin que vous soyez dirigés dans les ténèbres sur la terre et sur les mers[7]. » Avec une telle incitation, les premiers musulmans ne tardèrent pas à perfectionner les instruments astronomiques et de navigation, d'où vient qu'aujourd'hui encore, la plupart des étoiles naguère utilisées par les marins portent des noms arabes[1].
Le Coran influa également sur l'astronomie arabe « par son enseignement selon lequel l’Univers est réglé selon une loi fondamentale » qui « plonge ses racines dans le concept islamique du tawhîd, l’unité de Dieu », ainsi que par « la place plus importante qu'il accorde aux données empiriques que ne le faisaient la civilisation hellène » qui poussa les musulmans à « s'investir davantage dans l’observation du ciel que ne l’avaient fait les penseurs grecs, notamment les platoniciens et les aristotéliciens[8] », lesquels se défiaient des représentations des sens et estimaient que la raison suffit pour comprendre la Nature. L’accent mis par le Coran sur l’importance de l’observation, de l’interprétation et de la contemplation (par la récurrence des verbes « voir », « méditer » et « contempler »), poussèrent ainsi les musulmans à concevoir une méthode scientifique originale accordant une place particulière aux faits d’observation. Muhammad Iqbal écrit à ce sujet[9] :
« Le ton généralement empiriste du Coran suscita chez ses lecteurs le respect des faits, et devait faire d'eux les pionniers de la science moderne. Ce n'était pas un mince progrès que d'éveiller l'empirisme à une époque qui se détournait du visible comme dépourvu de valeur pour l’homme dans sa quête du Divin. »
On trouve d’ailleurs plusieurs versets cosmologiques dans le Coran (610-632), où l'on retrouve le schéma antique de séparation de la terre et des cieux, conçus initialement comme deux surfaces accolées :
- « Les infidèles ne voient-ils pas que les cieux et la terre formaient une masse compacte, et que nous les avons séparés[10] ? »
- « Nous avons bâti le ciel de nos mains et nous l’avons étendu dans l’espace[11]. »
Un autre verset évoque le modèle cosmographique grec :
- « Ne voyez-vous pas comment Dieu a créé les sept cieux, disposés par couches, s'enveloppant les unes les autres[12]. »
Divers hadiths attribués à Mahomet témoignent aussi qu'il s'est opposé à l’astrologie et aux superstitions en général. Par exemple, lorsqu'une éclipse survint à la mort de son fils Ibrahim ibn Muhammad, et qu'une rumeur interprétait ce phénomène comme un signe de la compassion de Dieu, Mahomet aurait affirmé[13] :
« Une éclipse est un phénomène naturel. C'est folie d’attribuer de telles choses à la mort ou à la naissance d'un homme[réf. souhaitée]. »
Pratiques islamiques
Plusieurs règles de l’islam ont poussé les fidèles à améliorer calculs et observations astronomiques.
Le premier motif est le calendrier musulman. Le Coran édicte en effet que « Le nombre des mois est de douze devant Dieu, tel il est dans le livre de Dieu, depuis le jour où il créa les cieux et la terre. Quatre de ces mois sont sacrés ; c’est la croyance constante[14],[1]. » Pour cette raison, les musulmans ne pouvaient se contenter ni du calendrier chrétien ni du calendrier hébreu, et devaient en créer un nouveau.
Le second motif est l'interprétation du mouvement lunaire. Les mois, dans la religion musulmane, ne commencent pas avec la nouvelle lune astronomique, définie comme l'instant où la lune a la même longitude écliptique que le soleil (elle est donc invisible, noyée dans l'albédo solaire) ; les mois commencent lorsque le croissant lunaire commence à apparaître au crépuscule[1]. Le Coran dit précisément : « Ils t’interrogeront sur les nouvelles lunes. Dis-leur : Ce sont les époques fixées pour l’utilité de tous les hommes et pour marquer le pèlerinage de la Mecque[15],[16]. » Pour déterminer les phases de la lune, il fallut développer de nouvelles méthodes de calcul et mettre aux points des instruments adaptés à l'observation de la lune[17].
Les musulmans sont également tenus de prier en se prosternant dans la direction de la Kaaba à La Mecque et d’orienter leurs mosquées dans cette direction : il leur faut donc aussi savoir trouver la direction de cet endroit, où qu'ils se trouvent sur Terre[18],[19]. Le dernier problème est la détermination du moment de la Salah. Les musulmans doivent pouvoir déterminer les heures de prière à cinq moments de la journée (de l’aurore au soir) à partir de la position des astres[1],[20].
Recours à la géométrie sphérique
Article détaillé : Mathématiques arabes.Le calcul du jour où le croissant lunaire recommence à devenir visible constituait un redoutable défi pour les savants arabes. Bien qu'en effet la théorie de Ptolémée du mouvement composé de la lune soit assez exacte à l'époque de la nouvelle lune, elle ne donne la trajectoire de la lune que par rapport au cercle de l’écliptique. Pour prédire quel jour la lune commence à redevenir visible, il fallait pouvoir décrire son mouvement par rapport à l’horizon, un problème dont la résolution appartient à une géométrie sphérique assez sophistiquée. Ce sont la détermination de la direction de la Mecque depuis un lieu donné et l'heure des Salah qui ont poussé les musulmans à élaborer une telle géométrie. La résolution de ces problèmes suppose en effet que l'on sache calculer le côté d'un triangle sphérique de la sphère céleste à partir de ses trois angles et des deux autres côtés ; pour trouver l'heure sidérale, par exemple, il faut savoir construire le triangle dont les sommets sont le zénith, le pôle nord, et la position du Soleil. L’observateur doit connaître l’ascension droite du Soleil et celle du pôle : la première peut être mesurée au sextant, et la seconde n'est autre que la latitude de l’observateur. L'heure est donnée par l’angle entre le méridien (l’arc compris entre le zénith et le pôle) et le cercle horaire du Soleil (c’est-à-dire l’arc compris entre le Soleil et le pôle)[1],[20].
Histoire
La connaissance du ciel dans l’Arabie prémusulmane n’était qu’empirique : elle se limitait au lever et au coucher des astres. On considère généralement que l'essor de l'islam a provoqué un renouveau de la pensée des Arabes dans ce domaine[21]. Les débuts de l’astronomie ont procédé d'un cheminement semblables aux autres sciences dans l’islam, par l’assimilation de connaissances de l’étranger et la composition de ces éléments disparates pour faire naître une tradition originale. Les principaux apports sont indiens, perses et grecs, connus par des traductions et commentés.
L’historien des sciences Donald R. Hill divise l'astronomie arabe en quatre périodes[21] :
- Assimilation par syncrétisme des doctrines astronomiques hellénistiques, indiennes et perses (700—825)
- Phase de recherche intense, réception et amélioration du système de Ptolémée (825—1025)
- Épanouissement d'une école de pensée spécifiquement arabe en astronomie (1025—1450)
- Stagnation, encore ponctuée de quelques contributions remarquables (1450—1900)
Pratiques astronomiques au temps de l'Hégire (610-700)
À ses débuts, la communauté musulmane de Médine observait les dates de la nouvelle lune pour arrêter la durée des mois lunaires, particulièrement en vue de fixer le Ramadan et les fêtes mobiles.
Vers l'an 638, le calife Omar mit en usage un nouveau calendrier lunaire fondé sur l'enseignement de l’islam. Ce calendrier comportait douze mois lunaires, dont le premier jour était déterminé par l'observation du croissant lunaire. L'année résultant de ce calendrier, toujours en usage chez les musulmans[1],[22], est plus courte d'environ onze jours que l'année tropique.
Premiers apports de l’étranger (700-825)
Cette période est essentiellement marquée par une assimilation et un syncrétisme des doctrines astronomiques hellénistiques, indiennes et perses antérieures.
L'impulsion initiale
Les historiens discernent plusieurs facteurs favorables au développement de l'astronomie arabe. Le premier est la proximité des pays musulmans avec le monde de l'Antiquité classique. Un nombre considérable d'écrits grecs, sanskrits et pehlevis furent traduits en arabe dès le IXe siècle. Ce mouvement était possible grâce au respect envers les savants d'autres cultures[1].
Une autre impulsion résulte des pratiques religieuses propres à l'islam, qui recèlent une foule de problèmes d'astronomie mathématique. La résolution de ces problèmes par les savants musulmans est allée bien au-delà des méthodes mathématiques des Grecs[1].
Autorité des Anciens et traductions
À cette époque, on traduisit pour la première fois un grand nombre d'écrits sanskrits et pehlevis en arabe. La plus célèbre de ces traductions est celle du Surya Siddhanta et des livres de Brahmagupta, parue en 777 sous le titre Zij al-Sindhind[23], et due à la plume de Muhammad al-Fazari et de Yaqūb ibn Tāriq. Les sources disponibles révèlent que ce texte fut traduit après la visite d'un astronome indien à la cour du calife Al Mansour en 770. Le plus remarquable livre en pehlevi traduit à cette époque est le Zij al-Shah, un recueil de chroniques astronomiques compilées sur deux siècles dans la Perse des Sassanides.
Des fragments de cette période témoignent de l’adoption par les Arabes des tables de sinus (héritées des mathématiques indiennes) de préférence aux tables des cordes employées par les astronomes grecs[21]. Autre héritage des Indiens, la formule approchée du temps sidéral adoptée par les astronomes arabes[24].
L’intérêt des Arabes pour l’astronomie a cru parallèlement à celui pour les mathématiques. De ce point de vue, le rôle joué par l’Almageste (composé vers l’an 150) de l’astronome alexandrin Ptolémée (vers 100 - 178) est exemplaire. L’Almageste a effectivement fait date en astronomie, rassemblant, à l’instar des Éléments d’Euclide pour la géométrie, toutes les connaissances contemporaines de leur auteur. Cet ouvrage, dont le titre original est La composition mathématique, acquit au fil des siècles le titre d'usage de Grande Astronomie[25]. Les Arabes l’intitulèrent à leur tour Le Très Grand, ajoutant au superlatif grec megiste (« Très Grand ») l’article défini arabe al- : ainsi l’ouvrage a-t-il été transmis à l’Occident latin sous le titre d’Almageste[26]. Bien que l’essentiel de l’enseignement de l’Almageste, et même de ses hypothèses, devînt de plus en plus anachronique au fil du progrès des observations, il demeura un des piliers de l'enseignement de l’astronomie tant dans le monde musulman qu’en Europe jusqu'à la révolution de Maragha et à la Révolution copernicienne[27]. Ptolémée avait par ailleurs composé d'autres ouvrages, comme une Optique, des Harmoniques, et certains pensent qu’il est aussi l’auteur du Tétrabible, célèbre traité d’astrologie.
L’Almageste constitue véritablement une somme des connaissances des Anciens par les listes exhaustives des phénomènes sidéraux qui y figurent : des tables chronologiques des rois assyriens, perses, grecs, et des empereurs romains, qui permettent de synchroniser les phénomènes astronomiques et les événements historiques. Outre sa pertinence pour dresser des calendriers précis, il rapprochait les connaissances de civilisations très différentes et très éloignées les unes des autres par leur intérêt partagé pour le ciel et l’astrologie. L'ouvrage de Ptolémée devait être recopié et commenté décennie après décennie par les astronomes et les astrologues Arabes, Perses et autres de confession musulmane.
Triomphe du système de Ptolémée (825-1025)
La période qui s'étend du IXe siècle au début du XIe siècle fut marquée par d'intenses recherches, à la suite desquelles on reconnut d'abord la supériorité du système de Ptolémée sur les autres, et où on lui apporta diverses précisions. La recherche astronomique étant vivement encouragée par le calife abbasside al-Ma’mūn, Bagdad et Damas devinrent des centres scientifiques majeurs. Non seulement les califes apportaient à ces travaux un soutien financier, mais ils conféraient aux savants un réel prestige[28].
Astronomie d'observation
 Muhammad Al-Khwarizmi, père de l’algèbre, composa le Zij al-Sindh, l’une des premières tables astronomiques en langue arabe.
Muhammad Al-Khwarizmi, père de l’algèbre, composa le Zij al-Sindh, l’une des premières tables astronomiques en langue arabe.
En astronomie d'observation, le premier ouvrage d’astronomie proprement arabe est le Zij al-Sindh d’Al-Khawarizmi (830). Ce livre, un ensemble de tables donnant les positions successives du Soleil, de la lune et des cinq planètes connues à l'époque, a joué un rôle essentiel par l’introduction des concepts indiens et grecs dans les sciences arabes. Il marque également un tournant dans l’astronomie arabe : jusque-là, en effet, les astronomes s’étaient bornés à appliquer les connaissances anciennes, à traduire des ouvrages devenus classiques et à s’assimiler les données d'autrui : le livre d’Al-Khwarizmi au contraire innove à la fois au plan de l'approche des faits et du calcul[29].
En 850, Alfraganus rédigea Kitab fi Jawani (« Abrégé de la science des étoiles »). C’était avant tout un abrégé de la cosmographie de Ptolémée ; toutefois, il corrigeait aussi l'Almageste en s’appuyant sur les observations d’autres astronomes persans. Alfraganus proposa ainsi de nouvelles valeurs pour l’inclinaison de l’écliptique, le mouvement de précession des apogées du soleil et de la lune, et la circonférence de la Terre. Ces livres, qui connurent une large diffusion dans le monde musulman, furent même traduits en latin[30].
Albatenius (853-929) découvrit que la direction de l’excentricité du Soleil était variable, ce qu’en termes modernes on exprime en disant que la Terre décrit une orbite elliptique autour du Soleil[31]. Les périodes de retour de la nouvelle Lune, la durée de l’année tropique et de l’année sidérale, la prédiction des éclipses, et ses travaux sur le phénomène de parallaxe mirent, selon Wickens, les astronomes à portée des concepts modernes de relativité et d’Âge de l'univers[32]. » Son contemporain, Yahya Ibn Abi Mansour, procéda à des observations et des mesures systématiques, qu'il exploita dans son Al-Zij al-Mumtahan, où il corrige entièrement les valeurs données dans l’Almageste[33].
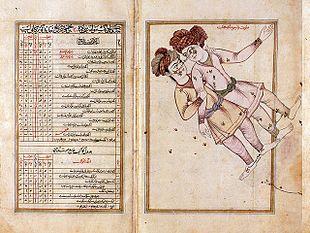 La constellation des Gémeaux d'après le Livre des étoiles fixes d’Al-Soufi, qui décrit en détail environ un millier d'étoiles et donnait les premières descriptions de la Galaxie d'Andromède et du Grand Nuage de Magellan.
La constellation des Gémeaux d'après le Livre des étoiles fixes d’Al-Soufi, qui décrit en détail environ un millier d'étoiles et donnait les premières descriptions de la Galaxie d'Andromède et du Grand Nuage de Magellan.
Au Xe siècle, Al-Soufi décrivit grâce à ses observations la position, la magnitude, la luminosité, et la couleur des étoiles, dessinant les constellations une par une dans son Livre des étoiles fixes (964). Il est aussi le premier à avoir décrit et représenté un « petit nuage » qu’on appelle aujourd’hui la Galaxie d'Andromède : il dit qu'elle se trouve devant la bouche de cette constellation que les Arabes appelaient le « Grand Poisson ». Ce nuage était probablement déjà bien connu des astronomes d’Ispahan, c'est-à-dire dès avant 905 de notre ère[34]. La première mention connue du Grand Nuage de Magellan est également due à Abd Al-Rahman al-Soufi[35],[36].
Ibn Yunus releva méticuleusement année après année plus de 10 000 positions du Soleil en se servant d'un grand astrolabe (d'un diamètre d'environ 1,40 m). Ses observations des éclipses étaient encore utilisées, des siècles plus tard, par Simon Newcomb dans ses recherches sur le mouvement de la Lune, tandis que ses autres observations inspirèrent à Laplace ses remarques sur l’Obliquité de l’Écliptique et sur les Inégalités de Jupiter et de Saturne[37].
Al-Khujandi calcula assez précisément l’angle d’inclinaison de l’écliptique qu'il trouva égale à 23°32'19" (soit en degrés décimaux 23,53°)[38]. En 1006, l’astronome égyptien Ali ibn Ridwan observa SN 1006, la plus brillante supernova de toute l'histoire, et nous a laissé une description détaillée de cet astre éphémère : il dit que cet astre avait deux à trois fois le diamètre apparent de Vénus, à peu près un quart de la luminosité de la Lune, et qu'elle se trouvait bas sur le quadrant sud de l’horizon. On constata par la suite que les moines de l’abbaye bénédictine de Saint-Gall corroboraient les observations de bin Ridwan sur la magnitude et la position dans le ciel de la supernova.
Premiers modèles héliocentriques
À la fin du IXe siècle, Albumasar développa un modèle planétaire que certains ont interprété comme un modèle héliocentrique, par le fait que les révolutions orbitales des planètes s’y font autour du Soleil et non autour de la Terre, et que le seul modèle planétaire où cela advient est le modèle héliocentrique. Cette œuvre n'a pas survécu, mais ses tables astronomiques ont été recopiées ensuite par al-Hashimi, Al-Biruni et al-Sijzi[39].
Au début du XIe siècle, Al-Biruni avait déjà rencontré des savants indiens partisans de l'héliocentrisme. Dans ses Indica, il commente les théories de la rotation de la Terre acceptées par Brahmagupta et d'autres astronomes indiens, tandis que dans son Canon Masudicus, il écrit que les disciples d’Âryabhata assignent à la Terre un premier mouvement d'Est en Ouest, et une second mouvement d'Ouest en est aux étoiles. Al-Biruni rapport également qu'Al-Sijzi est adepte du mouvement de la Terre et qu'il a mis au point un astrolabe appelé "Zouraqi" fondé sur cette hypothèse[40] :
« J’ai vu l’astrolabe appelé Zouraqi inventé par Abu Sa'id Sijzi. Je l’ai admiré et j’en ai fait louange, car il est construit sur une idée avancée par certains, selon laquelle les mouvements que nous voyons sont dus au mouvement de la Terre et non à des mouvements des astres. Sur ma vie, voilà un problème difficile à résoudre et à réfuter. [...] car cela revient au même que de supposer que la Terre est mobile dans le ciel. Dans les deux cas, la connaissance astronomique n'est pas remise en cause. Il n'y a que le physicien qui puisse dire s'il est possible de le réfuter. »
Dans ses Indica, al-Biruni évoque un de ses livres (aujourd'hui perdu) sur la réfutation de l’héliocentrisme, la Clef de l’Astronomie[40] :
« Les plus fameux astronomes anciens et modernes ont soigneusement étudié la question du mouvement de la Terre, et ont essayé de la réfuter. Nous aussi, nous avons consacré un livre à ce sujet intitulé Miftah 'ilm al-hai'ah (Clef de l’Astronomie), et dans lequel nous pensons avoir surpassé nos prédécesseurs, si ce n'est par les mots, du moins par les idées. »
Cosmologie
À la différence des philosophes grecs qui croyaient que l’univers n'avait pas de commencement, les philosophes et les théologiens médiévaux se plaçaient dans le cadre d'une genèse de l’univers. Ce point de vue était celui des trois religions abrahamiques: le judaïsme, le christianisme et l’islam. C'est en l'occurrence un philosophe chrétien, Jean Philopon, qui présenta le premier une objection à la doctrine grecque du passé infini. Toutefois, les arguments les plus sophistiqués sont certainement ceux du philosophe musulman Al-Kindi, du philosophe juif Saadia Gaon (Saadia ben Joseph) et du théologien musulman Algazel. Ils y opposaient deux arguments logiques : le premier tiré de « l’impossibilité de l’existence d'un infini actuel », qui s'énonce[41] :
- « Il ne peut exister un infini actuel. »
- « La régression indéfinie dans le temps des événements est un infini actuel. »
- « .•. Il ne peut exister de régression temporelle indéfinie des événements. »
Le second argument est tiré de « l’impossibilité d'achever un infini actuel par ajouts successifs », s'énonce[41] :
- « Un infini actuel ne peut être achevé par ajouts successifs. »
- « La succession des événements du passé est complétée par ajouts successifs. »
- « .•. La succession des événements du passé ne peut être un infini actuel. »
Ces deux arguments furent adoptés sous une forme ou une autre par des philosophes et des théologiens chrétiens, et le second argument en particulier est devenu célèbre sous la forme que lui a donnée Kant dans sa thèse de la première antinomie concernant le temps[41].
Astronomie expérimentale, astrophysique et mécanique céleste
Au IXe siècle, l’aîné des frères Banou Moussa, Ja'far Muhammad ibn Mūsā ibn Shākir, apporta des contributions décisives à l’astrophysique et à la mécanique céleste. Il fut le premier à formuler l'hypothèse selon laquelle les sphères célestes sont soumises aux mêmes lois physiques que la Terre, alors que les Anciens pensaient que ces sphères étaient régies par des lois distinctes[42]. Dans son traité Du mouvement astral et de La Force d’Attraction, Muhammad ibn Musa proposa aussi l'existence d'une force d’attraction entre corps célestes[43], annonçant la loi de la gravitation universelle[44].
Au Xe siècle, Albatenius (853-929) introduisit l'idée d’éprouver les « observations du passé en en faisant de nouvelles[45]. » Cela incita les astronomes arabes à multiplier les observations empiriques et à développer les techniques expérimentales à partir du XIe siècle[46].
Au début du XIe siècle, Alhazen rédigea un traité intitulé Maqala fi daw al-qamar (Sur l’éclat de la Lune) certainement avant 1021. C'était la première tentative satisfaisante de combiner l'astronomie mathématique et la physique et la première application de la méthode expérimentale en astronomie et en astrophysique. Il démentit l'opinion universellement reçue selon laquelle la Lune réfléchit la lumière du Soleil comme un miroir et conclut qu'elle émet plutôt « de la lumière par les portions de sa surface que la lumière du Soleil frappe. » Pour démontrer que « la lumière est émise depuis chaque point de la surface illuminée de la Lune », il fabriqua un « ingénieux dispositif expérimental ». Alhazen avait « formulée une conception claire des rapports entre un modèle mathématique idéalisé et la complexité des phénomènes observables ; en particulier, il fut le premier à faire varier de façon uniforme et reproductible les conditions expérimentales, dans une expérience montrant que l’intensité de la tache de lumière projetée sur un écran par la clarté lunaire à travers deux petits diaphragmes diminue constamment lorsque l'on referme régulièrement l'un des deux diaphragmes[47]. »
Alhazen, dans son Kitâb fi'l Manazîr (Traité d'optique, composé entre 1015 et 1021), découvrit le premier que les sphères célestes ne sont pas faites de matière solide, et il établit en outre que les cieux sont moins denses que l’air. Ces idées, reprises par Vitellion, eurent une influence décisive sur les systèmes copernicien et tychonien de l’astronomie[48].
Alhazen réfuta aussi les idées d’Aristote sur la nature de la Voie lactée. Aristote croyait qu'elle résultait de « l’ignition d'exhalaisons violentes de nombreuses étoiles de grande taille serrées les unes contre les autres » et que « l’ignition a lieu dans la partie supérieure de l’atmosphère, dans la sphère sublunaire, une région de l'univers qui touche à la sphère céleste des fixes[49]. » Alhazen réfuta cette opinion en entreprenant pour la première fois de mesurer la parallaxe de la Voie lactée[50] et ainsi il put « établir que, puisque la Voie lactée ne présente aucune parallaxe, elle est extrêmement éloignée de la Terre et ne peut donc appartenir à l’atmosphère[51]. »
Toujours au début du XIe siècle, al-Biruni introduisit la méthode expérimentale en astronomie et fut le premier à mener des expériences élaborées à propos des phénomènes astronomiques[52]. Il découvrit que la Voie lactée est un ensemble d'innombrables étoiles nébuleuses[53]. En Afghanistan, il observa et décrivit en détail l’éclipse solaire du 8 avril 1019, et l’éclipse lunaire du 17 septembre 1019, et produisit les latitudes exactes des étoiles pendant l’éclipse lunaire[52].
Critique du ptolémaïsme et nouvelles écoles (1025-1450)
Cette période voit l’éclosion d'une doctrine astronomique proprement musulmane. Dans la tradition grecque et celles qui la suivirent, on distinguait traditionnellement l'astronomie mathématique (dont Ptolémée est un représentant typique) de la cosmologie, branche de la philosophie (représentée par Aristote). Les savants musulmans recherchèrent une configuration physique (hay’a) de l’univers simultanément compatible avec les axiomes mathématiques et les principes physiques. Dans le cadre de cette tradition hay’a, les astronomes musulmans mirent en cause les détails techniques du système de Ptolémée en astronomie[54]. Ces critiques, cependant, préservaient le paradigme ptolémaïque, en se confinant aux conceptions géocentriques[55]. Comme le note en effet l’historien des sciences A. I. Sabra :
« On sait que tous les astronomes arabes, de Thabit ibn Qurra au IXe siècle à Ibn al-Shatir au XIVe siècle, et tous les philosophes de la nature d’al-Kindi à Averroès et même après, ont accepté ce que Kuhn appelle l’« univers à deux sphères » ...—les Grecs se représentent le monde comme formé de deux sphères dont l'une, la sphère céleste, faite d'un élément particulier appelé « éther », entoure la seconde, où les quatre éléments (terre, eau, air, et feu) sont confinés[56] ».
Certains astronomes musulmans, toutefois, notamment Abū Rayhān al-Bīrūnī et Nasir ad-Din at-Tusi, se demandèrent si la Terre n’était pas elle-même en mouvement et recherchèrent comment rendre cette hypothèse compatible avec les calculs astronomiques et les principes cosmologiques[57]. Plusieurs autres astronomes musulmans, et particulièrement les disciples de l’École de Maragha, mirent au point des modèles planétaires, qui, tout en restant géocentriques, divergeaient de celui de Ptolémée : ils devaient plus tard être adaptés au modèle de Copernic dans le cadre de l’héliocentrisme.
Réfutation de l'astrologie
Article détaillé : astrologie.La première distinction sémantique entre astronomie et astrologie est attribuée à l'astronome persan al-Biruni au XIe siècle[58], bien qu’il ait lui-même réfuté l’astrologie dans un autre de ses livres. D'autres astronomes contemporains, dont al-Farabi, Alhazen, Avicenne et Averroès, critiquaient d'ailleurs cette discipline, pour des motifs tantôt scientifiques (les méthodes des astrologues étant plus conjecturales qu'expérimentales) tantôt religieux (conflits avec les savants musulmans orthodoxes[59]).
Ibn Qayyim al-Jawziyya (1292-1350), dans son Miftah Dar al-SaCadah, employait des arguments expérimentaux pour réfuter l’astrologie et la divination[60]. Il découvrit que les étoiles sont bien plus grosses que les planètes, et en tira l'argument suivant[61] :
« Et si vous autres, astrologues, répondez que c'est précisément à cause de leur éloignement et de leur petite taille que leur influence est négligeable, alors pourquoi attribuez-vous une si grande influence au plus petit de tous les astres, Mercure? Et pourquoi avez-vous attribué une influence à al-Ra's et al-Dhanab, qui sont deux points imaginaires [les nœuds ascendants et descendants]? »
Al-Jawziyya découvrit aussi que la Voie lactée est une « myriade de minuscules étoiles groupées ensembles sur la sphère des fixes » et en conclut qu’« il est certainement impossible de pouvoir connaître leur influence[61]. »
Astrophysique et mécanique céleste
En astrophysique et mécanique céleste, al-Biruni définit la gravitation de la Terre comme[62] : « L’attraction de toute chose vers le centre de la Terre. »
Al-Biruni découvrit aussi que la gravité existe aussi pour les corps célestes et les sphères célestes, et il critiqua l’opinion aristotélicienne qui leur refuse toute légèreté ou gravité, et qui font du mouvement circulaire une propriété intrinsèque des corps célestes[63].
En 1121, al-Khazini, dans son traité Le Livre de la Balance de Sagesse, affirme[64] : « Pour chaque grave de poids connu placé à une certaine distance du centre de l’univers, sa gravité dépend de son éloignement au centre de l’univers. C'est pourquoi les gravités des corps sont entre elles comme leurs distances relatives au centre de l’univers. »
Al-Khazini est ainsi le premier à avoir proposé une théorie du poids des corps qui dépende de leur distance au centre de la Terre. Ce phénomène ne devait pas recevoir de preuve avant celle de Newton pour la loi universelle de la gravitation au XVIIIe siècle[64].
Les débuts de la tradition hay'a
Entre 1025 et 1028, Ibn al-Haytham (latinisé en « Alhazen »), initia la tradition haya en astronomie arabe avec son livre intitulé Al-Shuku ala Batlamyus (Critique de Ptolémée). Tout en confirmant la réalité physique du géocentrisme, il fut le premier à remettre en cause le système planétaire de Ptolémée, qu'il critiqua pour des raisons expérimentales, pour leur incompatibilité avec les observations du ciel[65], et pour relier les véritables mouvements des astres à des points, lignes et cercles imaginaires : « Ptolémée fait l'hypothèse d’un ordre qui ne peut exister, et le fait que cet ordre reconstitue pour son imagination des mouvements qui sont ceux des planètes ne l’exonère pas de l'erreur qu’il a commise en faisant l’hypothèse de cet ordre ; car les mouvements réels des planètes ne peuvent résulter d’un ordre qui n'existe pas[66]. »
Alhazen élabora un mécanisme du système de Ptolémée dans son Traité de la figure du monde (Maqâlah fî hay'at al-‛âlam), ouvrage qui occupe une place centrale dans le corpus de la tradition hay’a[67]. Dans son Abrégé d'astronomie, il insiste sur le fait que les astres « sont justiciables des lois physiques[68]. » On peut aussi faire remonter les bases de l’astronomie télescopique à Alhazen, par l’influence de ses études sur l’optique sur le cours ultérieur de l’optique instrumentale[69].
En 1038, Alhazen décrivit le premier modèle non ptolémaïque dans son traité sur Le Modèle des Mouvements. Cette proposition était étrangère aux préoccupations cosmologiques, car il ne s'agissait là que d'une cinématique céleste purement géométrique ; mais elle suscita diverses innovations de géométrie infinitésimale[70]. Ce nouveau modèle était le premier à rejeter équants[71] et cercles déférents[72], à extraire l’astronomie de la philosophie naturelle, à délivrer la cinématique céleste de la cosmologie, et à abstraire les entités physiques en entités géométriques. Il faisait aussi intervenir une rotation de la Terre autour de l'axe des pôles[73] et les centres des orbites étaient des points géométriques sans signification matérielle particulière, comme le ferait des siècles plus tard Johannes Kepler[74]. Alhazen développe également une version primitive du « rasoir d'Occam », en tâchant de faire le minimum d'hypothèses sur les propriétés caractéristiques des mouvements astraux, dans la mesure où il essaye d’éliminer de son modèle planétaire les hypothèses cosmologiques qu'on ne peut observer de la Terre[75].
 Al-Biruni fut le premier à mener des expériences élaborées touchant les phénomènes célestes, il calcula l’accélération des planètes, découvrit que les mouvements apogée solaire et la précession sont distinctes, discuta la possibilité de l’héliocentrisme, et établit que la rotation propre de la Terre autour de l'axe des pôles n'était pas contradictoire avec les observations.
Al-Biruni fut le premier à mener des expériences élaborées touchant les phénomènes célestes, il calcula l’accélération des planètes, découvrit que les mouvements apogée solaire et la précession sont distinctes, discuta la possibilité de l’héliocentrisme, et établit que la rotation propre de la Terre autour de l'axe des pôles n'était pas contradictoire avec les observations.
Nouveaux modèles du cosmos
En 1030, al-Biruni commenta les théories indiennes d’Âryabhata, Brahmagupta et Varahamihira dans ses Ta'rikh al-Hind (traduits sous le titre d’Indica). Biruni y rapporte que Brahmagupta et d'autres considèrent que la Terre tourne autour de son axe polaire et il remarque que cela n’entraîne aucun problème au plan mathématique[76].
Al-Sijzi-Abu Said Al-Sijzi, un contemporain d’al-Biruni, émit l'hypothèse que la Terre tourne autour du Soleil, ce qu’al-Biruni de démentit pas[77]. En fait, Al-Biruni était surtout convaincu de la rotation de la Terre autour de l'axe des pôles, et, si au début il resta silencieux au sujet des thèses héliocentriques et géocentrique[78], il finit par considérer l’héliocentrisme comme un problème philosophique[3]. Il remarqua que le fait que la Terre tourne sur elle-même et qu'elle accomplit en même temps une révolution autour du Soleil, n’était pas contradictoire avec ses propres observations du ciel[62],[79] : « La rotation de la Terre ne remettrait aucunement en cause les calculs astronomiques, car toutes les données astronomiques peuvent être expliquées indifféremment par l'une ou l'autre théorie. C'est donc un problème difficile à trancher. »
En 1031, al-Biruni paracheva son encyclopédie astronomique intitulée Kitab al-Qanun al-Mas'udi (traduite en latin sous le titre de Canon Masudicus)[80], dans laquelle il consigna ses découvertes astronomiques et publia ses tables astronomiques. Il y proposait un modèle géocentrique, avec un tableau des distances de toutes les sphères célestes depuis la Terre, calculées selon les principes de l’Almageste de Ptolémée[81]. Ce livre fournit une technique mathématique de calcul de l’accélération des planètes, et établit pour la première fois que l’apogée solaire et la précession sont distinctes. Al-Biruni découvrit en outre que la distance entre la Terre et le Soleil est plus grande en réalité que l’estimation que donnait Ptolémée, dans la mesure où Ptolémée négligeait les éclipses de Soleil annuelles[62],[82].
En 1070, Abu Ubayd al-Juzjani, un disciple d’Avicenne, proposa un modèle non-ptolémaïque dans son traité Tarik al-Aflak. Dans ce livre, il formule le problème dit de l’équant du modèle de Ptolémée, et y propose une solution. Il affirme qu’Avicenne avait lui-même résolu le problème de l’équant[83].
La controverse andalouse
 Averroès rejetait la théorie des cercles déférents proposée en son temps par Ptolémée. Pus généralement, il n'acceptait pas le modèle ptolémaïque et était partisan d'un modèle d’univers concentrique.
Averroès rejetait la théorie des cercles déférents proposée en son temps par Ptolémée. Pus généralement, il n'acceptait pas le modèle ptolémaïque et était partisan d'un modèle d’univers concentrique.
Au tournant des XIe et XIIe siècles, des astronomes d’al-Andalus relevèrent le défi d’Alhazen, à savoir développer un modèle de sphères qui éviterait les erreurs du modèle de Ptolémée qu'il avait relevées[84]. Comme la critique d’Alhazen, l'ouvrage anonyme andalous intitulé al-Istidrak ala Batlamyus (Récapitulation de Ptolémée) comportait une liste des objections à Ptolémée. C’est le point de départ de la controverse andalouse sur l'astronomie de Ptolémée[85]
À la fin du XIe siècle, Arzachel découvrit que les orbites des planètes sont elliptiques et non circulaires[86], bien qu'il respectât encore le système de Ptolémée.
Au XIIe siècle, Averroès rejetait la théorie des cercles déférents proposée en son temps par Ptolémée, tout comme il repoussait le modèle ptolémaïque : il était partisan du modèle d’univers concentrique d'Aristote[87]. Il écrivit sur le système planétaire de Ptolémée la critique suivante[1] :
« Il est contraire à la Nature de supposer l’existence d'une sphère excentrique ou d'un épicycle. [...] L’astronomie contemporaine ne nous présente aucune vérité, elle n'est conforme qu’à des calculs, non à la réalité. »
Un contemporain d’Averroès, Maïmonide, écrivit à propos du modèle planétaire d’Avempace :
« J’ai entendu dire qu’Abu Bakr [Avenpace] avait découvert un système où il n'y a plus d’épicycles, mais il n’en a pas exclu les sphères excentriques. Ses disciples ne me l’ont pas dit ; et même s’il est vrai qu’il ait découvert un tel système, il n’y a pas gagné grand chose, car l’excentricité est tout aussi contraire aux principes posés par Aristote.... Je t’ai expliqué que ces difficultés ne concernent pas l’astronome, car il ne prétend pas enseigner les propriétés véritables des sphères, mais de simplement suggérer une théorie, exacte ou non, dans laquelle le mouvement des étoiles et des planètes est uniforme et circulaire, et en accord avec l’observation[88]. »
Par ailleurs, Ibn Bajjah était d’avis que la Voie lactée est faite d’un grand nombre d’étoiles mais que la réfraction de l’atmosphère terrestre lui donne l’aspect d'un voile continu[49]. Plus tard dans le XIIe siècle, ses successeurs Ibn Tufayl et Alpetragius proposèrent pour la première fois des modèles planétaires dépourvus d’équants, épicycles ou excentriques. Alpetragius découvrit également le premier que les planètes ont leur luminosité propre[89]. Ces systèmes planétaires, cependant, furent rejetés car les prédictions des positions des planètes étaient moins précises qu’avec le modèle de Ptolémée[90], essentiellement parce qu’ils s’en tenaient au dogme d’Aristote de mouvement circulaire parfait.
L'École de Maragha
Article détaillé : Maragha#L'observatoire.L’École de Maragha est à l’origine d’une critique radicale de l’astronomie ptolémaïque. Cette tradition astronomique commence avec l’institution de l'observatoire de Maragha et se poursuit avec l'œuvre des astronomes de Damas et de Samarkande. Comme leurs prédécesseurs d’Andalousie, les astronomes de Maragha s'essayèrent à la résolution du problème de l’équant et proposèrent leurs alternatives au modèle ptolémaïque, et le supplantèrent en ceci qu'ils parvinrent à supprimer les constructions auxiliaires de Ptolémée (équant et excentriques), avec une précision supérieure dans le calcul numérique de la position des planètes, c’est-à-dire avec une meilleure concordance avec les données d’observation[91]. Les astronomes les plus éminents de l’École de Maragha sont Mo'ayyeduddin Urdi († 1266), al-Tūsī (1201-1274), 'Umar al-Katibi al-Qazwini († 1277), Qutb al-Din al-Shirazi (1236-1311), Sadr al-Sharia al-Bukhari (vers 1347), Ibn al-Shatir (1304-1375), Ali Qushji (vers 1474), al-Birjandi († 1525) et Shams al-Din al-Khafri († 1550)[92].
 al-Tūsī parvint à résoudre plusieurs difficultés posées par le modèle ptolémaïque en introduisant un mouvement d’hypocycloïde, qui devait par la suite retrouver sa place dans le modèle de Copernic.
al-Tūsī parvint à résoudre plusieurs difficultés posées par le modèle ptolémaïque en introduisant un mouvement d’hypocycloïde, qui devait par la suite retrouver sa place dans le modèle de Copernic.
On a pu qualifier leurs réalisations aux XIIIe siècle et XIVe siècle comme la « Révolution Maragha », la « Révolution de l’École de Maragha », ou encore une « Révolution scientifique antérieure à la Renaissance ». Un acquis important de cette révolution est la prise de conscience que l’astronomie ne doit plus se borner à décrire le mouvement des corps physiques en langage mathématique, ou n’être qu’une hypothèse mathématique, ce qui ne ferait que sauver les apparences (pour reprendre l'expression de P. Duhem). Les astronomes de Maragha se convainquirent aussi que le précepte aristotélicien, selon lequel les mouvements dans l'univers ne peuvent être que circulaires ou rectilignes est faux, puisque l’hypocycloïde d'Al-Tusi montre qu’on peut engendrer un mouvement rectiligne uniquement à partir de mouvements circulaires[93].
À la différence des astronomes grecs qui ne se préoccupaient que de la cohérence entre les axiomes mathématiques et les principes physiques du mouvement des planètes, les astronomes arabes s’efforçaient d'adapter les mathématiques au monde qui les entourait[94] permettant un passage de la Physique d’Aristote à la physique expérimentale et à la physique mathématique à la suite des travaux d’Ibn al-Shatir. La Révolution Maragha est donc caractérisée par une prise de distance avec les bases philosophiques de la cosmologie aristotélicienne et de l’astronomie géocentrique, par un plus grand poids accordé à l’observation et à la mathématisation de l’astronomie et des sciences naturelles en général, comme on le voit dans les œuvres d’Ibn al-Shatir, d’al-Qushji, d’al-Birjandi et d’al-Khafri[95],[96],[97].
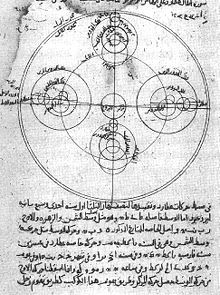 Modèle d’Ibn al-Shatir pour l’apparition de Mercure, montrant la multiplication des épicycles fondés sur l’hypocycloïde d'Al-Tusi, éliminant par ce moyen les cercles déférents et l’équant introduits précédemment par Ptolémée.
Modèle d’Ibn al-Shatir pour l’apparition de Mercure, montrant la multiplication des épicycles fondés sur l’hypocycloïde d'Al-Tusi, éliminant par ce moyen les cercles déférents et l’équant introduits précédemment par Ptolémée.
Parmi les autres progrès dont on est redevable à l’École de Maragha, citons les premières observations prouvant la rotation de la Terre sur elle-même par al-Tusi et al-Qushji[98], l'autonomie donnée par Ibn al-Shatir et al-Qushji à l’astronomie par rapport à la philosophie naturelle[99], la réfutation par Ibn al-Shatir du modèle de Ptolémée sur des raisons expérimentales plutôt que philosophiques[91], et la conception d'un modèle mathématiquement identique au modèle de Copernic par Ibn al-Shatir[100].
Mo'ayyeduddin Urdi († 1266) fut le premier des astronomes de Maragha à imaginer un modèle planétaire non ptoléméen, et proposa à cet effet un nouveau théorème, le « lemme Urdi[101]. » Nasir ad-Din at-Tusi (1201-1274), à l'aide de l’hypocycloïde qui porte son nom (et dont le principe est celui de l'engrenage de La Hire) parvint à résoudre une grande partie des difficultés propres au système de Ptolémée en se passant du problématique équant imaginé par l'astronome grec[102], et construisit un modèle à orbites elliptiques[80]. Un de ses disciples, Qutb al-Din al-Shirazi (1236-1311), dans un traité intitulé Le summum de la connaissance des cieux, examina la possibilité de l’héliocentrisme. 'Umar al-Katibi al-Qazwini († 1277), qui était également actif à l'observatoire de Maragha, rapporta dans son Hikmat al-'Ain un argument en faveur du modèle héliocentrique, bien qu'il ait abandonné cette doctrine par la suite[77].
Ibn al-Shatir (1304–1375) de Damas publia dans son livre Ultime tentative pour corriger la Théorique des planètes le « lemme Urdi », et parvint à supprimer l'équant en introduisant un épicycle supplémentaire (l’hypocycloïde de Tusi), corrigeant le système de Ptolémée d'une façon mathématiquement analogue à celle de Nicolas Copernic au XVIe siècle. À la différence des astronomes qui l'avaient précédé, Ibn al-Shatir ne cherchait pas à préserver les principes théoriques de la philosophie naturelle ou de la cosmologie aristotélicienne, mais plutôt à établir un modèle plus cohérent avec les observations. C’est d'’ailleurs ce souci empirique qui le poussa à éliminer les épicycles du système solaire et tous les excentriques, épicycles et l'équant du système lunaire de Ptolémée. Ainsi, son modèle surpassa en précision tous les autres[91], et fut le seul à permettre de faire des expériences[103]. Cette démarche, qui marque un tournant dans l'histoire de l'astronomie, a pu être qualifiée de « Révolution Scientifique d’avant la Renaissance[91]. » Avec quelques modifications (inverser la direction du rayon-vecteur Terre-Soleil[3]), Copernic en fit un modèle héliocentrique[102]. Dans la version imprimée de son chef d’œuvre, De revolutionibus orbium coelestium, Copernic cite aussi les théories d’al-Battani, d’Arzachel et d’Averroès parmi ses sources[80], mais les ouvrages d’Alhazen et d’al-Biruni étaient aussi déjà connus en Europe à cette époque.
Un thème d’intenses débats à l’École de Maragha, et plus tard dans les observatoires de Samarkande et d’Istanbul, était l'éventualité de la rotation de la Terre. Parmi les partisans de cette théorie, on comptait Nasir ad-Din at-Tusi, Nizam al-Din al-Nisaburi (vers 1311), al-Sayyid al-Sharif al-Jurjani (1339-1413), Ali al-Qushji (d. 1474), et Abd al-Ali al-Birjandi (d. 1525). Al-Tusi le premier présenta des preuves fondées sur des observations de la rotation de la Terre, en se servant des positions des comètes par rapport à la Terre, une démonstration qu’al-Qushji renforça avec de nouvelles observations tout en dénonçant la philosophie naturelle d’Aristote. Leur arguments sont identiques à ceux qu'utilisera Nicolas Copernic en 1543 pour expliquer la rotation de la Terre[98].
L’astronomie arabe et la Chine
Article détaillé : Astronomie chinoise.On fit venir en Chine sous la Dynastie Yuan des astronomes musulmans pour y perfectionner le calendrier et enrichir l'astronomie. Au cours du règne de Kubilai Khan, des Iraniens vinrent construire un observatoire et un institut d'études astronomiques à Pékin[104]. Un astronome persan, Djamal ad-Din, offrit en 1267 à Kubilai Khan un coffret de sept instruments astronomiques, comprenant un globe et une sphère armillaire[105]. On sait par ailleurs que plusieurs astronomes chinois travaillaient à l’observatoire de Maragha, en Perse.
La stagnation (1450-1900)
On considère cette période de plus de quatre siècles comme marquée par une stagnation : la pratique traditionnelle de l’astronomie dans le monde musulman reste soutenue, mais par comparaison aux siècles précédents et surtout le monde extérieur, l’innovation se tarit assez vite[21]. Si pour la plupart des chercheurs il n'y a plus de progrès marquant durant cette période, quelques historiens ont récemment fait valoir que des innovations interviennent encore au XVIe siècle et même plus tard[99],[106]. Quoi qu’il en soit, après le XVIe siècle, il semble bien que l’intérêt pour l’astronomie théorique soit éteint, tandis qu'au contraire la pratique de l’astronomie d'observation selon la tradition arabe reste soutenue dans les trois empires musulmans de la poudre à canon : l’Empire ottoman, les Séfévides de Perse, et l’Empire moghol en Inde.
Le mouvement de la Terre
 Ali al-Qushji (ici présentant ses œuvres au sultan Mehmed Ier) fournit des preuves expérimentales du mouvement de la Terre et séparait entièrement l’astronomie de la philosophie naturelle.
Ali al-Qushji (ici présentant ses œuvres au sultan Mehmed Ier) fournit des preuves expérimentales du mouvement de la Terre et séparait entièrement l’astronomie de la philosophie naturelle.
L’œuvre d’Ali Qushji (†1474), qui vécut d'abord à Samarkande puis à Istamboul, est considérée comme un exemple de renouveau tardif de l’astronomie arabe et l'on estime qu'il a pu exercer une influence sur Nicolas Copernic du fait de la similitude d’arguments des deux auteurs sur la possibilité de la rotation de la Terre. Avant Ali Qushji, le seul astronome qui avait présenté un argument empirique en faveur de la rotation de la Terre était Nasir ad-Din at-Tusi (†1274) : il s'appuyait sur le phénomène des comètes pour réfuter la thèse de Ptolémée selon laquelle on peut prouver par la seule observation que la Terre est immobile. Al-Tusi, cela dit, convenait que la Terre était immobile en se référant aux arguments de philosophie naturelle du Traité du Ciel d’Aristote. Au XVe siècle, les oppositions religieuses mirent un frein à l’influence de la physique et de la philosophie naturelle. Ainsi Al-Qushji, dans son pamphlet Sur le caractère prétendument subalterne de l’Astronomie par rapport à la Philosophie, dénonçait la physique d’Aristote et dut séparer entièrement la philosophie de l’astronomie, pour permettre à cette dernière de s’épanouir en tant que discipline empirique et mathématique. Il put ainsi examiner les alternatives au dogme aristotélicien de la Terre immobile. Il développa la thèse d’al-Tusi et conclut, se fondant davantage sur l’expérience que sur la philosophie spéculative, que la théorie d'une Terre en mouvement est tout aussi plausible que celle de la Terre immobile, et qu’il est impossible de discriminer empiriquement si l'une de ces deux thèses est vraie[98],[99],[107].
Au XVIe siècle, le débat sur le mouvement de la Terre fut relancé par al-Birjandi (†1528), lequel, se demandant quels phénomènes devraient accompagner la rotation de la Terre, en vient à formuler une hypothèse similaire à l’inertie de rotation de Galilée[108], qu'il évoque (en réponse à une objection de Qutb al-Din al-Shirazi) à propos de l'observation suivante :
« Le rocher, grand ou petit, tombe vers la Terre selon une ligne perpendiculaire au plan (sath) de l’horizon ; l'expérience (tajriba) en témoigne. Et cette perpendiculaire s'écarte du point de tangence de la sphère de la Terre et du plan de l’horizon apparent (hissi). Ce point suit le mouvement de la Terre et c'est pourquoi il n'y a pas de différence quant au point de chute des deux rochers[109]. »
Astronomie théorique
On pensait jusqu'à la fin du XXe siècle que les progrès des astronomes arabes dans la théorique des planètes avaient pris fin avec l'œuvre d’Ibn al-Shatir au XIVe siècle, mais de nouvelles recherches ont mis en lumière les découvertes remarquables accomplies jusqu'au XVIe siècle, notamment à la suite des travaux de George Saliba sur Shams al-Din al-Khafri (†1550), un glossateur séfévide des écrits des astronomes de Maragha. Saliba écrit à propos d’al-Khafri :
« Par sa perception claire du rôle des mathématiques dans la description des phénomènes naturels, cet astronome réussit à porter la tradition hay’a à des sommets inégalés ailleurs, au plan mathématique comme au plan astronomique. La recherche de modèles mathématiques pouvant supplanter celui de Ptolémée, et l'examen des œuvres de ses prédécesseurs tous en quête d'un modèle mathématique unifié à même de rendre compte de tous les phénomènes physiques, lui firent conclure que toute modélisation mathématique n’a pas par elle-même de sens physique, et qu’elle n’est qu'un langage parmi d'autre pour décrire la réalité physique. Il se persuada également que les phénomènes décrits par les modèles ptoléméens n’admettent pas de solution mathématique unique soumise aux mêmes contraintes ; qu’au contraire il existe plusieurs modèles mathématiques capables de rendre compte des observations de Ptolémée ; qu’ils aboutissent aux mêmes prévisions sur les points critiques que Ptolémée avait retenus pour construire ses propres modèles (et qu’ainsi ils ne rendent pas mieux compte des observations que Ptolémée) tout en respectant les conditions imposées par la cosmologie aristotélicienne, admise par les auteurs de la tradition hay’a[106]. »
Ali al-Qushji améliora aussi le modèle planétaire d’al-Tusi et proposa une alternative au modèle de l'orbite de Mercure[110].
L'astronomie d'observation dans l'empire ottoman
Autre astronome musulman fameux du XVIe siècle, l’Ottoman Taqi al-Din fit construire en 1577 l’Observatoire d’Istamboul, où il put observer le ciel jusqu’en 1580. Il dressa des tables Zij (intitulées La perle intacte) et des catalogues astronomiques plus précis que ceux, contemporains, de Tycho Brahe et de Nicolas Copernic. Al-Din est aussi le premier astronome à utiliser la notation à virgule plutôt que les traditionnelles fractions sexagésimales dans les compte-rendus de ses observations[111]. Il inventa aussi entre 1556 et 1580 de nombreux instruments astronomiques, parmi lesquels de très précises horloges astronomiques.
Déjà en 1574, al-Din s'était appuyé sur ses connaissances d’astrophysique pour expliquer la doctrine de l’intromission de la vision : il avança que, puisque les étoiles sont distantes de millions of kilomètres de la Terre et que la vitesse de la lumière est finie, il faudrait un temps très long pour que la lumière « aille vers l'étoile et revienne à nos yeux. mais tel n'est pas le cas, car nous voyons l'étoile dès que nous ouvrons les yeux. Donc la lumière doit venir de l'étoile, et non de l’œil[112]. »
À la destruction de l’observatoire d’Istanbul en 1580, l’activité astronomique stagna dans l’Empire ottoman, jusqu’à l’introduction de la Révolution copernicienne en 1660, avec la traduction par l'érudit ottoman Ibrahim Efendi al-Zigetvari Tezkireci en arabe de la « Nouvelle théorie des planètes » de Noël Duret (publiée en 1635)[113].
L'astronomie arabe en Inde
Du XVIe au XVIIe siècle, l’Empire moghol vit naître une synthèse entre l’astronomie arabe et l’astronomie indienne, avec l'association des techniques et des instruments d’observation arabe et des techniques de calcul hindoues. S’il semble qu'il n'y ait guère eu d'intérêt pour l’astronomie théorique, astronomes musulmans et hindous en Inde firent encore de nouveaux progrès dans l’astronomie d'observation et publièrent une centaine de traités Zij. Humâyûn se fit construire un observatoire particulier près de Delhi, et Jahângîr et Shâh Jahân l'envisagèrent également, sans toutefois pouvoir y parvenir. Après le déclin de l’Empire moghol, pourtant, c'est un roi hindou, Jai Singh II d’Ambre, qui entreprit de faire renaître la tradition astronomique arabe dans son royaume. Au début du XVIIIe siècle, il fit édifier plusieurs grands observatoires appelés Yantra Mandirs afin de pouvoir rivaliser avec le fameux observatoire de Samarkande, et mettre à jour les tables sultaniennes d’Ulugh Beg par des observations plus précises. Les instruments et les techniques d’observation mis en œuvre à l’observatoire étaient pour la plupart issus de la tradition islamique, et les techniques de calcul, de la tradition hindoue[114],[115]. En particulier, l’un des plus remarquables instruments astronomiques inventés par les Musulmans dans l’Inde des Moghols est le « globe céleste sans soudure » (cf. infra Globes).
Jai Singh invita par ailleurs à son observatoire des astronomes européens jésuites, qui lui avaient rapporté les tables astronomiques compilées par Philippe de La Hire en 1702. À la lecture du livre de La Hire, Jai Singh conclut que les techniques et les instruments des Européens étaient moins bons que ceux de son pays. On ignore si les astronomes musulmans de l’Inde ont appris la Révolution copernicienne des jésuites, mais comme ils ne s'intéressaient plus à l'astronomie théorique, les spéculations venues d’Europe n'étaient plus susceptibles de retenir leur attention[116].
L’astronomie dans le monde arabe (depuis 1900)
Au XXe et au XXIe siècles, les astronomes musulmans ont réalisé de nouvelles avancées dans l'observation de la Lune, tandis que des astronautes et fuséologues musulmans ont participé à la recherche en astronautique et aux programmes internationaux de recherche spatiale.
Implication des pays arabes dans la recherche spatiale
Fichier:Kerimov21.jpgKerim Kerimov, l'un des pionniers du Programme spatial de la Russie.L'Azéri Kerim Kerimov (alors citoyen de l’Union Soviétique) est un personnage-clef des débuts de l’exploration spatiale. Il est l'un des pionniers du Programme spatial soviétique, l'un des architectes à l’œuvre derrière les premiers vols spatiaux habités (Vostok 1). Il a été responsable du lancement des premières stations spatiales (programmes Salyout et Mir) et des programmes antérieurs (Cosmos 186 et Cosmos 188)[117],[118].
L’Égyptien Farouk El-Baz travaillait, lui, pour le programme concurrent de la NASA et prit part aux premiers atterrissages sur la Lune avec le programme Apollo, en tant que secrétaire du Landing Site Selection Committee, Principal Investigator of Visual Observations and Photography, président du Astronaut Training Group, participa à la planification des explorations scientifiques de la Lune, y compris le choix des sites d'atterrissage pour les missions Apollo et l'entraînement des astronautes aux observations et à la photographie lunaire[119].
À la fin du XXe et au début du XXIe siècle, on compte aussi déjà un certain nombre d’astronautes musulmans, dont le premier est le sultan Salman Al-Saud en tant qu’expert étranger, à bord de la Navette spatiale Discovery STS-51-G, suivi de Muhammed Faris à bord de Soyouz TM-2 et Soyouz TM-3 à bord de la station spatiale Mir ; Abdul Ahad Mohmand à bord de Soyouz TM-5 pour Mir ; Talgat Musabayev (l’un des 50 astronautes restés le plus longtemps dans l’espace) en tant qu’ingénieur de vol à bord de Soyouz TM-19 pour Mir, commandant de bord de Soyouz TM-27 pour Mir, et commandant de bord de Soyouz TM-32 et Soyouz TM-31 pour Station spatiale internationale (SSI) ; enfin Anousheh Ansari, la première femme à travailler à la SSI et le quatrième touriste spatiale.
En 2007, le cheikh malais Muszaphar Shukor rejoignit pendant le Ramadan la SSI avec son équipage Expédition 16 à bord de Soyouz TMA-11 dans le cadre du programme Angkasawan. Pour l’occasion, le National Fatwa Council édicta des Règles pour l'accomplissement des rites islamiques (Ibadah) dans la Station spatiale internationale, sur des sujets comme la prière en impesanteur, la recherche de la direction de La Mecque depuis l’ISS, la détermination des heures de prière, et la pratique du jeûne. Shukor célébra aussi l’Aïd el-Fitr à bord de l’ISS. Astronaute et orthopédiste, il fut le premier à effectuer des recherches biomédicales dans l'espace, en particulier en ce qui concerne la multiplication des cellules cancéreuses du foie et la leucémie, la cristallisation de diverses protéines et la multiplication des microbes[120].
Parmi les plus grands chercheurs musulmans qui participent à la recherche et à l'exploration spatiale, on compte Essam Heggy, qui travaille pour la NASA sur le Programme d’Exploration de Mars, au Lunar and Planetary Institute de Houston ; et Ahmed Salem, Alaa Ibrahim, Mohamed Sultan, et Ahmed Noor[121].
Progrès dans l'observation de la Lune
Selon l’islam, les musulmans doivent accomplir des rites religieux certains jours fixés par le calendrier musulman. C'est pourquoi l’observation de la Lune joue un si grand rôle[122]. Récemment, avec les moyens fournis par télécommunications et les nouvelles technologies pour déterminer l'heure de la nouvelle Lune, une nouvelle tendance est apparue chez les musulmans[123],[124],[125] et de nouvelles questions religieuses se sont posées[126].
En 2005, l’ayatollah Ali Khamenei, Faqih et Rahbar d’Iran, a promulgué une fatwa contre le recours aux technologies modernes pour les Salah. L’Islamic Society of North America de Plainfield (Indiana), a intenté un procès l'année suivante. Les musulmans rivalisent de prouesses technologiques lors du rituel annuel de détection de la Lune[122],[127].
L’ayatollah Khamenei a créé un Comité d’Observation de la Lune, composé de clercs qui dépouillent les observations recueillies dans les différents centres d'observation. Les chercheurs notent l’angle de la Lune, sa position, son illumination, et comparent les observations du terrain avec les cartes calculées qui indiquent en quel point la Lune doit se trouver. En Iran, des groupes d’astronomes accompagnés chacun d'un clerc sont dépêchés à travers le pays, certains utilisant des jumelles infrarouges prêtées par l’armée iranienne et des lunettes astronomiques à haute résolution prêtés par les universités. L’Iran missionne également chaque année un avion pour l’observation. Cet avion est équipé d’appareils photographiques et d’instruments de haute précision, ainsi que d’un ordinateur portable. Des cartographes iraniens de la National Geography Organization in Téhéran ont pu dessiner une carte tridimensionnelle de la région en positionnant les 70 points d'où l'on peut le mieux voir la nouvelle Lune[122]. Il y a d’autres tentatives similaires dans d'autres pays musulman.
Les astronomes se lancent aussi dans une compétition sur la détection de la nouvelle Lune à l’œil nu. Selon le calendrier islamique en vigueur en Iran, le dernier « World Record for Lunar Crescent Sighting » a été battu le 7 septembre 2002 (le 29 Jamadi-al Thani 1423 de l’Hégire) par Mohsen Ghazi Mirsaeed sur les hauteurs nord-ouest de Zarand (2 110 m) dans le village de Rashk Bala (). Le record pour l'âge de la nouvelle Lune à la première perception à l’œil nu est 11 heures 42 minutes[128].
Observatoires
L’observatoire astronomique moderne en tant qu’institut de recherches[129] (à la différence des postes d’observation privés tels qu’ils existaient dans l’Antiquité[130]) est une conception des astronomes musulmans, qui rédigèrent les traités Zij grâce à ces observatoires. L’observatoire islamique fut la première institution astronomique spécialisée avec un personnel scientifique[129], un directeur, un programme d’études[130], et des locaux où s'accomplissaient la recherche astronomique et les observations. Les observatoires islamiques furent également les premiers centres de recherche à avoir recours à de grands instruments pour améliorer la précision des observations[129].
Les observatoires islamiques médiévaux étaient aussi les premières institutions à promouvoir le travail d’équipe (au contraire de la recherche individuelle) et où « les investigations théoriques marchaient main dans la main avec l’observation. » En ce sens, ils étaient semblables aux modernes instituts de recherche scientifique[131].
Premiers observatoires
Les sources signalent que les premières observations astronomiques dans la civilisation islamique ont été accomplies grâce au mécénat d’al-Ma'moun, et les premiers observatoires islamiques furent aussi construits sous son règne dans l’Irak du IXe siècle. Dans plusieurs observatoires privés, de Damas à Bagdad, on mesurait déjà les degrés méridien, on notait les paramètres solaires, et on menait des observations précises du Soleil, de la Lune, et des planètes.
Au Xe siècle, la dynastie des Bouyides encouragea des grands projets, comme la construction d'un instrument de grande taille utilisé en 950 pour l’observation du ciel : cela nous est connu par les tables zij d’astronomes comme Ibn al-Alam. Le célèbre astronome Abd Al-Rahman Al Sufi, un protégé du prince 'Adud al-Dawla, rectifia systématiquement le catalogue d’étoiles de Ptolémée. Abu-Mahmud al-Khujandi, lui aussi, construisit un observatoire à Ray (Teheran) où l'on sait qu'il a fait dresser un monumental sextant mural en 994[132]. Charaf ad-Dawla Chirzil construisit un observatoire semblable à Bagdad. On connaît enfin par Ibn Yunus à Tolède, et Al-Zarqali à Cordoue les instruments perfectionnés qu'on utilisait déjà.
C'est Malik Shah Ier qui institua le premier grand observatoire, sans doute à Ispahan. C'est là qu’Omar Khayyam et ses collaborateurs construisirent leurs tables et promulguèrent le Calendrier solaire persan, également appelé calendrier jalali, à l’époque le plus précis calendrier solaire. Une version moderne de ce calendrier est toujours d'usage officiel dans l’Iran actuel.
 L’observatoire de Maragha aujourd’hui.
L’observatoire de Maragha aujourd’hui.
Observatoires de la fin du Moyen Âge
Les observatoires les plus réputés, cependant, ne furent établis qu'à partir du début du XIIIe siècle. al-Tusi fit édifier l’observatoire de Maragha grâce aux donations de Houlagou Khan au XIIIe siècle. les bâtiments comportaient une résidence personnelle pour Houlagou Khan, ainsi qu'une bibliothèque et une mosquée. Certains des meilleurs astronomes de l'époque s'y sont rendus, et leur collaboration a débouché pendant 50 ans sur d'importantes modifications successives au modèle de Ptolémée. Les observations d’al-Tusi et de son équipe ont été rassemblées par écrit dans les tables intitulées Zij-i Ilkhani.
 Hommage à Ulugh Beg, fondateur d'un grand observatoire à Samarkande, sur ce timbre des postes soviétiques.
Hommage à Ulugh Beg, fondateur d'un grand observatoire à Samarkande, sur ce timbre des postes soviétiques.
En 1420, le prince Ulugh Beg, lui-même astronome et mathématicien, fit construire un grand observatoire à Samarkande, dont les vestiges ont été retrouvés par une équipe russe en 1908. En 1577, Taqi al-Din bin Ma'ruf fit édifier le grand observatoire al-Din d’Istamboul, d'une taille comparable à ceux de Maragha et de Samarkande.
Dans l’Empire Moghol, Humâyûn se fit construire un observatoire particulier près de Delhi, et Jahângîr et Shâh Jahân l'envisagèrent également, sans toutefois pouvoir y parvenir. Après le déclin de l’Empire moghol, pourtant, c'est un roi hindou, Jai Singh II d’Ambre, qui entreprit de faire renaître la tradition astronomique arabe dans son royaume. Au début du XVIIIe siècle, il fit édifier plusieurs grands observatoires appelés Yantra Mandirs afin de pouvoir rivaliser avec le fameux observatoire de Samarkande, et mettre à jour les tables sultaniennes d’Ulugh Beg par des observations plus précises. Les instruments et les techniques d’observation mis en œuvre à l’observatoire étaient pour la plupart issus de la tradition islamique, et les techniques de calcul, de la tradition hindoue[114],[115].
Observatoires modernes
Aujourd'hui, on trouve plusieurs observatoires modernes en Jordanie[133], Palestine[134], Liban[135], Émirats arabes unis[136], Tunisie[137], etc. L’Iran dispose de matériel moderne à l’Université de Shiraz et l’Université de Tabriz. En décembre 2005, Physics Today a révélé les projets iraniens de s'équiper d'un télescope de 2 m d'ouverture[138].
Instruments
Nos connaissances sur les instruments utilisés ou fabriqués par les astronomes musulmans du Moyen Âge nous viennent essentiellement de deux sources : d’une part les instruments conservés dans les collections privées et des musées, d’autre part les copies de traités et les manuscrits du Moyen Âge parvenus jusqu'à nous.
Les musulmans tout en perfectionnant les instruments des Grecs et Chaldéens en y adjoignant de nouvelles échelles, inventèrent un arsenal de nouveaux outils d'observation : leur contribution à l’astronomie instrumentale est donc considérable. Beaucoup de ces instruments ont été imaginés ou construits pour les besoins du culte, comme la détermination de la qibla (direction de La Mecque) ou de l’heure des Salah.
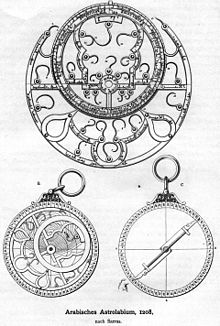
Astrolabes
On fabriqua des astrolabes en laiton partout dans le monde musulman, et on les utilisait surtout pout trouver la qibla. Le plus ancien spécimen date des années 927-928. On attribue la fabrication du premier astrolabe du monde musulman à Muhammad al-Fazari[139]. Bien que la civilisation hellénistique ait vu naître des astrolabes primitifs qui servaient à cartographier le ciel, al-Fazari l'a considérablement perfectionné. Les Arabes en systématisèrent l'usage et le perfectionnèrent pour déterminer notamment la date du Ramadan, les heures des prières (Salah), la direction de La Mecque (Qibla)[140].
Au Xe siècle, al-Soufi décrivait 1 000 utilisations possibles de l’astrolabe, dans des champs aussi divers que l’astronomie, l’astrologie, les horoscopes, la navigation maritime, la topographie, la mesure du temps, la Qibla, les Salah, etc[140].
- Grand astrolabe
Ibn Yunus releva soigneusement plus de 10 000 positions du Soleil pendant des années en se servant d’un astrolabe d’un diamètre de près de 1,40 m[37].
- astrolabe à engrenages
Les premiers astrolabes mécaniques à engrenages sont apparus dans le monde musulman, et ont été perfectionnés par Ibn Samh (vers 1020). Un de ces appareils, comportant huit roues dentées fut aussi fabriqué sur les indications d’Abū Rayhān al-Bīrūnī en 996. Ces instruments peuvent être considérés comme les ancêtres des horloges astronomiques mises au point ultérieurement par les ingénieurs arabes[141].
- Astrolabe de navigation
Le premier astrolabe de navigation est apparu dans le monde musulman au Moyen Âge, utilisait une projection polaire[142]/
- Astrolabe à projection orthographique
Abu Rayhan al-Biruni imagina et composa le plus ancien traité connu sur l’astrolabe orthographique autour de l'an mil[62].
- Scaphées et Zouraqi
Les premiers astrolabes étaient utilisés pour déterminer l'heure du lever et du coucher du Soleil et des étoiles fixes. Au XIe siècle, Arzachel d’al-Andalus construisit le premier astrolabe universel : à la différence de ses prédécesseurs, cet appareil ne dépendait plus de la latitude du lieu d’observation : on pouvait l'utiliser n'importe où sur Terre. L’astrolabe universel se répandit en Europe sous le nom grec de « scaphée ». Autre astrolabe, le zouraqi (cf. supra) imaginé par al-Sijzi est le seul conçu pour intégrer un modèle planétaire héliocentrique où c'est la Terre, et non les cieux, qui sont mobiles[40].
- Astrolabe linéaire
Dans un livre célèbre, al-Tūsī décrit un astrolabe linéaire de son crû, parfois appelé « bâton d’al-Tusi »[143]
- Horloges-astrolabes
Ibn al-Shatir a inventé cet appareil dans la Syrie du XIVe siècle[144].
Calcul analogique
On inventa plusieurs calculateurs analogiques pour calculer la latitude du Soleil, de la Lune et des planètes, l’écliptique du Soleil, la date des conjonctions planétaires et aussi pour effectuer des interpolations linéaires.
- Équatoire
L’Équatoire était un calculateur analogique inventé par Arzachel dans l’al-Andalus, probablement vers 1015. Cet appareil mécanique sert à trouver les longitudes et positions de la Lune, du Soleil, et des planètes sans calcul. Il s'appuie sur un modèle géometrique rendant compte de la position et de l’anomalie moyenne des astres[145].
- Planisphère et carte des étoiles
Au début du XIe siècle, Abū Rayhān al-Bīrūnī composa le premier traité sur le planisphère, la plus ancienne carte du ciel, et sur un calculateur analogique primitif[146],[62].
- Calendrier perpétuel à engrenages
Abū Rayhān al-Bīrūnī inventa aussi le premier calendrier luni-solaire à calculateur mécanique utilisant un train d’engrenages et huit roues dentées[147]. C'est là un exemple primitif de machine de traitement des données à câblage fixe[148].
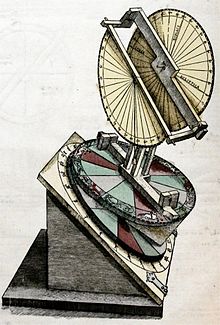
- Torquetum
Geber (vers 1100-1150) inventa le torquetum, à la fois instrument d’observation and calculateur analogique permettant de convertir les coordonnées équatoriales[149]. Il permettait de relever la position des astres et de les convertir en trois système de coordonnées: horizontales, équatoriales, et écliptiques.
- Astrolabe mécanique à calendrier perpétuel
En 1235, Abi Bakr d’Ispahan fabriqua un astrolabe équipé d'un calendrier mobile à engrenages en s'inspirant du calendrier mécanique d’Abū Rayhān al-Bīrūnī[150]. L’astrolabe à engrenages d’Abi Bakr, qui met en œuvre un train réducteur, constitue la plus vieille machine à engrenages fonctionnelle encore intacte[151],[152]
- Plaque des conjonctions
Au XVe siècle, al-Kashi mit au point une Plaque des conjonctions, calculateur permettant de trouver la date des conjonctions planétaires[153], et d’effectuer des interpolations linéaires[154].
- Calculateur planétaire
Au XVe siècle, ce même al-Kashi proposa un calculateur planétaire mécanique qu’il appela « plaque à orbes », et qui permettait de résoudre graphiquement un certain nombre de problèmes relatifs aux orbites des planètes, dont la prédiction de la longitude vraie du Soleil, de la Lune[154] et des planètes en considérant les orbites comme elliptiques[155] ; les latitudes du Soleil, de la Lune et des planètes ; et l’écliptique du Soleil. Cet instrument comportait aussi une alidade et une règle[156].
Horloges astronomiques
Les Musulmans équipèrent leurs observatoires d’horloges astronomiques de haute précision[157].
- Horloges astronomiques à eau
Al-Jazari inventa de monumentales horloges astronomiques à eau qui animaient des effigies du Soleil, de la Lune et des étoiles. La plus grande horloge astronomique représentait le zodiaque et les orbites solaire et lunaire. Innovation supplémentaire, cette horloge comportait dans la partie supérieure d'un panneau une bielle permettant d’ouvrir une trappe toutes les heures[158].
- Horloges astronomiques à ressort
Taqi al-Din inventa la première horloge astronomique à ressorts, décrite dans un livre intitulé Les plus brillantes étoiles pour la construction d'horloges mécaniques (Al-Kawākib al-durriyya fī wadh' al-bankāmat al-dawriyya, 1556-1559)[159].
- Carillons mécaniques
Taqi al-Din inventa le premier carillon mécanique à heures fixes, décrite dans l'ouvrage cité précédemment. La sonnerie était déclenchée par une bille sur un cadran à roue[159].
- Horloges mécaniques d’observation
Taqi al-Din inventa aussi l’« horloge d’observation », qu'il décrit comme « une horloge mécanique à trois cadrans donnant les heures, les minutes, et les secondes. » C'était la première horloge à mesurer le temps en secondes, et il l'utilisa spécifiquement pour mesurer l’ascension droite des étoiles. On considère que c'est l’une des plus importantes innovations d'astronomie pratique du XVIe siècle, dans la mesure où les horloges précédentes n'étaient pas assez précises pour l'astronomie[111]. Il améliora encore cette horloge, comme il l’explique dans son Sidrat al-muntaha, en n'utilisant plus qu'un cadran pour indiquer les heures, minutes et secondes. Il décrit cette horloge d’observation comme « une horloge mécanique à cadran unique affichant les heures, minutes et secondes où nous avons divisé chaque minute en cinq secondes[160]. »
Cadrans
Les astronomes et ingénieurs musulmans inventèrent d'innombrables types de cadrans pour la mesure du temps, et pour calculer les heures des cinq prières.
- Cadrans solaires
Les musulmans apportèrent des contributions significatives à la théorie et la fabrication des cadrans solaires, dont le principe leur venait de leurs prédécesseurs indiens et grecs. Al-Khwarizmi composa des tables qui abrégèrent et facilitèrent considérablement la fabrication de ces instruments. Les cadrans solaires arabes pouvaient être utilisés tels quels n’importe où sur Terre. On en plaçait fréquemment au fronton des mosquées pour vérifier l'heure de la prière. L’un des plus beaux spécimens fut fabriqué au XIVe siècle par le muwaqqit (grand horloger) de la mosquée omeyyade de Damas, Ibn al-Shatir[161]. Les astronomes et ingénieurs musulmans furent les premiers à coucher par écrit des instructions sur la construction de cadrans solaires tant horizontaux que verticaux ou polaires[162].
Comme les anciens cadrans étaient des écrans à style avec des lignes horaires rectilignes, ils marquaient des heures inégales (appelées d’ailleurs « heures apparentes ») qui variaient avec les saisons, chaque jour étant divisé en douze segments égaux : de la sorte, les heures étaient plus courtes l’hiver et plus longues l’été. L’idée de marquer des heures d’égale durée quelle que soit la période l’année est une innovation due à al-Shatir en 1371, suggérée par les découverte en trigonométrie d’Albategnus. Déjà, Ibn al-Shatir savait que « un gnomon parallèle à l'axe de la Terre fait un cadran solaire dont les divisions horaires marquent des heures de durées égales tout au long de l’année ». Son cadran solaire est le plus vieux cadran à axe polaire encore intact. Ce concept est connu de l’Occident dès 1446[163],[164].
- Navicula de Venetiis
Il s’agit d’un cadran horaire universel inventé au IXe siècle à Bagdad. On l'utilisait pour la mesure exacte du temps avec le Soleil et les étoiles, et il pouvait servir sous n'importe quelle latitude[165] (c’est là son caractère « universel »). L’Europe le reçut à la Renaissance sous le nom de « Navicula de Venetiis[166] », et le considérait comme l'horloge la plus précise[167].
- Cadran-boussole
Au XIIIe siècle, Ibn al-Shatir inventa la boussole à cadran, une horloge combinant un cadran solaire universel et une boussole : il l’utilisait pour trouver l’heure des Salah[168].
Globes
 Une sphère armillaire.
Une sphère armillaire.
- Sphères armillaires
Une sphère armillaire s'utilise de la même façon qu'un globe. Il ne subsiste aucune sphère armillaire provenant des pays arabes, mais plusieurs traités ont été composés sur l’« instrument à bagues ».
 Miniature ottomane d'une sphère armillaire - XVIe.L’astrolabe sphérique fut inventé par des astronomes musulmans.
Miniature ottomane d'une sphère armillaire - XVIe.L’astrolabe sphérique fut inventé par des astronomes musulmans.
- Astrolabes sphériques
Les astrolabes sphériques sont apparus pour la première fois dans le monde arabe[169]. C'était une variante régionale de l’astrolabe et de la sphère armillaire des Grecs, dont seul un spécimen, daté du XIVe siècle, subsiste.
- Globes terrestres
Le premier globe de l’Ancien Monde fut fabriqué dans le monde arabe au cours du Moyen Âge[170], par des géographes et des astronomes musulmans actifs sous le calife abbasside Al-Mamoun, au IXe siècle[171].
- Globes célestes
On utilisa d'abord les globes célestes pour résoudre les problèmes d'astronomie. Aujourd’hui, il subsiste 126 de ces appareils à travers le monde, dont le plus ancien remonte au XIe siècle. À l'aide de cet appareil, on pouvait déterminer la hauteur du Soleil, ou l’ascension droite et la déclinaison des étoiles en marquant la position de l’observateur le long de l'anneau méridien du globe.
Au XIIe siècle, Geber fut « le premier à concevoir une sphère céleste portative pour mesurer et expliquer les mouvements des astres[172]. »
- Les globes célestes d’une seule pièce
Les globes célestes d’une seule pièce fabriqués par des artisans de l’Empire moghol (à Lahore et dans le Cachemire), sont considérés comme l’un des plus hauts faits de métallurgie et d’artisanat de l’époque moderne. Tous les autres globes connus sont fabriqués par soudure de plusieurs éléments, et encore au XXe siècle, les métallurgistes considéraient qu’il était impossible de faire un globe de métal sans aucun pli de soudure. Mais dans les années 1980, l’archéologue Émilie Savage-Smith découvrit à Lahore et dans le Cachemire plusieurs globes de métal sans soudure. Le plus ancien a été construit au Cachemire par l’orfèvre Ali Kashmiri ibn Luqman en l'an 1589 sous le règne d’Akbar le Grand ; un autre, coulé en l'an 1659 par Muhammad Salih Tahtawi, porte des inscriptions en arabe et en sanskrit ; un troisième a été coulé à Lahore par l'orfèvre hindou Lala Balhumal Lahuri en 1842 sous le règne de Jagatjit Singh Bahadur. Il existe vingt-et-un autres globes de ce genre. Ces orfèvres du moghol avaient su développer une technique de coulée à la cire perdue pour atteindre ce résultat[173],[174].
Ces globes célestes d’une seule pièce sont sans équivalent : un auteur[174] n’hésite pas à comparer cette prouesse à ce que peut représenter la pyramide de Khéops pour l'architecture.
Théodolites muraux
Les astronomes et ingénieurs musulmans mirent au point toute une variété d’instruments de visée muraux (quadrants et sextants).
- quadrant à sinus
Le quadrant à sinus, inventé par Al-Khawarizmi dans le Bagdad du IXe siècle, servait aux calculs astronomiques[175].
- Quadrant horaire
Le premier quadrant horaire qui ne servait que sous certaines latitudes, fut imaginé par Al-Khawarizmi dans la Bagdad du IXe siècle, alors le centre de production de ces instruments[175]. On l'utilisait pour trouver l'heure (surtout les heures des prières) en observant le Soleil et les étoiles[176].
- Quadrans Vetus
Le Quadrans Vetus (« vieux quadrant », tel qu'on l’appelait en Europe lorsqu'on le connut, au XIIIe siècle) était un quadrant à temps universel. Cet appareil mathématique ingénieux avait lui aussi été imaginé par Al-Khawarizmi dans le Bagdad du IXe siècle. On pouvait l'utiliser sous n'importe quelle latitude et à n'importe quel moment de l'année pour trouver l'heure à partir de l’altitude du Soleil. C'est, derrière l’astrolabe, le deuxième instrument astronomique le plus répandu au Moyen Âge. Sa principale utilisation dans le monde musulman était le calcul des heures de la Salah[175].
- Le Quadrans Novus
Ce quadrant–astrolabe, que l’Europe a appelé Quadrans Novus (« quadrant moderne ») est apparu en Égypte au XIe siècle ou au XIIe siècle[177].
- Quadrant à almucantarat
Le premier quadrant à almucantarat est né dans le monde musulman, et se fondait sur les relations de trigonométrie. Le mot « almucantarat » lui-même vient de l'arabe[178]. Le quadrant à almucantarat n'est au départ qu'un astrolabe amélioré[162].
- Sextant
Le premier sextant, fabriqué à Ray (Teheran), est l’œuvre d’Abu-Mahmud al-Khujandi en 994. Il décrit cet instrument, permettant une très grande précision dans les mesures astronomiques, dans son traité, Sur l’inclinaison de l’écliptique et les latitudes des villes[179]. Au XVe siècle, Ulugh Beg fit construire le « Sextant de Fakhri », d’un rayon d’à peu près 36 m. Il se dressait à Samarkande, en Ouzbékistan, et cet arc édifié avec beaucoup de soin comportait des escaliers de chaque côté pour permettre aux assistants chargés des mesures de se déplacer rapidement.
Optique instrumentale
- Diaphragme
On trouve la première référence à un « tube d’observation » dans l’œuvre d’Albatenius (853-929), et la première description exacte d’un tel tube est due à al-Biruni (973-1048), dans une partie de son livre « consacrée à la vérification de la présence du croissant nouveau sur l’horizon. » Bien que ces diaphragmes primitifs soient encore dépourvus de lentille optique, ils « permettaient à l'observateur de se concentrer sur une zone du ciel en éliminant les interférences de la lumière. » Ces tubes furent adoptés plus tard dans l’Europe latine, où ils influencèrent le développement de la lunette astronomique[180].
- Appareil expérimental à diaphragmes
Pour prouver que « de la lumière est émise de chaque point de la surface éclairée de la Lune », Alhazen fabriqua « un appareil ingenieux » montrant « que l’intensité de la tache de lumière formée sur un écran par la projection de la clarté lunaire à travers deux petites ouvertures diminue constamment à mesure que l’on obture l’un des trous[47]. »
- Lentilles de verre
Le premier travail d’optique décrivant une loupe intégrée à un instrument est le Traité d’Optique (1021) composé par Alhazen[181]. Ses descriptions furent reprises en Europe lors des premières recherches sur la réfraction[182] ; quant à ses autres travaux sur la réfraction, les miroirs paraboliques, et ses autres instruments comme la chambre noire, jouèrent également leur rôle dans la Révolution mécaniste[181],[183].
- Anticipation supposée du principe de la lunette astronomique
Taqi al-Din imagina un « appareil pour voir à longue distance », comme il l'affirme dans son Livre de la Lumière de la pupille et de la Vérité des images de 1574 ; il a pu s'agir d'une lunette astronomique primitive : il dit que cet instrument fait apparaître les objets éloignés plus près qu'il ne sont, et qu'il permet de voir les détails d'objets éloignés. Taqi al-Din affirme qu'il a écrit un autre traité (perdu aujourd'hui) où il explique la fabrication et l’utilisation de cet instrument. Ce qu'il décrit est cependant confus car il ajoute que son appareil est semblable à celui qu’utilisaient les Grecs au Pharos d’Alexandrie[112].
Autres instruments
D'autres instruments astronomiques ont vu le jour dans le monde arabe :
- boussole astronomique: la première utilisation d’une boussole à aiguille aimantée est évoquée dans un traité sur les instruments astronomiques dû à la plume du sultan yéménite al-Ashraf (†1296) en 1282[184].
- boussole sèche : en 1282, al-Ashraf fit construire une boussole améliorée comme « index à Qibla », c'est-à-dire pour trouver la direction de La Mecque. L’instrument d’Al-Ashraf est l'une des plus anciennes boussoles sèches, et il semble que Pierre de Maricourt ait fait simultanément cette découverte[185]
Une alidade.
- Alidade: l’alidade, mot d'étymologie arabe, est apparue dans le monde musulman.
- Compendium: il s’agit d’un instrument polyvalent, dont le premier exemple est décrit par l'astronome Ibn al-Shatir au XIIIe siècle. Son compendium consistait entre autres en une alidade et un cadran solaire de type polaire. Al-Wafa'i réalisa au XVe siècle un autre compendium qu'il appela « cercle équatorial », et qui comportait également un cadran solaire horizontal. Ces compendia furent par la suite très répandus dans l’Europe de la Renaissance[162].
- Cadrans à réseau orthogonal : les quadrants arabes utilisés dès le Xe siècle tant pour l’astronomie que comme horloges, comportaient une grille régulière à réseau orthogonal, avec des graduations semblables à celles de notre Papier millimétré[186],[187].
- sextant à réseau : entre 1577 et 1580, Taqi al-Din, à l’observatoire d'Istanbul, inventa un sextant à réseau (mushabbaha bi'l manattiq), muni de cordelettes pour déterminer les équinoxes ; Tycho Brahe utilisa un appareil similaire par la suite[111].
- Index à qibla: dans la Perse séfévide du XVIIe siècle, deux instruments en bronze uniques comportant, gravées, des cartes du monde centrées sur La Mecque, servaient essentiellement à trouver la qibla. Sur le plateau de ces instruments, un canevas cartographique était gravé, qui permettait de trouver la direction et la distance à La Mecque depuis n'importe quel point de la Terre. De tels canevas cartographiques peuvent remonter à la Bagdad du Xe siècle[167]. À l’un des deux instruments, fabriqué par Muhammad Husayn[188], étaient attachés un cadran solaire et une boussole[189].
- Carré à ombre: cet instrument, muni d'une alidade, servait à trouver la taille en hauteur d'un objet, pour les mesures d'angle[190]. Son invention est due à Al-Khawarizmi au IXe siècle à Bagdad[191].
Traités célèbres
Les tables numériques (« Zij »)
Article détaillé : Zij.- Ibrahim al-Fazari († 777) et Mohamed al-Fazari (d. 796/806)
- Az-Zij ‛alā Sinī al-‛Arab (vers 750)
- Yaqub ibn Tariq († 796)
- Az-Zij al-Mahlul min as-Sindhind li-Darajat Daraja
- Al-Khawarizmi (latinisé en Algorismus) (vers 780-850)
- Zij al-Sindhind (vers 830)
- Al-Battani (latinisé en Albategnus) (853-929)
- Az-Zij as-Sabi
- Al-Soufi (latinisé en Azophus) (903 † 986)
- Livre des Fixes (vers 964)
- Ibn Younous (vers 950-1009)
- Zij al-Kabir al-Hakimi
- Al-Zarqali (latinisé en Arzachel) (1028-1087)
- Al-Khazini (fl. 1115-1130)
- Az-Zij as-Sanjarī (Tables de Sinjar) (1115-1116)
- Nasir ad-Din at-Tusi (1201-1274)
- Zij-i Ilkhani (Tables d’Ilkhan) (1272)
- Al-Kachi (1380-1429)
- Khaqani Zij
- Ulugh Beg (1394-1449)
- Tables sultaniennes (1437)
- Taqi al-Din (1526-1585)
- La perle intacte (1577-1580)
Almanachs
Le mot « almanach » est d’étymologie arabe[192]. L’almanach diffère des tables astronomiques antérieures (comme par exemple les tables babyloniennes, ptolémaïques et les tables Zij) en ceci que « les lignes d'un almanach donnent directement les positions des astres et ne demandent aucun calcul supplémentaire », au contraire des « tables auxiliaires » habituelles fondées sur l’Almageste de Ptolémée. Le plus vieil almanach connu (au sens moderne) est l’Almanach d’Azarchel composé en 1087 par Al-Zarqali à Tolède, dans le royaume d’al-Andalus. Ces tables donnaient pour chaque jour les positions vraies du Soleil, de la Lune et des planètes pour les quatre années allant de 1088 à 1092, ainsi que plusieurs autres tables. Une traduction latine de cet ouvrage fut publiée sous le titre de Tables de Tolède au XIIe siècle et les tables alphonsines en sont une adaptation du XIIIe siècle[193].
Traités sur les instruments
Au XIIe siècle, al-Khazini écrivit le Risala fi'l-alat (Traité sur les instruments) en sept parties qui décrit différents instruments scientifiques : le triquetrum, la dioptre, un instrument triangulaire de son invention, le quadrant et le sextant, l’astrolabe, et divers instruments à miroirs originaux[194].
Dans l’Égypte du XIVe siècle, Najm al-Din al-Misri (vers 1325) composa un traité décrivant plus de 100 types différents d’instruments scientifiques et astronomiques, la plupart de son invention[167].
En 1416, al-Kashi écrivit le Traité sur les instruments d’observation astronomiques, qui décrit une multitude d’instruments différents, dont le triquetrum et la sphère armillaire, l’armillaire équinoxiale et solstitielle de Mo'ayyeduddin Urdi, l’instrument aux sinus et aux sinus verse d’Urdi, le sextant d’al-Khujandi, le sextant de Fakhri à l’observatoire de Samarkande, un double quadrant Azimuth-altitude, et une petite sphère armillaire munie d'une alidade de son invention[195].
Autres ouvrages
- Mohammed Ben Musa (800-873)
- Livre sur le mouvement des orbes
- Mouvement astral
- La Force d’attraction
- Alfraganus (†850)
- Éléments d’astronomie sur les mouvements célestes (vers 833)
- Kitab fi Jawami Ilm al-Nujum
- Alhazen (965-1039)
- De la Figure du Monde
- Doutes sur Ptolémée (vers 1028)
- Les Doutes levés (vers 1029)
- Modèle du mouvement des sept planètes (1029-1039)
- al-Biruni (973-1048)
- Kitab al-Qanun al-Mas'udi (Le canon Mas'udi) (1031)
- Al-Juzjani (vers 1070)
- Tarik al-Aflak (1070)
- Al-Istidrak ala Batlamyus (Récapitulation à propos de Ptolémée) (XIe siècle)
- Al-Khazini (fl. 1115-1130)
- Risala fi'l-alat (Traité sur les instruments)
- Nasir ad-Din at-Tusi (1201-1274)
- Al-Tadhkirah fi'ilm al-hay'ah (Aide-mémoire d’astronomie)
- 'Umar al-Katibi al-Qazwini († 1277)
- Hikmat al-'Ain
- Qutb al-Din al-Shirazi (1236 † 1311)
- Le summum de la connaissance des cieux
- Ibn al-Shatir (1304–1375)
- Ultime recherche sur la correction de la théorique des planètes
- Ali Qushji († 1474)
- Du caractère prétendûment subalterne de l’Astronomie par rapport à la Philosophie
- Shams al-Din al-Khafri († 1525)
- Complément à l'explication de l’Aide-mémoire
Noms d'étoiles d'origine arabe
Bien[Combien ?] des noms modernes d'étoiles et de constellations sont d’étymologie arabe. Ainsi par exemple : Acamar (θ Eridani), Aldébaran (α Tauri), Algol (β Persei, Altaïr (α Aquilae), Baham (θ Pegasi), Baten Kaitos (ζ Ceti), Caph (β Cassiopeiae), Dabih (β Capricorni), Edasich (ι Draconis), Furud (ζ Canis Majoris), Gienah (γ Corvi et ε Cygni), Hadar (β Centauri), Izar (ε Bootis), Jabbah (ν Scorpii), Keid (40 Eridani), Lesath (ν Scorpii et υ Scorpii), Mirak (au moins trois étoiles), Phad (α Columbae et γ Ursae Majoris), Rigel (β Orionis), Sadr (γ Cygni), Altarf (β Cancri, et Vega (α Lyrae), parmi bien d'autres (voir Liste de noms traditionnels d'étoiles). Certains de ces noms étaient déjà attribués au temps de l’Arabie Heureuse, mais beaucoup ne furent donnés que par la suite, comme des traductions de descriptions en grec ancien[196].
Notes et références
- (Gingerich 1986)
- Virendra Nath Sharma, Sawai Jai Singh and His Astronomy, Motilal Banarsidass Publ., 1995, 8–10 p. (ISBN 8120812565)
- (Saliba 1999)
- Benno van Dalen et S. M. Razaullah Ansari (dir.), History of Oriental Astronomy, Islamic Astronomical Tables in China: The Sources for Huihui li, Springer Verlag, 2002, 19–32 p. (ISBN 1402006578)
- Arabic Star Names, Islamic Crescents' Observation Project, 2007-05-01. Consulté le 2008-01-24
- Mohammad Ilyas, Islamic Astronomy, Pelanduk Publications, 1997 (ISBN 9-67978-549-1)
- Le Coran, « Le Bétail », VI, 97 ; (ar) الأنعام
- I. A. Ahmad, « The impact of the Qur'anic conception of astronomical phenomena on Islamic civilization », dans Vistas in Astronomy, vol. 39, no 4, 1995, p. 395–403
- I. A. Ahmad, The Rise and Fall of Islamic Science: The Calendar as a Case Study, Faith and Reason: Convergence and Complementarity, Université d'Al Akhawayn, 3 juin 2002, PDF [lire en ligne (page consultée le 2008-01-31)]
- Le Coran, « Les Prophètes », XXI, 30 ; (ar) الأنبياء
- Le Coran, « Qui éparpillent », LI, 47 ; (ar) الذاريات
- Le Coran, « Noé », LXXI, 14 ; (ar) نوح
- James A. Michene, « Islam: The Misunderstood Religion », dans Reader's Digest, mai 1955, p. 68–70
- Le Coran, « L’Immunité ou le Repentir », IX, 36 ; (ar) التوبة
- Le Coran, « La Vache », II, 185 ; (ar) البقرة
- Syed Mohammad Hussain Tabatabai, Tafsir al-Mizan, vol. 3 : Surah Baqarah, Verse 189 [lire en ligne (page consultée le 24 janvier 2008)]
- Khalid Shaukat, « The Science of Moon Sighting », 23 septembre 1997. Consulté le 24 janvier 2008
- Le Coran, « La Vache », II, 144 ; (ar) البقرة
- Le Coran, « La Vache », II, 150 ; (ar) البقرة
- Syed Mohammad Hussain Tabatabai, Tafsir al-Mizan, vol. 2 : Surah Baqarah, Versets 142-151 [lire en ligne (page consultée le 24 janvier 2008)]
- Cf. Dallal (1999), p=162.
- What is the Hijrah Calendar?
- Ce livre ne doit pas être confondu avec celui d’Al-Khawarizmi, intitulé exactement Zij al-Sindh. Sur les tables numériques (zijes), cf. (Kennedy 1956)
- (King 2002, p. 240)
- (par opposition à la Petite astronomie, qui regroupait plusieurs auteurs : la sphère en mouvement d’Autolycos de Pitane, les Sphériques de Théodose, etc. Cf. à ce sujet P. ver Eecke, intr. aux Sphériques de Théodose, Paris, Blanchard.
- Greek Astronomy. Consulté le 2008-01-15
- Almagest, The Internet Encyclopedia of Science. Consulté le 15 janvier 2008
- (en) John J. O’Connor et Edmund F. Robertson, « Abu Said Sinan ibn Thabit ibn Qurra », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne (page consultée le 2008-01-15)].
- (Dallal 1999, p. 163)
- (Dallal 1999, p. 164)
- (Singer 1959, p. 151) (cf. (Zaimeche 2002))
- (Wickens 1976) (cf. (Zaimeche 2002))
- 23rd Annual Conference on the History of Arabic Science, Alep, Syrie, octobre 2001 (cf. (Zaimeche 2002))
- George Robert Kepple, The Night Sky Observer's Guide, vol. 1, Willmann-Bell, Inc., 1998 (ISBN 0-943396-58-1)
- Observatoire de Paris (Abd-al-Rahman Al Sufi). Consulté le 2007-04-19
- Observatoire de Paris (LMC). Consulté le 2007-04-19
- (Zaimeche 2002)
- Richard P. Aulie, « Al-Ghazali Contra Aristotle: An Unforeseen Overture to Science In Eleventh-Century Baghdad », dans Perpectives on Science and Christian Faith, vol. 45, mars 1994, p. 26–46 (cf. References, 1001 Inventions. Consulté le 2008-01-22)
- Cf. Bartel Leendert van der Waerden, « The Heliocentric System in Greek, Persian and Hindu Astronomy », dans Annals of the New York Academy of Sciences, vol. 1, no 500, 1987, p. 525–545 [534-537] qui nous les ont transmises.
- (Nasr 1993)
- William Lane Craig, « Whitrow and Popper on the Impossibility of an Infinite Past », dans The British Journal for the Philosophy of Science, vol. 30, no 2, June 1979, p. 165–170 [165–6]
- (Saliba 1994a, p. 116)
- K. A. Waheed, Islam and The Origins of Modern Science, Lahore, Islamic Publication Ltd., 1978
- (Briffault 1938, p. 191)
- (Huff 2003, p. 57)
- (Huff 2003, p. 326)
- G. J. Toomer, « Review: Ibn al-Haythams Weg zur Physik by Matthias Schramm », dans Isis, vol. 55, no 4, décembre 1964, p. 463–465 [463–4] [lien DOI]
- (Rosen 1985)
- Josep Puig Montada, « Ibn Bajja », Stanford Encyclopedia of Philosophy, September 28, 2007. Consulté le 11 juillet 2008
- Mohaini Mohamed, Great Muslim Mathematicians, Penerbit UTM, 2000, 49–50 p. (ISBN 9835201579)
- Hamid-Eddine Bouali, Mourad Zghal, Zohra Ben Lakhdar, « Popularisation of Optical Phenomena: Establishing the First Ibn Al-Haytham Workshop on Photography », The Education and Training in Optics and Photonics Conference, 2005. Consulté le 2008-07-08
- Dr. A. Zahoor, « Abu Raihan Muhammad al-Biruni », Hasanuddin University, 1997
- Abu Rayhan Muhammad ibn Ahmad al-Biruni, MacTutor Biography
- (Sabra 1998)
- Dennis Duke, « Arabic Models for outer Planets and Venus ». Consulté le 2008-01-22
- (Sabra 1998)
- (Ragep, Teresi et Hart 2002)
- Cf. S. Pines, « The Semantic Distinction between the Terms Astronomy and Astrology according to al-Biruni », dans Isis, vol. 3, no 55, septembre 1964, p. 343-349.
- (Saliba 1994b)
- John W. Livingston, « Ibn Qayyim al-Jawziyyah: A Fourteenth Century Defense against Astrological Divination and Alchemical Transmutation », dans Journal of the American Oriental Society, vol. 91, no 1, 1971, p. 96–103
- John W. Livingston, « Ibn Qayyim al-Jawziyyah: A Fourteenth Century Defense against Astrological Divination and Alchemical Transmutation », dans Journal of the American Oriental Society, vol. 91, no 1, 1971, p. 96–103 [99]
- Khwarizm, Foundation for Science Technology and Civilisation. Consulté le 22 janvier 2008
- (Iqbal et Berjak 2003)
- (Zaimeche 2002, p. 7)
- (Sabra 1998, p. 300)
- Stanford Encyclopedia of Philosophy, 2004 [lire en ligne (page consultée le 22 janvier 2008)], « Nicolaus Copernicus »
- (Langermann 1990)
- (Duhem 1969, p. 28)
- (Marshall 1950)
- (Rashed 2007)
- (Rashed 2007)
- (Rashed 2007)
- (Rashed 2007)
- (Rashed 2007)
- (Rashed 2007)
- (Nasr 1993, p. 135, n. 13)
- (Baker et Chapter 2002)
- (Marmura 1965)
- D'après G. Wiet, V. Elisseeff, P. Wolff, J. Naudu, History of Mankind, vol. 3 : The Great medieval Civilisations, UNESCO, George Allen & Unwin Ltd, 1975, p. 649.
- (Covington 2007)
- (Nasr 1993, p. 134)
- (Saliba 1980, p. 249)
- (Sabra 1998)
- (Saliba 1981, p. 219)
- Pour davantage de précisions, cf. A. I. Sabra et =Everett Mendelsohn (dir.), The Andalusian Revolt Against Ptolemaic Astronomy: Averroes and al-Bitrûjî, Transformation and Tradition in the Sciences: Essays in honor of I. Bernard Cohen, Cambridge University Press, 233–53 p..
- Robert Briffault (1938). The Making of Humanity, p. 190.
- «L’épicycle et l’excentrique sont impossibles. Il est donc nécessaire de se livrer à de nouvelles recherches au sujet de cette astronomie véritable dont les fondements sont des principes de Physique» Averroès, Métaphysique, Liv. XII, part. II, chap. 4, com. 45.
- D’après Bernard R. Goldstein, « Theory and Observation in Medieval Astronomy », dans Isis, vol. 1, no 63, mars 1972, p. 39-47 [40-41].
- Bernard R. Goldstein, « Theory and Observation in Medieval Astronomy », dans Isis, vol. 1, no 63, mars 1972, p. 39-47 [41].
- Ptolemaic Astronomy, Islamic Planetary Theory, and Copernicus's Debt to the Maragha School, Science and Its Times, Thomson Gale, 2005-2006 [lire en ligne (page consultée le 22 janvier 2008)]
- Cf. Saliba (1994b), pp=233-234 & 240.
- Cf. Dallal (1999), p=171.
- (Saliba 1994b)
- George George Saliba, « Seeking the Origins of Modern Science? », dans BRIIFS, vol. 1, no 2, automne 1999 [texte intégral (page consultée le 25 janvier 2008)]
- (Saliba 1994b)
- Ahmad Dallal, The Interplay of Science and Theology in the Fourteenth-century Kalam, From Medieval to Modern in the Islamic World, coll. « Sawyer Seminar at the University of Chicago », 2001-2002 [lire en ligne (page consultée le 2 février 2008)]
- (Huff 2003)
- (Ragep 2001a)
- (Ragep 2001b)
- (Saliba 1994b)
- (Saliba 1979)
- (Gill 2005)
- Y. M. Faruqi, « Contributions of Islamic scholars to the scientific enterprise », dans International Education Journal, vol. 4, no 7, 2006, p. 395-396.
- D'après Richard Bulliet, Pamela Crossley, Daniel Headrick, Steven Hirsch, Lyman Johnson, and David Northrup, The Earth and Its Peoples, vol. 3, Boston, Houghton Mifflin Co., 2005 (ISBN 0-618-42770-8).
- Siben Zhu, The « Mongol Atlas » of China, Taipei, Université catholique Fu-Jen, 1946.
- (Saliba 2000)
- Edith Dudley Sylla et Arthur Stephen McGrade (dir.), Creation and nature, Cambridge University Press, 2003, 178-179 p. (ISBN 0521000637).
- (Ragep 2001b)
- (Ragep 2001a)
- George Saliba, Roshdi Rashed (dir.) et Régis Morelon (dir.), Arabic planetary theories after the eleventh century AD, Histoire des sciences arabes, éditions du Seuil, 1997, 3 vol. brochés 17 × 22 cm x 4 cm (ISBN 2-02030-352-3), p. 58-127
- Cf. Sevim Tekeli et Helaine Selin (dir.), Taqi al-Din, Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Kluwer Academic Publishers, 1997 (ISBN 0792340663).
- Hüseyin Gazi Topdemir, Takîyüddîn'in Optik Kitabi, Ankara, Ministère de la Culture, 1999 (cf. Dr. Hüseyin Gazi Topdemir, « Taqi al-Din ibn Ma‘ruf and the Science of Optics: The Nature of Light and the Mechanism of Vision », FSTC Limited, 30 juin 2008. Consulté le 4 juillet 2008).
- Avner Ben Zaken, « The heavens of the sky and the heavens of the heart: the Ottoman cultural context for the introduction of post-Copernican astronomy », dans The British Journal for the History of Science, Cambridge University Press, vol. 37, 2004, p. 1–28
- Virendra Nath Sharma, Sawai Jai Singh and His Astronomy, Motilal Banarsidass Publ., 1995 (ISBN 8120812565), p. 8–9
- Zaheer Baber, The Science of Empire: Scientific Knowledge, Civilization, and Colonial Rule in India, State University of New York Press, 1996 (ISBN 0791429199), p. 82–9
- Zaheer Baber, The Science of Empire: Scientific Knowledge, Civilization, and Colonial Rule in India, State University of New York Press, 1996 (ISBN 0791429199), p. 89–90
- Peter Bond, « Obituary: Lt-Gen Kerim Kerimov », dans The Independent, 7 avril 2003 [texte intégral (page consultée le 22 janvier 2008)]
- Betty Blair, « Behind Soviet Aeronauts », dans Azerbaijan International, vol. 3, no 3, 1995
- Muslim Scientists and Space Exploration - Farouk El-Baz: With Apollo to the Moon - Interview, IslamOnline. Consulté le 15 janvier 2008
- The Star, « Mission in space », The Star, 13 octobre 2007
- Muslim Scientists and Space Exploration - Essam Heggy: Into the Heart of Mars - Interview, IslamOnline. Consulté le 15 janvier 2008
- Farnaz Fassihi, « Muslim Moon Hunting Evolves », dans The Wall Street Journal, 15 octobre 2007, p. A8 [texte intégral (page consultée le 24 janvier 2008)]
- Moon Sighting. Consulté le 24 janvier 2008
- Hilal-Sighting, Columbia University, New York. Consulté le 24 janvier 2008
- Islamic crescent's observation project. Consulté le 24 janvier 2008
- Huda, « Moon-Sighting at Ramadan ». Consulté le 24 janvier 2008
- Fasting month of Ramadan begins in Qatar today, 23 septembre 2006. Consulté le 24 janvier 2008
- A New World Record for Lunar Crescent Sighting By Mr. Mohsen G. Mirsaeed, Islamic Crescents' Observation Project. Consulté le 24 janvier 2008
- (Kennedy 1962)
- Francoise Micheau, Rashed (dir.) et Morelon (dir.), The Scientific Institutions in the Medieval Near East, Histoire des sciences arabes, 1997, p. 992–3
- Prof. Osman Bakar (Georgetown University), Islam's Contribution to Human Civilization: Science and Culture, CIC's annual Ottawa dinner, 15 octobre 2001 [lire en ligne (page consultée le 22 janvier 2008)]
- (en) John J. O’Connor et Edmund F. Robertson, « Abu Mahmud Hamid ibn al-Khidr Al-Khujandi », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne].
- Jordanian Astronomical Society. Consulté le 2008-01-15
- Palestinian Astronomical Society. Consulté le 15 janvier 2008
- Lebanese Astronomical society. Consulté le 15 janvier 2008
- Emirates Astronomical Society. Consulté le 15 janvier 2008
- Société Astronomique de Tunise. Consulté le 15 janvier 2008
- Feder Toni, « Iran Invests in Astronomy », Physics Today, juillet 2004. Consulté le 22 janvier 2008
- Cf. (en) Richard Nelson Frye, Golden Age of Persia, Orion Publ., 2000, p. 163.
- Emily Winterburn (National Maritime Museum), « Using an Astrolabe », Foundation for Science Technology and Civilisation, 2005. Consulté le 22 janvier 2008
- Islam, Knowledge, and Science, Université de la Californie méridionale. Consulté le 22 janvier 2008
- Cf. Robert Hannah, « The Mapping of the Heavens by Peter Whitfield », dans Imago Mundi, no 49, 1997, p. 161-162.
- Linear astrolabe, Encyclopædia Britannica, 2007 [lire en ligne (page consultée le 22 janvier 2008)]
- (King 1983)
- (Hassan)
- Will Durant, The Story of Civilization, vol. IV : The Age of Faith, 1950, p. 239-45.
- (Hill 1985)
- Tuncer Oren, « Advances in Computer and Information Sciences: From Abacus to Holonic Agents », dans Turk J Elec Engin, vol. 1, no 9, 2001, p. 63-70 [64].
- R. P. Lorch, « The Astronomical Instruments of Jabir ibn Aflah and the Torquetum », dans Centaurus, vol. 20, no 1, 1976, p. 11–34
- « Mechanical Universe: The Astrarium of Giovanni de’ Dondi », dans Transactions of the American Philosophical Society, no 56, 1966, p. 1-69.
- Astrolabe gearing, Museum of the History of Science (Oxford), 2005. Consulté le 22 janvier 2008
- History of the Astrolabe, Museum of the History of Science (Oxford)
- (Kennedy 1947, p. 56)
- (Kennedy 1950)
- (Kennedy 1952)
- (Kennedy 1951)
- (Ajram 1992)
- (Hill 1991)
- Salim Al-Hassani, « The Astronomical Clock of Taqi Al-Din: Virtual Reconstruction », FSTC, 19 juin 2008. Consulté le 2 juillet 2008
- Aydin Sayili, The Observatory in Islam, 1991, 289–305 p. (cf. Dr. Salim Ayduz, « Taqi al-Din Ibn Ma’ruf: A Bio-Bibliographical Essay », 26 juin 2008. Consulté le 2008-07-04)
- (King 1999a)
- David A. King, R. Rashed (dir.) et R. Morelon (dir.), Astronomy and Islamic society, Histoire des sciences arabes, Seuil, 1997, broché 17 × 22 cm x 4 cm, 163–8 p.
- History of the sundial, National Maritime Museum. Consulté le 2008-07-02
- Lawrence Jones, « The Sundial And Geometry », dans North American Sundial Society, vol. 12, no 4, décembre 2005
- (King 2005)
- (King 2003)
- (King 2004)
- (King 1983)
- Emilie Savage-Smith (1993). "Book Reviews", Journal of Islamic Studies 4 (2): 296-299. « Tandis qu'il n'y a aucune preuve sur l’origine hellénistique de l’astrolabe sphérique, toutes les sources connues renvoient à un développement ancien mais clairement arabe. »
- Mark Silverberg. Origins of Islamic Intolerence.
- Erreur dans la syntaxe du modèle ArticleRichard Covington, « {{{title}}} », dans Saudi Aramco World, 2007, p. 17–21 [texte intégral (page consultée le 6 juillet 2008)]
- An overview of Muslim Astronomers, FSTC Limited, 26 December 2001. Consulté le 2008-02-01
- Emilie Savage-Smith, Islamicate Celestial Globes: Their History, Construction, and Use, Washington, D.C., Smithsonian Institution Press, 1985
- Najma Kazi, « Seeking Seamless Scientific Wonders: Review of Emilie Savage-Smith's Work », FSTC Limited, 24 novembre 2007. Consulté le 1er février 2008
- (King 2002)
- (King 1999a)
- (King, Cleempoel et Moreno 2002, p. 333)
- Cf. Noël Tardy, Astrolabes, cartes du ciel – les comprendre et les construire, Edisud, 144 p. (ISBN 2-7449-0078-8), p. 12 ; Elly Dekker, « An unrecorded medieval astrolabe quadrant from c. 1300 », dans Ann. Sci., vol. 1, no 52, 1995, p. 1-47 [6].
- [www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/Al-Khujandi.html Al-Khujandi]
- Regis Morelon (dir.) et Morelon (dir.), General Survey of Arabic Astronomy, Histoire de la science arabe, 1996, p. 1-19
- A. I. Sabra & J. P. Hogendijk, The Enterprise of Science in Islam: New Perspectives, MIT Press, 2003 (ISBN 0262194821), p. 85-118
- Cf. Bernard Maitte, La lumière, vol. S28, éditions du Seuil, coll. « Points sciences », 346 p., p. 34 et 71 ; O. S. Marshall, Alhazen and the Telescope, Astronomical Society of the Pacific Leaflets 6, 1950, p. 4
- Richard Powers (University of Illinois), « Best Idea; Eyes Wide Open », dans New York Times, 18 avril 1999.
- Emilie Savage-Smith, « Gleanings from an Arabist's Workshop: Current Trends in the Study of Medieval Islamic Science and Medicine », dans Isis, vol. 2, no 79, 1988, p. 246-266 [263].
- Petra G. Schmidl, « Two Early Arabic Sources On The Magnetic Compass », dans Journal of Arabic and Islamic Studies, vol. 1, 1996-1997, p. 81–132
- Josef W. Meri et Taylor and Francis (dir.), Medieval Islamic Civilization: An Encyclopedia, 2006 (ISBN 0415966914), p. 75.
- (King 1999b, p. 17)
- (Iqbal 2003)
- (King 1997, p. 62)
- Shadow square, National Maritime Museum. Consulté le 22 janvier 2008
- (King 2002)
- (Glick, Livesey et Wallis 2005, p. 29)
- (Glick, Livesey et Wallis 2005, p. 30)
- Robert E. Hall (1973). "Al-Biruni", Dictionary of Scientific Biography, Vol. VII, p. 338.
- (Kennedy 1961)
- Cf. (en) Arabic Star names
Voir aussi
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Astronomy in medieval Islam » (voir la liste des auteurs)
Bibliographie
- En français
- Roshdi Rashed (dir.) et Régis Morelon (dir.), Histoire des sciences arabes, vol. I (376 p.) : Astronomie, théorique et appliquée, Paris, éditions du Seuil, 1997, 3 vol. (ISBN 2-02030-352-3)
- Abdulhak Adnan, La science chez les Turcs ottomans, Paris, Maisonneuve, 1939, 82 p.
- Pierre Duhem, Sozein ta phainomena. Essai sur la notion de théorie physique de Platon à Galilée, Vrin, coll. « Mathesis », 1908 (réimpr. 1992) (ISBN 2-71160-805-0)
- Antoine Gautier, L’âge d'or de l’astronomie ottomane, vol. 119 : L’Astronomie (mensuel fondé par Camille Flammarion en 1882), décembre 2005
- Paul Couderc, Histoire de l'astronomie, vol. 165, Presses universitaires de France, coll. « Que sais-je ? », 1945 (réimpr. 6e éd. 1974)
Un ouvrage de vulgarisation un peu daté, mais très clair et particulièrement agréable à (re-)lire.
- Jean-Pierre Verdet, Une histoire de l’astronomie, éditions du Seuil, coll. « Points sciences », 1990, 384 p. (ISBN 2-02-011557-3)
- Dans d'autres langues
- K. Ajram, Miracle of Islamic Science, Knowledge House Publishers (ISBN 0911119434), « Appendix B »
- A. Baker, L. Chapter et M. Sharif (dir.), 4. The Sciences, Philosophia Islamica, 2002, partie A History of Muslim Philosophy
- Robert Briffault, The Making of Humanity, 1938
- Richard Covington, Rediscovering Arabic science, Saudi Aramco World, May-June 2007, 2–16 p.
- Ahmad Dallal et John Esposito (dir.), Science, Medicine and Technology, The Oxford History of Islam, New York, Oxford University Press, 1999
- M. Gill, Was Muslim Astronomy the Harbinger of Copernicanism?, 2005 [lire en ligne (page consultée le 2008-01-22)]
- Owen Gingerich, Islamic astronomy, vol. 254, April 1986 [lire en ligne (page consultée le 2008-05-18)]
- Thomas F. Glick, Steven John Livesey et Faith Wallis, Medieval Science, Technology, and Medicine: An Encyclopedia, Routledge, 2005 (ISBN 0415969301)
- Ahmad Y. Hassan, Transfer Of Islamic Technology To The West, Part II: Transmission Of Islamic Engineering [lire en ligne (page consultée le 2008-01-22)]
- Donald R. Hill, « Al-Biruni's mechanical calendar », dans Ann. Sci., vol. 42, 1985, p. 139–163
- Donald R. Hill, Mechanical Engineering in the Medieval Near East, May 1991, 64–69 p. (cf. Donald R. Hill, Mechanical Engineering [lire en ligne (page consultée le 2008-01-22)])
- Donald R. Hill, Islamic Science And Engineering, Edinburgh University Press, 1993 (ISBN 0-7486-0455-3)
- Toby, The Rise of Early Modern Science: Islam, China, and the West, Cambridge University Press, 2003 (ISBN 0521529948)
- Mohammad, Islamic Astronomy, Pelanduk Publications, 1997 (ISBN 9679785491)
- Muzaffar Iqbal, « Review: World-Maps for Finding the Direction and Distance to Mecca: Innovation and Tradition in Islamic Science by David A. King », dans Islam & Science, 2003, juin 2003
- Muzaffar Iqbal,Rafik Berjak, « Ibn Sina–Al-Biruni correspondence », dans Islam & Science, 2003, juin
- Edward S. Kennedy, « Al-Kashi's Plate of Conjunctions », dans Isis, vol. 38, no 1-2, 1947, p. 56–59
- Edward S. Kennedy, « A Fifteenth-Century Planetary Computer: al-Kashi's "Tabaq al-Manateq" I. Motion of the Sun and Moon in Longitude », dans Isis, vol. 41, no 2, 1950, p. 180–183
- Edward S. Kennedy, « An Islamic Computer for Planetary Latitudes », dans Journal of the American Oriental Society, vol. 71, no 1, 1951, p. 13–21
- Edward S. Kennedy, « A Fifteenth-Century Planetary Computer: al-Kashi's "Tabaq al-Maneteq" II: Longitudes, Distances, and Equations of the Planets », dans Isis, vol. 43, no 1, 1952, p. 42–50
- Edward S. Kennedy, « A Survey of Islamic Astronomical Tables », dans Transactions of the American Philosophical Society, vol. 46, no 2, 1956
- Edward S. Kennedy, « Al-Kashi's Treatise on Astronomical Observational Instruments », dans Journal of Near Eastern Studies, vol. 20, no 2, 1961, p. 98–108
- Edward S. Kennedy, « Review: The Observatory in Islam and Its Place in the General History of the Observatory by Aydin Sayili », dans Isis, vol. 53, no 2, 1962, p. 237–239
- Edward S. Kennedy, Astronomy and Astrology in the Medieval Islamic World, Brookfield, VT: Ashgate, 1998
- David A. King, « The Astronomy of the Mamluks », dans Isis, vol. 74, no 4, 1983, p. 531–555
- David A. King, Islamic mathematical astronomy, Londres, 1986
- David A. King, « Two Iranian World Maps for Finding the Direction and Distance to Mecca », dans Imago Mundi, vol. 49, 1997, p. 62–82
- David A. King et Christopher Walker (dir.), Islamic Astronomy, Astronomy before the telescope, British Museum Press, 1999a, 143–174 p. (ISBN 0-7141-2733-7)
- King, World-maps for Finding the Direction and Distance to Mecca: Innovation and Tradition in Islamic Science, Brill Publishers, 1999b (ISBN 9004113673)
- David A. King, « A Vetustissimus Arabic Text on the Quadrans Vetus », dans Journal for the History of Astronomy, vol. 33, 2002, p. 237–255
- David A. King, « 14th-Century England or 9th-Century Baghdad? New Insights on the Elusive Astronomical Instrument Called Navicula de Venetiis », dans Centaurus, vol. 45, no 1-4, décembre 2003, p. 204–226
- David A. King, « Reflections on some new studies on applied science in Islamic societies (8th-19th centuries) », dans Islam & Science, 2004, June 2004
- David A. King, In Synchrony with the Heavens, Studies in Astronomical Timekeeping and Instrumentation in Medieval Islamic Civilization: Instruments of Mass Calculation, Brill Publishers, 2005 (ISBN 900414188X)
- « A Recently Discovered Sixteenth-Century Spanish Astrolabe », dans Ann. Sci., vol. 59, no 4, 2002, p. 331–362
- Alhazen (trad. Y. Tzvi Langermann), On the Configuration of the World, New York, Garland, coll. « Harvard Dissertations in the History of Science », 1990 (ISBN 0824000412)
- Michael E. Marmura, Review: An Introduction to Islamic Cosmological Doctrines. Conceptions of Nature and Methods Used for Its Study by the Ikhwan Al-Safa'an, Al-Biruni, and Ibn Sina by Seyyed Hossein Nasr, vol. 40, 1965, 744–746 p.
- O. S. Marshall, Alhazen and the Telescope, vol. 6, 1950
- Hossein Nasr, An Introduction to Islamic Cosmological Doctrines, State University of New York Press, 1993 (réimpr. 1993) (ISBN 0791415155)
- F. Jamil Ragep, « Tusi and Copernicus: The Earth's Motion in Context », dans Science in Context, Cambridge University Press, vol. 14, no 1-2, 2001a, p. 145–163
- F. Jamil Ragep, « Freeing Astronomy from Philosophy: An Aspect of Islamic Influence on Science », dans Osiris, 2nd Series, vol. 16, no Science in Theistic Contexts: Cognitive Dimensions, 2001b, p. 49–64 & 66–71
- F. Jamil Ragep, Teresi Dick et Roger Hart, Ancient Roots of Modern Science, Talk of the Nation (National Public Radio discussion; astronomy is discussed in the first fifteen-minute segment), 2002 [lire en ligne (page consultée le 22 janvier 2008)]
- Roshdi Rashed, The Celestial Kinematics of Ibn al-Haytham, vol. 17, Cambridge University Press, 2007, 7–55 p.
- Edward Rosen, The Dissolution of the Solid Celestial Spheres, vol. 46, 1985, 13–31 p.
- A. I. Sabra, « Configuring the Universe: Aporetic, Problem Solving, and Kinematic Modeling as Themes of Arabic Astronomy », dans Perspectives on Science, vol. 6, 1998, p. 288–330
- George Saliba, « The First Non-Ptolemaic Astronomy at the Maraghah School », dans Isis, vol. 70, no 4, 1979, p. 571–576
- George Saliba et Joseph Strayer (dir.), Al-Biruni, vol. 2 : Dictionary of the Middle Ages, New York, Charles Scribner's Sons, 1980
- George Saliba, « Review: Geschichte des arabischen Schriftiums. Band VI: Astronomie bis ca. 430 H by F. Sezgin », dans Journal of the American Oriental Society, vol. 101, no 2, 1981, p. 219–221
- George Saliba, « Early Arabic Critique of Ptolemaic Cosmology: A Ninth-Century Text on the Motion of the Celestial Spheres », dans Journal for the History of Astronomy, vol. 25, 1994a, p. 115–141
- George Saliba, A History of Arabic Astronomy: Planetary Theories During the Golden Age of Islam, New York University Press, 1994b (ISBN 0814780237)
- George Saliba, Whose Science is Arabic Science in Renaissance Europe?, Columbia University, 1999 [lire en ligne (page consultée le 2008-01-22)]
- George Saliba, « Arabic versus Greek Astronomy: A Debate over the Foundations of Science », dans Perspectives on Science, vol. 8, 2000, p. 328–341
- George Saliba, Lecture at SOAS, London - Part 3/7, Muslim Heritage & YouTube, 2007 [lire en ligne (page consultée le 2008-01-22)]
- C. Singer, A Short History of Scientific Ideas, Oxford University Press, 1959
- H. Suter, Mathematiker und Astronomen der Araber, 1902
- Seyyed Muhammad Husayn Tabatabaei, Tafsir al-Mizan
- G. M. Wickens et Roger M. Savory (dir.), Introduction to Islamic Civilization, The Middle East as a world Centre of science and medicine, Cambridge University Press, 1976, 111–118 p. (ISBN 052109948X)
- Salah Zaimeche, The Muslim Pioneers of Astronomy, Foundation for Science Technology and Civilisation, 2002 [lire en ligne (page consultée le 2008-01-22)]
Articles connexes
Liens externes
Catégories :- Histoire de l'astronomie
- Monde arabo-musulman
- Histoire des sciences dans le monde arabo-musulman
Wikimedia Foundation. 2010.