- Projection orthographique
-
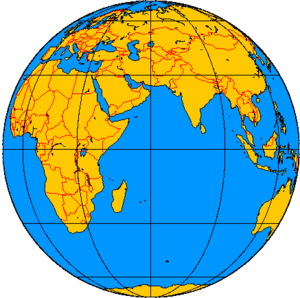projection orthographique équatoriale de l'hémisphère 30° ouest–150° est
Une projection orthographique est un type de projection cartographique. C'est, comme une projection stéréographique et une projection gnomonique, une projection de perspective par laquelle une sphère est projetée sur un plan tangent. Le point de perspective est à une distance infinie. On perçoit un hémisphère du globe comme si on était situé dans l'espace. Les surfaces et formes sont déformées, mais les distances sont préservées sur des lignes parallèles.
Sommaire
Histoire
Les anciens Grecs l'appelaient analemme, du nom d'un traité de Ptolémée. Le nom contemporain fut repris du De Architectura[1] de Vitruve par le mathématicien François d'Aguilon (1613). Albrecht Dürer grava pour illustrer le livre du cartographe Johannes Stabius les premières mappemondes polaires et équatoriales de la Terre en projection orthographique. Les photographies de la Terre et des autres planètes prises de l'espace ont donné un regain d'actualité à ce type de projection en astronomie.
Mathématiques
On obtient les formules de la projection orthographique, qui relient longitude λ et latitude Φ sur la sphère, aux coordonnées cartésiennes (x, y) dans le plan tangent par trigonométrie. Si l'on note R le rayon de la sphère et (λ0, Φ1) les coordonnées du centre de la projection (pris comme origine), ces formules sont :
![\begin{cases}
x = R\,\cos\phi\sin\left(\lambda - \lambda_0\right) \\
y = R\,\Big[\cos\phi_1\sin\phi - \sin\phi_1\cos\phi\cos\left(\lambda-\lambda_0\right)\Big]~.
\end{cases}](4/5f4cca0ede489a9bee827648d44b12af.png)
Il faut, bien sûr, éliminer les latitudes correspondant à des points en dehors de la carte, ce que l'on peut faire en calculant l'écart angulaire c au centre de la projection. De cette façon les points de l'hémisphère complémentaire ne seront pas tracés :
.
Dans cette formule, il ne faut pas représenter un point si cosc est négatif.
Inversement, pour retrouver les coordonnées (λ, Φ) d'un point sur la sphère, R, λ0, Φ1, x et y étant donnés :
où
Note
- De Architectura, livre I, chap. 4. Vitruve désigne par orthographie une vue géométrale d'un objet, qu'on appelle en géométrie descriptive l' élévation.
Références
- Snyder, J. P. - Flattening the Earth: two thousand years of map projections (1993), The University of Chicago Press, (ISBN 0-226-76747-7)
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Orthographic projection (cartography) » (voir la liste des auteurs)
Lien externe
(en) Eric W. Weisstein, « Orthographic Projection », MathWorld
Wikimedia Foundation. 2010.
