- Ptolemee
-
Ptolémée
 Pour les articles homonymes, voir Ptolémée (homonymie).
Pour les articles homonymes, voir Ptolémée (homonymie).Ptolémée 
Ptolémée d'après une gravure allemande du XVIe siècleNaissance Vers 90
Haute-Égypte (Province romaine de l’Égypte)Décès 168
Canope (Province romaine de l’Égypte)Champ(s) Astronomie, mathématiques, géographie, astrologie Célèbre pour Almageste Claudius Ptolemaeus (en grec : Κλαύδιος Πτολεμαῖος), communément appelé Ptolémée (Ptolémaïs de Thébaïde (Haute-Égypte) vers 90 - Canope vers 168) était un astronome et astrologue grec qui vécut à Alexandrie (Égypte). Il est également l’un des précurseurs de la géographie. Sa vie est mal connue. Son cognomen (surnom) Ptolémée semble indiquer des origines gréco-égyptiennes, et son nomen (nom) Claudius une citoyenneté romaine. Son praenomen (prénom) est inconnu.
Ptolémée fut l’auteur de plusieurs traités scientifiques, dont deux ont exercé par la suite une très grande influence sur les sciences islamique et européenne. L’un est le traité d’astronomie, qui est aujourd’hui connu sous le nom d’Almageste (arabisation de Ἡ Μεγάλη Σύνταξις, La Grande Composition puis Ὴ μεγίστη, La Très Grande, al-Mijisti, mais dont le titre original en grec était Μαθηματική σύνταξις, Composition mathématique). L’autre est la Géographie, qui est une discussion approfondie sur les connaissances géographiques du monde gréco-romain.
L’œuvre de Ptolémée est un sommet et l’aboutissement d’une longue évolution. Avec l’œuvre d’Aristote, c’est essentiellement à travers elle, transmise à la fois par les Arabes et les Byzantins, que l’Occident redécouvrira la science grecque au Moyen Age[N 1] et à la Renaissance[1], laissant leurs prédécesseurs dans l’obscurité[2]. Pourtant Ptolémée ne manque pas de faire abondamment référence à ceux-ci[N 2] dans ses écrits.
Sommaire
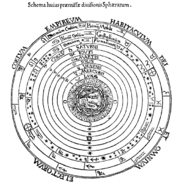
Astronomie
Article détaillé : Almageste.L’Almageste est le seul ouvrage complet sur l’astronomie de l’antiquité qui nous soit parvenu. Les astronomes babyloniens avaient mis au point des techniques de calcul pour la prévision de phénomènes astronomiques. Surtout, ils avaient consigné soigneusement, pendant des siècles, de précieuses observations (positions des astres, éclipses…)[N 3] Les astronomes grecs, tels qu’Eudoxe de Cnide et surtout Hipparque, avaient intégré ces observations et les leurs dans des modèles géométriques (théorie des épicycles) pour calculer les mouvements de certains corps célestes. Dans son traité, Ptolémée reprend ces différents modèles astronomiques et les perfectionne[3], notamment en ajoutant la notion d’équant[4]. Ses observations, jointes aux données antérieures dont il disposait, couvrent ainsi une période de près de neuf siècles. Ses « tables » de données, indispensables pour déterminer la position des astres, ont en effet comme point de départ le premier jour du calendrier égyptien de la première année du règne de Nabonassar, c’est-à-dire le 26 février 747 av. J. C.[5]. Ptolémée consacre donc le modèle géocentrique d’Hipparque, qui lui fut souvent attribué[N 4] et qui fut accepté pendant plus de mille trois cents ans, quoique de manière discontinue. En Europe occidentale, en effet, il sombra dans l’oubli au début du Moyen Age, avant d’être redécouvert à la fin de cette période. Cet héritage fut cependant préservé dans le monde arabe et, avec des hauts et des bas, dans l’Empire romain d’Orient et plus spécifiquement à Byzance[6]. Sa méthode et son modèle de calcul ont d’ailleurs été adoptés avec quelques modifications dans le monde arabophone et en Inde car ils étaient d’une précision suffisante pour satisfaire les besoins des astronomes, des astrologues, des détenteurs de calendriers et des navigateurs.
Ptolémée réalisa aussi une sorte de manuel essentiellement pratique, appelé « Les tables faciles » ou parfois « Les tables manuelles » (Πρόχειροι κανόνες), dérivé de l’Almageste[N 5] et destiné à réaliser des calculs de position des astres et d’éclipses.
Contrairement à une idée reçue, Ptolémée ne reprit pas à son compte l’idée d’Aristote selon laquelle les astres étaient placés sur des sphères de cristal[7]. Il dit même expressément que « les astres nagent dans un fluide parfait qui n’oppose aucune résistance à leurs mouvements[8]". On ignore si cette vision, proche de la notion de vide, était déjà présente chez Hipparque ou si elle doit être mise au crédit de Ptolémée. Pour celui-ci, déférents et épicycles sont donc immatériels. Nicolas Halma considère en outre que son choix du système des épicycles plutôt que de celui des excentriques résulte davantage d’une volonté de rendre les calculs plus commodes, que d’une foi dans la réalité matérielle du système[N 6].
Durant les treize siècles qui suivirent, l’astronomie ne progressa plus guère. L’Almageste et les tables faciles ne reçurent que des corrections mineures, bien qu’elles aient fait l’objet, à la fin de l’Antiquité, de nombreuses publications de la part des « commentateurs"[9], dont le plus connu est Théon d’Alexandrie. Ce furent donc les tables et les textes de Ptolémée qui furent utilisés directement ou indirectement comme références[10] jusqu’à ce que les progrès des instruments d’observation et la théorie élaborée par Nicolas Copernic et perfectionnée par Johannes Kepler n’entraînent son abandon. Mais ce fut à grand peine : le système héliocentrique de Copernic (1543), appuyé par Galilée fut rejeté par l’Église catholique et ce dernier fut condamné à abjurer en 1633.
L’Almageste contient également un catalogue de 1022 étoiles et une liste de quarante-huit constellations. Bien que ne couvrant pas toute la sphère céleste, ce système fut la référence pendant de nombreux siècles. Ptolémée a aussi décrit l’astrolabe, inventé probablement par Hipparque.
Géographie
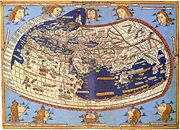
Article détaillé : Géographie (Ptolémée).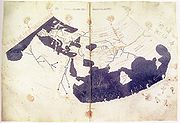 La carte du monde de Ptolémée, reconstituée au XVe siècle à partir de sa Géographie, indique les pays de Serica, Sinae (Chine) à l’extrême droite, au-delà de l’île de Taprobane (Sri Lanka, trop grande) et l’Aurea Chersonesus (Asie du Sud-Est)
La carte du monde de Ptolémée, reconstituée au XVe siècle à partir de sa Géographie, indique les pays de Serica, Sinae (Chine) à l’extrême droite, au-delà de l’île de Taprobane (Sri Lanka, trop grande) et l’Aurea Chersonesus (Asie du Sud-Est)
Sa Géographie est une autre œuvre majeure. Il s’agit d’une compilation des connaissances de la géographie du monde à l’époque de l’empire romain sous le règne d’Hadrien (125). Ptolémée s’est essentiellement appuyé sur les travaux d’un autre géographe, Marinus de Tyr[N 7], et sur les index géographiques des empires romain et perse, mais la plupart de ses sources au-delà du périmètre de l’empire étaient d’origines douteuses.
La première partie de la Géographie est une discussion sur les données et les méthodes qu’il a utilisées. Comme pour le modèle du système solaire dans l’Almageste, Ptolémée unifia dans un grand ensemble toutes les informations dont il disposait. Il attribua des coordonnées à tous les lieux et particularités géographiques qu’il connaissait, dans une grille qui couvrait le globe. La latitude était mesurée à partir de l’équateur, comme aujourd’hui, mais Ptolémée préférait l’exprimer selon la durée du jour le plus long plutôt qu’en degrés (la durée du solstice d’été passe de 12 h à 24 h au fur et à mesure qu’on s’éloigne de l’équateur vers le cercle polaire). Il fixa le méridien de longitude 0 au point le plus à l’ouest qu’il connaissait, les îles « Fortunata » (ou îles des Bienheureux), qui correspondent sans doute aux îles du Cap Vert, et non aux Canaries, comme on l’a souvent affirmé[N 8].
Ptolémée imaginait aussi et fournissait des méthodes pour dessiner des cartes, à la fois de tout le monde habité (écoumène) et des provinces romaines. Dans la deuxième partie de la Géographie, il fournissait les listes topographiques nécessaires, et des légendes aux cartes. Son écoumène couvrait 180 degrés de longitude des "îles des Bienheureux" (dans l’océan Atlantique) jusqu’à la Chine, et environ 80 degrés de latitude de l’Arctique aux Indes et loin en Afrique. Ptolémée était bien conscient que ses connaissances ne couvraient qu’un quart du globe.
Malheureusement, les plus vieilles cartes des manuscrits de la Géographie de Ptolémée ne datent que de 1300 environ, après la redécouverte du texte par le Byzantin Maximus Planudes.
Des cartes fondées sur des critères scientifiques ont été réalisées depuis l’époque d'Ératosthène, mais Ptolémée améliora les techniques de projection cartographique. Une carte du monde développée sur la base de sa Géographie fut exposée à Autun en France à la fin de l’époque romaine. À partir du XVe siècle, les premières reproductions sur papier imprimé firent leur apparition. Le premier exemplaire de la Géographie de Ptolémée fut édité avec les cartes à Bologne en 1477, rapidement suivi par une édition romaine de 1478.
Cet ouvrage fut jusqu’au XVIe siècle le guide de tous les voyageurs qui, à chaque découverte, croyaient reconnaître quelque contrée déjà indiquée par celui-ci. Ptolémée estimait la circonférence de la terre, à laquelle il donnait une forme sphérique, à 180 000 stades (environ 33 345 km). Pour la partie habitable, il assignait une longitude de 72 000 stades et une latitude de 40 000 stades[11].
Astrologie
Article détaillé : Tetrabiblos.Le traité de Ptolémée sur l’astrologie, le Tetrabiblos (tetra signifie en grec « quatre » et biblos « livre »), était l’ouvrage astrologique le plus célèbre de l’antiquité mais qui n’atteignait pas le statut de l’Almageste. Il exerça une grande influence dans l’étude des corps célestes dans la sphère sublunaire. Ainsi, il fournissait des explications des effets astrologiques des planètes, en fonction de leurs effets chauffant, rafraîchissant, mouillant, et séchant. Celui-ci traite en particulier de l’astrologie horoscopique en quatre livres qui consiste en une interprétation thématique à l’aide de l’érection d’une carte basée sur un tableau déterminant l’emplacement des sept planètes (Soleil compris) connues de l’époque à un moment donné.
Ptolémée estimait que l’astrologie est comme la médecine qui est hypothétique en raison de nombreux facteurs variables à prendre en compte. Ces facteurs étaient pour lui principalement, la race, le pays et l’éducation qui devaient affecter une personne au même titre que la position des planètes dans le ciel au moment de la naissance.
A la différence de Vettius Valens, il semble aujourd’hui que Ptolémée, surtout connu pour son traité sur l’astronomie, était un compilateur (un théoricien) en astrologie[12].
Musique
Ptolémée a également écrit les Harmoniques, un traité de musicologie de référence sur la théorie et les principes mathématiques de la musique[13]. Après une critique des approches de ses prédécesseurs, Ptolémée y plaide pour baser des intervalles musicaux sur des proportions mathématiques (contrairement aux partisans d’Aristoxène) soutenus par observation empirique (contrairement à l’approche purement théorique de l’École pythagoricienne). Il a présenté ses propres divisions du tétracorde et de l’octave, qu’il a dérivés avec l’aide d’un monocorde. L’intérêt de Ptolémée pour l’astronomie apparaît également dans une discussion sur la musique des sphères.
Les Harmoniques contribua très largement au développement de la théorie musicale au XVIe siècle.
Mathématiques
Article détaillé : Théorème de Ptolémée.Ptolémée a découvert un théorème qui dit que dans un quadrilatère convexe inscrit dans un cercle, le produit des diagonales est égal à la somme des produits des côtés opposés[14].
Dans sa Composition mathématique (Almageste), Ptolémée veut suivre la méthode rigoureuse de la géométrie et procéder par la démonstration introduite par les mathématiciens de la Grèce antique.
Autres travaux
- Dans l’Optique, Ptolémée traite des propriétés de la lumière notamment, la réflexion, la réfraction et la couleur. Ce travail est une partie importante de l’histoire de l’optique.
Notes et références
Notes
- ↑ Essentiellement au XIIe siècle, avec Gérard de Crémone pour les sources arabes.
- ↑ En particulier à Hipparque. Voir par exemple Almageste, IV, 2, où il souligne la qualité de ses observations de l’anomalie lunaire. Mais Gérard de Crémone dans sa traduction de l’Almageste ne reconnaît pas Hipparque sous son appellation arabe Abrachir.
- ↑ De nombreuses tablettes en cunéiformes avec ce type de contenu nous sont parvenues. Les plus anciennes dont nous disposons sont du VIIe siècle av. J.-C.
- ↑ On parle souvent du « système de Ptolémée ». Ce n’est pas faux, si l’on entend par là « le système utilisé par Ptolémée », mais l’expression donne à croire qu’il en est l’initiateur, ce qui est inexact. Ptolémée lui-même, dans l’Almageste, parle des épicycles d’Hipparque dans plusieurs passages relevés dans la préface de N. Halma.
- ↑ Certaines tables y sont cependant plus précises que dans l’Almageste, allant parfois jusqu’à la sixte d’angle (la tierce vaut 1/60 de seconde, la quarte 1/60 de tierce etc.). Ceci montre que Ptolémée, même après la publication de l’Almageste, n’a cessé d’affiner son travail. Les « Tables faciles » figurent également dans l’édition Halma, où elles sont considérées comme une sorte d’appendice à l’Almageste. Mais elles sont clairement postérieures.
- ↑ Voir sur ce point l’analyse très pointue de Halma, préface : "(Ptolémée) ne regardoit pas, lui-même, les siennes (ses hypothèses), comme réelles, mais seulement comme des moyens d’expliquer l’ordre céleste qu’il avoit paru impossible à Hipparque d’expliquer autrement que par cette complication de cercles. Nous pensons, dit-il dans son liv. III, qu’il convient de démontrer les phénomènes par les hypothèses les plus simples, pourvu que ce qu’elles supposent ne paroisse contredit en rien d’important par les observations (…) Elle se trouve confirmée par la manière dont Ptolémée énonce ces hypothèses et les déductions qu’il en tire. Il se sert presque toujours du futur ἔσαι sera, ou du conditionnel au lieu du temps présent, comme dans le ch. 4 du liv. IV, où il dit que les similitudes non seulement des rapports, mais encore des temps de l’un et de l’autre mouvement seroient ainsi sauvées (διασώζοιντο ἄν). Le choix arbitraire qu’il propose dans son liv. III, de l’excentrique ou de l’épicycle pour expliquer le mouvement du soleil, montre bien qu’il ne regardoit pas l’un comme plus réel que l’autre. Il a choisi dans les moyens que la géométrie lui fournissoit, ceux qu’il jugeoit les plus propres à représenter les effets dont il vouloit rendre compte, « La géométrie n’est qu’un instrument dans les mains de l’astronome », dit Bailly, cet instrument ne crée rien, mais en se prêtant à l’usage qu’on en fait sur de bonnes observations, il donne des résultats justes."
- ↑ Marinus intègre lui-même les apports d’Eratosthène et d’Hipparque. Voir Histoire de la géographie.
- ↑ Voir à ce sujet [1]. Cette interprétation est d’ailleurs visiblement celle qui est adoptée sur les cartes reproduites dans l’article.
Références
- ↑ Voir Renaissances médiévales.
- ↑ Sciences grecques- Moyen Âge - Figure de la Terre dans l’Antiquité - L. Génicot, Les lignes de faîte du Moyen Age, Casterman, 1961
- ↑ Ces faits sont indiqués, par petites touches, dans l’Almageste elle-même et soulignés dans la préface de l’édition Halma (Voir bibliographie).
- ↑ Voir géocentrisme.
- ↑ Astronomie babylonienne - J. Mogenet, A. Tihon, R. Royez, A. Berg, Nicéphore Grégoras : Calcul de l’éclipse de soleil du 16 Juillet 1330, Corpus des astronomes byzantins, I, Gleben, 1983, page 96 - Ptolémée, Almageste III, 6.
- ↑ Voir Sciences et techniques dans l'empire byzantin
- ↑ P. Couderc, Histoire de l’astronomie, Que sais-je n°165, pp.56 et ss.
- ↑ Almageste, XIII,12. - Halma, Op. cit., préface, pp. 15-16.
- ↑ A. Tihon, Théon d’Alexandrie et les « Tables Faciles » de Ptolémée, Archives internationales d’histoire des sciences, 1985 (35), n° 1124-115, p. 106-123. ISSN 0003-9810.
- ↑ Comme exemple de l’emploi tardif des textes de Ptolémée, on peut trouver les détails d’un calcul d’éclipse selon l’Almageste et selon les Tables faciles dans J. Mogenet, A. Tihon, R. Royez, A. Berg, Op. cit.
- ↑ Nouvelle biographie générale depuis les temps les plus reculés jusqu’à nos jours. De Hoefer (Jean Chrétien Ferdinand), tome 41, page 161 (Firmin Didot, Paris - 1866)
- ↑ Source: (en) A history of horoscopic astrology, par James Herschel Holden, American Federation of Astrologers, 2e édition, 1996)
- ↑ Études sur le Timée de Platon. Thomas Henri Martin, Plato. Tome I, page 412 (Ladrange, Paris - 1841)
- ↑ (fr) Ptolémée sur le site personnel de Serge Mehl
Bibliographie
Œuvres de Claude Ptolémée
- L’Almageste (vers 140), Éditée et traduite par l’abbé N. Halma, Paris, 2 vol., 1813-1817, puis réimprimée en 2 volumes (Hermann, Paris - 1927). « Transcrite » dans Ptolemy's Almagest, G. J. Toomer, Londres, 1984 (rééd. Princeton, 1998) et repris dans Le livre unique de l’astrologie (synthèse de l’œuvre de Ptolémée), éditions Nil, 2000, ISBN 2-84111-159-8. L’édition Halma est téléchargeable : [2]
- Les tables faciles, dans Halma (cf. supra).
- Les sentences : Claude Ptolémée, La tétrabible ou les quatre livres des jugements des astres, suivi de Le centiloque ou les cent sentences, traduction de Nicolas Bourdin. Paris, Culture, Art, Loisirs, 1974, 285 p.
- La Tétrabible, Loge Astrologique de France, 1985. La bible de l’astrologie antique (Jean-Baptiste Morin de Villefranche fera la bible de l’astrologie classique). Extraits : Manuel d’astrologie. La Tétrabible, introduction de Elizabeth Teissier, Les Belles Lettres, collection « Aux sources de la tradition », 1993.
- Traité de géographie. Claude Ptolémée (Ebherhart, Paris - 1828)
- Théorie harmonique, relevant de l’ouvrage originel Les Harmoniques. Texte en grec édité par Ingemar Düring, Die Harmonielehre des Klaudios Ptolemaios, Göteborg, Elander, 1930.
Études sur Claude Ptolémée
- Germaine Aujac, Claude Ptolémée, astronome, astrologue, géographe, Comité des travaux, 1995.
- Pierre Costabel, Ptolémée (Claude) IIe siècle après J.-C., dans Encyclopædia Universalis, Paris, av. 1989 ; mis à jour ap. 1993 [consulté dans l’éd. de 2004].
- Préface et notes de l’édition Halma (cf. supra).
Hommages
- L’astéroïde (4001) Ptolémée (4001 Ptolemaeus) a été nommé en son honneur, tout comme les cratères Ptolémée sur Mars et sur la Lune et aussi une tempête sur Vénus.
Voir aussi
Liens internes
- Almageste
- Figure de la Terre dans l’Antiquité
- Géocentrisme
- Histoire de l’astronomie
- Monde (univers)
- Révolution copernicienne
- Sciences grecques
Lien externe
- Portail de l’astronomie
- Portail de la géographie
- Portail de la Grèce antique
- Portail des mathématiques
Catégories : Personnalité du IIe siècle | Géographe | Astronome | Astronome de la Grèce antique | Astrologue
Wikimedia Foundation. 2010.