Miroir (optique)

La loi de la réflexion optique est un des fondements de l'optique géométrique : elle indique que le rayon réfléchi est dans le plan d'incidence (défini par le rayon incident et la normale à la surface au point de réflexion) et que l'angle de réflexion est égal à l'angle d'incidence (angles mesurés par rapport à la normale).

Miroir plan

Un miroir plan est, en optique, une surface plane parfaitement réfléchissante. Toutefois, un dioptre, même en présence de réfraction, entraîne un phénomène de réflexion partielle. C'est pourquoi, il est possible, à travers une vitre, de voir à la fois son propre reflet et ce qui se trouve derrière.

image donnée par un miroir plan

Les lois de la réflexion (dite spéculaire) sont les mêmes.
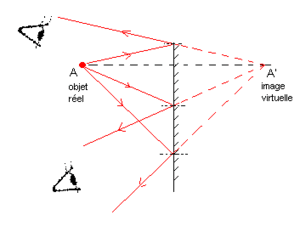
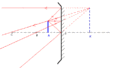
La conséquence est qu'un miroir est un système stigmatique rigoureux pour tout point et que l'image donnée par un miroir est une image virtuelle.

Dans la figure ci-contre, ont été représentés quelques rayons issus d'un objet lumineux réel et venant se réfléchir sur le miroir (que l'on schématise par un segment muni de hachure à l'arrière) selon les lois de Snell-Descartes.
Un observateur, et ce quelle que soit sa position, recevra de la lumière qui lui semble provenir d'un point symétrique de l'objet par rapport au miroir : l'image (virtuelle) que l'observateur voit.

Miroir courbe : généralités

Réflexion sur un miroir courbe convexe, plan tangent au point d'impact

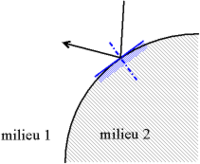
Dans le cas d'un miroir courbe, on considère localement le plan tangent à l'endroit de l'impact du rayon sur le miroir, et on applique la loi de la réflexion à ce plan tangent.

Le miroir est dit convexe si les rayons se réfléchissent à l'extérieur de la calotte (comme sur la figure ci-dessus), et concave si la réflexion se produit à l'intérieur de la calotte (comme sur la figure ci-dessous).

Notons que les miroirs courbes ne sont pas stigmatiques. En effet, les rayons partant d'un point ne se croisent pas tous au même point après avoir été réfléchis par le miroir, mise à part pour quelques points particulier (dans le cas du miroir sphérique, seuls le centre et les points du miroir donnent une « image unique »). Cependant, si l'on respecte les conditions de Gauss, c'est-à-dire :

• le rayon est presque parallèle à l'axe optique ;
• le rayon frappe le miroir à proximité de l'axe optique ;

alors, on peut considérer que le miroir est quasiment stigmatique.

Pour la distance, la notion de « proche » fait référence au rayon de courbure : la distance entre le sommet de la calotte située sur l'axe optique et le point d'impact du rayon est petit devant la courbure. Pour l'angle, dans le cas d'un miroir sphérique, cela signifie que l'angle α entre le rayon passant par le centre et la normale à l'impact du rayon vérifie : cos(α) est petit devant 1, ou plus précisément si ε désigne la distance entre le point émetteur A et le centre C, alors 2.(ε/r).cos(α)<<1.le principe du miroir et de réfléchir un objet pour donné une image.

Miroir sphérique

Un miroir sphérique est constitué d'une calotte sphérique, c'est-à-dire une sphère tronquée par un plan. L'ouverture du miroir est donc un cercle et l'axe du miroir est la droite normale à l'ouverture et passant par son centre.

• 

  Miroir sphérique convexe hors Gauss

• 

  Miroir sphérique concave hors Gauss

Le miroir sphérique n'est pas stigmatique. Il peut toutefois, si sa courbure est faible, être utilisé en stigmatisme approché. Il est alors représenté par un segment avec des hachures comme pour le miroir plan, mais avec l'indication de sa courbure par un trait "rabattu" aux extrémités.

Dans ce cas, des règles simples analogues à celles des lentilles minces permettent de déterminer par construction géométrique l'image d'un objet lumineux.

• 

  L'image est toujours plus petite

• 

  L'image est agrandie

• 

  L'image est plus petite et inversée

Autres miroirs courbes particuliers

Certains miroirs courbes sont fréquemment utilisés en raison de leurs propriétés particulières. Ce sont des miroirs dont la surface est obtenue en faisant tourner une conique (cercle, ellipse, parabole, hyperbole) autour de leur axe (la surface s'appelle respectivement une sphère, un ellipsoïde de révolution, un paraboloïde de révolution et un hyperboloïde de révolution). La notion mathématique de foyer de la conique (point permettant, avec la droite directrice et l'excentricité, de caractériser la conique) ne recoupe en général pas celle de foyer en optique géométrique (point où convergent les rayons venant de l'infini après déviation), sauf dans le cas de la parabole. Les courbes génératrices étant soit fermées, soit d'extension infinie, les miroirs réels sont donc des surfaces tronquées.

Miroir parabolique

Un miroir parabolique est un miroir dont la forme est une portion de paraboloïde de révolution. Ils furent notamment étudiés par le mathématicien italien Ghetaldi.

profil d'un miroir parabolique ; concentration au foyer

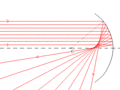
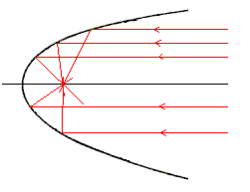
Les miroirs paraboliques concaves sont beaucoup utilisés soit pour produire des faisceaux de lumière parallèles, notamment dans des projecteurs, soit pour recueillir la lumière provenant d'une source lointaine et la concentrer en son foyer. Le principe est le même en vertu du principe du retour inverse de la lumière.

Ceci provient d'une propriété géométrique de la parabole : si l'on met une lampe au foyer de la parabole, les rayons réfléchis ressortent parallèles à l'axe de la parabole (le foyer géométrique est ici confondu avec le foyer optique).

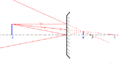
Dans le cas par exemple d'un projecteur à miroir parabolique, sans contre-miroir (figure de gauche ci-dessous), une partie du faisceau se perd et forme un halo diffus qui ne contribue pas au faisceau parallèle ; ce halo s'étend lorsque l'on s'éloigne du projecteur, et l'intensité de ce halo diminue. Avec un contre-miroir sphérique (figure de droite ci-dessous), tous les rayons sont récupérés, mais on a une tache sombre au centre. L'intensité récupérée par le contre-miroir est plus importante que l'intensité perdue dans la tache sombre ; par ailleurs, le faisceau n'étant pas parfaitement parallèle, la tache sombre s'estompe lorsque l'on s'éloigne du projecteur. Le réglage du contre-miroir est parfois délicat, son usage n'est donc pas systématique.

Projecteur à miroir parabolique : sans contre-miroir (figure de gauche), avec un contre-miroir sphérique (figure de droite)

La technique de miroir liquide permet d'obtenir des miroirs parfaitement paraboliques, et dont on peut régler la courbure.

Miroir elliptique

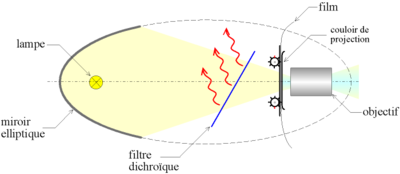
Un miroir elliptique épouse la forme d'un ellipsoïde de révolution. On utilise des miroirs elliptiques concaves pour former un faisceau lumineux convergent, par exemple dans les lanternes de projecteurs de cinéma.

Lanterne de cinéma

En effet, selon une propriété géométrique des ellipses, un rayon partant d'un foyer est réfléchi vers l'autre foyer (il s'agit là des foyers au sens géométrique, et non pas d'un point permettant la création d'un faisceau parallèle).

Ainsi, on place la lampe à un des foyers et le centre optique de l'objectif à l'autre foyer, ce qui permet de concentrer le flux de lumière.

Voir aussi

• Miroir dans le contexte commun
• Optique géométrique
• Stigmatisme
• Miroir plan
• Miroir sphérique

• Portail de la physique