Aryabhata

Statue d'Aryabhatta à l'IUCAA, Pune.

Âryabhata (आर्यभट) est le premier des grands astronomes de l'âge classique de l'Inde. Il naît en 476 à Ashmaka, mais passe l'essentiel de sa vie à Kusumapura que l'on identifie généralement comme Pataliputra, l'actuelle Patna, où il décède en 550. Il fut sans doute le plus grand mathématicien indien. Il est connu des Arabes sous le nom d'Aryabha et, en Europe médiévale, on l'appelle Ardubarius. Le premier satellite artificiel indien, lancé le 19 avril 1965, porte son nom.

Son livre, l'Âryabhatîya, est divisé en quatre parties :
(i) les constantes astronomiques et la table des sinus
(ii) les mathématiques nécessaires aux calculs
(iii) la division du temps et les règles pour calculer les longitudes des planètes en utilisant les excentriques et les épicycles
(iv) la sphère armillaire, les règles concernant les problèmes de trigonométrie et le calcul des éclipses.
Il y présente ses théories astronomiques et mathématiques dans lesquelles la Terre est considérée comme tournant autour de son axe et les distances des planètes sont exprimées par rapport à la distance Terre/Soleil, obéissant à un système héliocentrique. Âryabhata pense d'ailleurs que les planètes tournent autour du soleil suivant des orbites elliptiques. Il analyse la lumière émise par la Lune et les planètes comme celle du soleil réfléchie par ces astres. De même, il explique correctement les éclipses du Soleil et de la Lune, alors que la croyance indienne généralement suivie est que ces phénomènes sont causés par le démon Rahu. Dans le même livre, le jour est considéré d'un lever de soleil au suivant, tandis que dans son Âryabhata-siddhânta, il le compte d'un minuit au suivant. Il donne une durée de 365 jours 6 heures 12 minutes 30 secondes pour l'année, une valeur trop grande de quelques minutes.

Âryabhata écrit que 1582237500 rotations de la terre équivalent à 57753336 orbites lunaires.

Il s'agit d'une estimation très précise d'un rapport astronomique fondamental (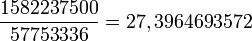) et c'est peut-être la constante astronomique la plus ancienne calculée avec une telle exactitude.

Âryabhata donne également une approximation précise de π. Dans l'Âryabhatîya, il écrit :

Ajoutez quatre à cent, multipliez ensuite le résultat par huit puis ajoutez alors soixante-deux mille. Le résultat est alors approximativement la circonférence d'un cercle d'un diamètre de vingt mille. Par cette règle, la relation de la circonférence au diamètre est donnée.

En d'autres termes, 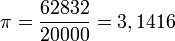. Comme 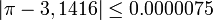il s'agit d'un résultat remarquable, exact à 10 ^{− 5} près.

Son œuvre, l'Âryabhatîya s'appelle aussi Ârya-Siddhânta (आर्य सिद्धान्त), « Siddhânta » étant un nom générique donné aux ouvrages scientifiques sanskrits.

Liens externes

• [pdf] Analyse du contenu mathématique de l'Âryabhatîya
• (en) Biographie, Université de St Andrew
• (en) Analyse du contenu astronomique de l'Âryabhatîya

• Portail du monde indien
• Portail de l’astronomie
• Portail des mathématiques