- Matrice diagonalisable
-
 Exemple de matrice diagonalisable sur le corps
Exemple de matrice diagonalisable sur le corps
des complexes mais pas sur celui des réels,
son polynôme caractéristique étant X2 + 1.En mathématiques, une matrice diagonalisable est une matrice carrée semblable à une matrice diagonale. Cette propriété est équivalente à l'existence d'une base de vecteurs propres, ce qui permet de définir de manière analogue un endomorphisme diagonalisable d'un espace vectoriel.
Le fait qu'une matrice soit diagonalisable dépend du corps dans lequel sont cherchées les valeurs propres, ce que confirme la caractérisation par le fait que le polynôme minimal soit scindé à racines simples.
Cette caractérisation permet notamment de montrer que les projecteurs sont toujours diagonalisables, ainsi que les involutions si le corps des coefficients est de caractéristique différente de 2. Plus généralement, les endomorphismes et matrices d'ordre fini sont diagonalisables sur le corps des complexes. Au contraire, un endomorphisme nilpotent non nul ne peut pas être diagonalisable.
Les matrices réelles symétriques sont diagonalisables par une matrice orthogonale. Plus généralement les matrices normales, parmi lesquelles les matrices hermitiennes, antihermitiennes et unitaires sont diagonalisables à l'aide d'une matrice unitaire, ce qui conduit au théorème spectral.
La diagonalisation est la détermination effective d'une matrice de passage transformant une matrice diagonalisable en une matrice diagonale, ou la décomposition d'un espace vectoriel en une somme directe de droites stables par un endomorphisme.
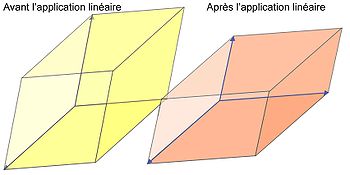 Fig. 1. Modification par un endomorphisme diagonalisable d'un parallélotope dont les côtés sont dirigés par des vecteurs propres.
Fig. 1. Modification par un endomorphisme diagonalisable d'un parallélotope dont les côtés sont dirigés par des vecteurs propres.
Sommaire
Définitions
Approche matricielle
Une matrice carrée M à coefficients dans un corps k est dite diagonalisable sur k s'il existe une matrice inversible P et une matrice diagonale D à coefficients dans k satisfaisant la relation :
Dans ce cas, chaque vecteur colonne Y de la matrice P est un vecteur propre pour la matrice M, c'est-à-dire qu'il existe un scalaire λ sur la diagonale de D tel que MY = λY.
Réciproquement, si une matrice admet une famille de vecteurs propres qui forment une base de l'espace des vecteurs colonnes alors cette matrice est diagonalisable. Il suffit de construire la matrice inversible formée par une juxtaposition de ces vecteurs, la matrice diagonale étant définie par la suite des valeurs propres associées.
Endomorphisme
Un endomorphisme d'un espace vectoriel est dit diagonalisable s'il existe une base de vecteurs propres. Cela signifie que l'espace vectoriel peut être décomposé en une somme directe de droites stables par l'endomorphisme, ou autrement dit que l'espace vectoriel est la somme directe des sous-espaces propres de l'endomorphisme[1].
En dimension finie, cette définition signifie que l'endomorphisme est représenté par une matrice diagonale dans cette base, donc que n'importe quelle représentation matricielle de l'endomorphisme est une matrice diagonalisable par changement de base.
Propriétés et critères
Par définition, toute matrice semblable à une matrice diagonalisable est également diagonalisable, ce qui peut se traduire pour les endomorphismes par le fait que le conjugué d'un endomorphisme diagonalisable par un automorphisme est également diagonalisable.
 Matrice de polynôme caractéristique X2
Matrice de polynôme caractéristique X2
mais dont le noyau est égal à l'image,
donc non diagonalisable.Plusieurs autres propriétés se déduisent directement de la forme diagonale :
- le noyau et l'image sont en somme directe ;
- le polynôme caractéristique est scindé : étant un invariant de similitude, il est le même pour une matrice diagonalisable M et pour une matrice diagonale D associée et s'écrit :

où (λi) décrit les coefficients diagonaux de D (une même valeur pouvant apparaitre plusieurs fois).
En revanche, une matrice dont le polynôme caractéristique est scindé n'est pas forcément diagonalisable, comme dans le cas des matrices nilpotentes non nulles.
Cependant, si le polynôme caractéristique est scindé à racines simples, chacune de ses racines est associée à une valeur propre et les vecteurs propres associés forment une base, montrant que la matrice est diagonalisable.
Puissances et polynômes
 Expression d'une puissance de matrice diagonale.
Expression d'une puissance de matrice diagonale.Les puissances d'une matrice diagonalisable s'expriment sous la forme
où la puissance de la diagonale se calcule en élevant simplement chaque coefficient diagonal à la même puissance k.
En conséquence, pour tout polynôme Q, la matrice Q(M) est égale à P.Q(D).P-1, et Q(D) s'exprime en appliquant simplement Q à chaque coefficient diagonal de D. On en déduit que Q(M) est nulle si et seulement si tous les coefficients diagonaux de D sont des racines du polynôme. Le polynôme minimal de M est donc le produit des facteurs (X-λ), où λ parcourt l'ensemble des coefficients diagonaux de D sans tenir compte de leur éventuelle multiplicité. En particulier, ce polynôme est scindé à racines simples.
Caractérisation
Par les polynômes
La réciproque de la dernière propriété énoncée ci-dessus peut se déduire de la décomposition de Dunford : si une matrice M annule un polynôme scindé, le polynôme minimal de M est scindé lui aussi. La matrice M est alors semblable à la somme d'une matrice diagonale D et d'une matrice nilpotente N dont l'indice de nilpotence est le plus petit commun multiple des ordres de multiplicité de chaque racine du polynôme minimal de M. Si de plus M annule un polynôme scindé à racines simples, alors son polynôme minimal est lui aussi scindé à racines simples, si bien que N est nilpotente d'ordre 1 c'est-à-dire nulle, et M est semblable à la matrice diagonale D.
Par les sous-espaces propres
Pour toute valeur propre λ d'une matrice M, on distingue :
- sa multiplicité géométrique, qui est la dimension du sous-espace propre associé, et
- sa multiplicité algébrique, qui est l'ordre de multiplicité de la racine λ dans le polynôme caractéristique de M (c'est aussi la dimension du sous-espace caractéristique associé).
La matrice M est diagonalisable si et seulement si la somme des multiplicités géométriques est égale à la taille de M. Or chaque multiplicité géométrique est toujours inférieure ou égale à la multiplicité algébrique correspondante. Par conséquent, une matrice est diagonalisable si et seulement si :
- son polynôme caractéristique est scindé et
- pour toute valeur propre, la multiplicité géométrique est égale à la multiplicité algébrique.
Racine
Le fait que toute puissance d'une matrice diagonalisable soit également diagonalisable admet une réciproque partielle. Toute matrice inversible admettant au moins une puissance non nulle diagonalisable est diagonalisable également sur un corps algébriquement clos de caractéristique nulle.
Ce résultat est une conséquence de la caractérisation ci-dessus par les polynômes. Soit A une matrice inversible dont une puissance An (avec n > 0) a pour polynôme minimal un polynôme scindé à racines simples s'écrivant :
Puisque A est inversible, sa puissance An l'est également donc toutes les racines de P sont non nulles. Il en découle que le polynôme suivant :
est également scindé à racines simples et est annulé par A, qui est donc diagonalisable.
 Exemple de matrice non diagonalisable modulo p
Exemple de matrice non diagonalisable modulo p
mais dont la puissance p-ième vaut l'identité modulo p.La condition d'inversibilité permet d'exclure les matrices nilpotentes dont une puissance est la matrice nulle qui est diagonalisable. La condition de clôture algébrique peut être affaiblie en supposant simplement que les valeurs propres de A admettent leurs racines d'ordre n dans le corps des coefficients. Enfin, il suffit que la caractéristique du corps soit première avec l'exposant de la puissance diagonalisable pour garantir que ces racines soient simples.
Dans une base orthonormale
Matrices symétriques
Toute matrice réelle symétrique est diagonalisable par une matrice orthogonale, c'est-à-dire que l'endomorphisme associé dans l'espace euclidien de dimension n est diagonalisable dans une base orthonormale. Réciproquement, si U est une matrice orthogonale et D une matrice diagonale réelle, alors le produit de matrices réelles UDU − 1 est une matrice symétrique.
Lorsqu'une matrice symétrique A est positive, c'est-à-dire si ses valeurs propres sont toutes positives, il existe une unique matrice symétrique positive dont le carré soit A. Cette racine carrée de A est en effet diagonalisable et a nécessairement les mêmes espaces propres avec des valeurs propres en racine carrée de celles de A.
Matrices normales
De même, toute matrice complexe hermitienne est diagonalisable par une matrice unitaire en une matrice diagonale réelle. Plus généralement, les matrices complexes diagonalisables par une matrice unitaire sont les matrices normales, c'est-à-dire qui commutent avec leur adjointe. Cette définition comprend à la fois les matrices hermitiennes, les antihermitiennes, les unitaires et en particulier leurs versions réelles : symétriques, antisymétriques et orthogonales. Cependant, ces deux dernières familles de matrice n'admettent pas en général de diagonalisation sur le corps des réels.
Application au théorème spectral
Le théorème spectral stipule qu'étant données deux formes bilinéaires symétriques sur un espace vectoriel réel ou complexe de dimension finie, si l'une d'entre elle est définie positive, il existe une base orthonormale pour celle-ci qui soit orthogonale pour l'autre.
Autrement dit, il existe une base dans laquelle les deux formes soient représentées par des matrices diagonales, la première étant même la matrice identité I. Si les deux formes ont respectivement pour matrice A et B dans une base arbitraire, et pour matrices I et B' dans la base particulière fournie par le théorème, les nouvelles matrices ne sont pas semblables aux anciennes, mais congruentes, via la matrice de passage P (inversible) et sa matrice adjointe P* :
 .
.
Pour démontrer le théorème il suffit de considérer, sur l'espace euclidien ou hermitien défini par la première forme, l'endomorphisme autoadjoint canoniquement associé à la seconde : il existe une base orthonormée (par rapport à la première forme) qui est propre pour cet endomorphisme (donc qui est orthogonale pour la seconde forme).
Répartition
La répartition des matrices diagonalisables dans l'ensemble des matrices carrées d'une taille donnée peut être estimée en termes de topologie, pour démontrer certains résultats par densité, ou en termes de mesure pour évaluer la probabilité qu'une matrice prise au hasard soit diagonalisable.
L'ensemble des matrices à coefficients réels ou complexes (d'une taille fixée) est muni d'une unique topologie séparée compatible avec sa structure d'espace vectoriel. Elle peut être obtenue par exemple à l'aide d'une norme matricielle. Le choix d'une base de l'espace des matrices permet en outre de définir une mesure de Lebesgue associée.
Sur le corps des complexes
Une partie des matrices diagonalisables est constituée de celles dont le polynôme caractéristique est à racines simples, c'est-à-dire de discriminant non nul. Comme ce discriminant est polynomial en les coefficients des matrices, son lieu d'annulation est un fermé. Par passage au complémentaire, les matrices dont le polynôme caractéristique est à racines simples forment donc un ouvert.
N'importe quelle matrice peut être approchée par de telles matrices en perturbant les coefficients diagonaux d'une matrice triangulaire semblable. L'ensemble des matrices diagonalisables contient donc un ouvert dense. Par passage au complémentaire, l'ensemble des matrices non diagonalisables (inclus dans le lieu d'annulation du discriminant) est donc rare, c'est-à-dire que son adhérence est d'intérieur vide.
Plus précisément, le lieu d'annulation du discriminant est une sous-variété algébrique (stricte) donc elle est de mesure nulle pour la mesure de Lebesgue (quelle que soit la base choisie) ou pour n'importe quelle mesure qui lui est absolument continue.
Enfin, l'ensemble des matrices diagonalisables est un cône, c'est-à-dire qu'il est stable par multiplication scalaire, donc il est connexe par arcs via la matrice nulle. En particulier, il est donc connexe.
Il est possible de démontrer aussi que l'ensemble des matrices diagonalisables inversibles est également connexe par arcs comme image du produit des matrices diagonales inversibles (isomorphe à un produit fini de copies du groupe des complexes non nuls) et du groupe linéaire, tous deux connexes par arcs.
Sur le corps des réels
Matrice carrée de taille 2, polynôme caractéristique et discriminant dont l'ensemble d'annulation
est le double cône représenté par projection sur l'ensemble des matrices de trace nulle.
Ce cône est la frontière de l'ensemble des matrices non diagonalisables (au-dessus et en-dessous),
séparé en deux composantes connexes par l'ensemble des matrices scalaires (sommet à l'origine).À partir de la dimension 2, l'ensemble des matrices diagonalisables sur le corps des réels n'est pas dense comme dans le cas complexe, donc l'ensemble des matrices non diagonalisables n'est pas négligeable pour la mesure de Lebesgue. En effet, l'ensemble des matrices réelles non diagonalisables sur les réels et dont le polynôme caractéristique est à racines simples sur le corps des complexes forme alors un ouvert non vide.
En dimension 2 ou 3, la diagonalisabilité d'une matrice est déterminée par le signe du discriminant de son polynôme caractéristique lorsqu'il est non nul. Le lieu d'annulation de ce discriminant réunit alors les matrices non diagonalisables même sur le corps des complexes et les matrices diagonalisables dont le polynôme caractéristique est à racines multiples.
Matrices simultanément diagonalisables
Plusieurs matrices sont dites simultanément diagonalisables si elles sont semblables à des matrices diagonales dans une même base.
Une condition nécessaire et suffisante pour un ensemble de matrices diagonalisables est que toutes les matrices de l'ensemble commutent deux à deux.
Une application de ce résultat concerne les représentations de groupes finis par des groupes de matrices complexes inversibles. Comme chaque élément du groupe est d'ordre fini, il annule un polynôme de la forme Xn − 1 qui est scindé à racines simples sur le corps des complexes. Donc chaque matrice de la représentation est diagonalisable. Si en outre le groupe est abélien, il existe une base dans laquelle toutes les matrices de la représentation sont diagonales.
Application à l'exponentielle matricielle
Les techniques de diagonalisation dépassent largement le cas de l'algèbre. L'exemple donné ici traite d'un cas d'analyse fonctionnelle. Comme souvent, dans ce contexte, des considérations topologiques supplémentaires sont nécessaires.
Il existe un cas particulier important d'équations différentielles, celui où elles sont linéaires. L'article sur les équations différentielles linéaires nous montre que sa résolution est intimement liée à la résolution de l'équation suivante, où a désigne un endomorphisme :

La fonction exponentielle sur l'espace des endomorphismes est l'unique solution de cette équation. Or, en dimension finie, sur le corps des nombres réels ou complexes, une analyse à l'aide d'une diagonalisation montre que cette fonction s'exprime sous la forme de la série d'endomorphismes suivante :

Cette fonction vérifie de plus la propriété suivante :
Si ab = ba alors exp(a + b) = exp(a)exp(b)
Pour le calcul effectif de la solution, une analyse plus poussée de la réduction des endomorphismes est nécessaire.
La démonstration donnée ici n'est pas la plus générale. Des résultats analogues se démontrent sur les algèbres de Banach.
DémonstrationsIl existe une unique fonction exp de la variable réelle ou complexe dans l'espace des endomorphismes de dimension finie sur le corps des réels ou des complexes, vérifiant l'équation suivante :

Cette fonction est définie par :

Démonstration. L'existence et l'unicité sont garanties par le théorème de Cauchy-Lipschitz. La convergence de la série est garantie par son absolue convergence. La démonstration suivante utilise celle de la borne du sup sur la boule unité. Il est à remarquer que la convergence ne suppose pas la dimension finie dans le cas où l'endomorphisme est continu.
Cas où a est diagonalisable. Soit (ei) une base de vecteurs propres, de valeurs propres (λi). Considérons alors l'endomorphisme exp . Il vérifie pour tout élément de la base :

L'équation (1) est donc vérifiée sur une base de l'espace vectoriel pour la fonction exp . Cette équation est linéaire et est donc vérifiée partout.
Cas complexe où a est quelconque. Utilisons alors un argument topologique ; remarquons que l'ensemble des endomorphismes diagonalisables est dense dans l'espace des endomorphismes. Il est donc possible de considérer une suite (ai) d'endomorphismes diagonaux convergeant vers a. Considérons alors la suite de fonctions
 , la suite des dérivées converge uniformément sur toute boule de centre a autour d'une valeur de t donnée. Cette même suite converge simplement. Par passage à la limite, l'égalité (1) est donc vérifiée pour a avec la fonction exponentielle.
, la suite des dérivées converge uniformément sur toute boule de centre a autour d'une valeur de t donnée. Cette même suite converge simplement. Par passage à la limite, l'égalité (1) est donc vérifiée pour a avec la fonction exponentielle.Cas réel. Il suffit de prolonger l'espace vectoriel en un espace vectoriel complexe, l'égalité (1) est alors vérifiée. Sa réduction au cas réel est donc aussi vérifiée.
Si ab = ba alors exp(a + b) = exp(a)exp(b).
Démontrons dans un premier temps que les endomorphismes b et exp(a) commutent. Soit
 un réel strictement positif. La série définissant l'exponentielle est absolument convergente, donc il existe un entier p tel que :
un réel strictement positif. La série définissant l'exponentielle est absolument convergente, donc il existe un entier p tel que :
Cette majoration démontre les deux inégalités suivantes :


De plus, b commutent avec a donc aussi avec toutes les puissances de a. Ce qui montre, en additionnant les deux majorations précédentes que :

La dernière inégalité démontre la commutativité cherchée.
Recherchons alors une solution à l'équation différentielle suivante :

Les deux calculs suivants :


montrent deux écritures de l'unique solution à l'équation différentielle. L'unicité de la solution prouve alors l'égalité. En particulier si t = 1 on obtient :

La dernière démonstration ne suppose pas la dimension finie, mais la continuité de a et de b.
Notes et références
- L'axiome du choix peut être nécessaire en dimension infinie pour justifier l'existence d'une base de chaque sous-espace propre et même pour exhiber une famille de vecteurs non nuls à partir d'une décomposition en droites vectorielles.
Voir aussi
Wikimedia Foundation. 2010.