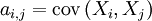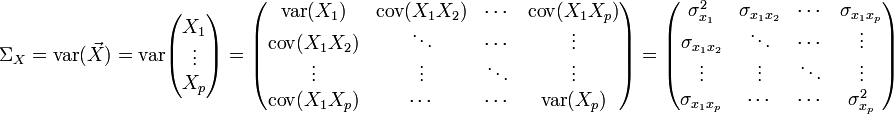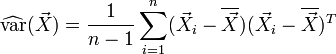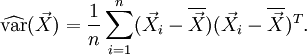Matrice De Variance-Covariance

Matrice De Variance-Covariance

Matrice de variance-covariance

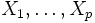Une matrice de variance-covariance est une matrice carrée caractérisant les interactions (linéaires) entre p variables aléatoires X_1,\dots,X_p\,.

Sommaire

Définition

La matrice de variance-covariance (ou simplement matrice de variance) d'un vecteur de p variables aléatoires 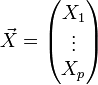\vec X=\begin{pmatrix} X_1 \\ \vdots\\ X_p \end{pmatrix} est la matrice carrée dont le terme générique est donné par:

a_{i,j}=\textrm{cov}\left(X_i,X_j\right)


La matrice de variance-covariance, notée parfois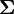 \boldsymbol\Sigma, est définie donc comme:

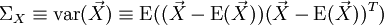
Définition — \Sigma_X\equiv\operatorname{var}(\vec X) \equiv \operatorname{E}((\vec X-\operatorname{E}(\vec X))(\vec X-\operatorname{E}(\vec X))^T)

En développant les termes:

\Sigma_X=\operatorname{var}(\vec X) = \operatorname{var}\begin{pmatrix} X_1 \\ \vdots\\ X_p \end{pmatrix} = \begin{pmatrix} \operatorname{var}(X_1) & \operatorname{cov}(X_{1}X_{2}) & \cdots & \operatorname{cov}(X_{1}X_{p}) \\ \operatorname{cov}(X_{1}X_{2}) & \ddots & \cdots & \vdots\\ \vdots & \vdots & \ddots & \vdots\\ \operatorname{cov}(X_{1}X_{p}) & \cdots & \cdots& \operatorname{var}(X_p) \end{pmatrix} = \begin{pmatrix} \sigma^2_{x_1} & \sigma_{x_{1}x_{2}} & \cdots & \sigma_{x_{1}x_{p}} \\ \sigma_{x_{1}x_{2}} & \ddots & \cdots & \vdots\\ \vdots & \vdots & \ddots & \vdots\\ \sigma_{x_{1}x_{p}} & \cdots & \cdots& \sigma^2_{x_p} \end{pmatrix}



Propriétés

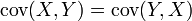  • La matrice est symétrique, étant donné la propriété que \operatorname{cov}(X, Y) = \operatorname{cov}(Y, X), .
  • Ses valeurs propres sont positives ou nulles. Lorsqu'il n'existe aucune relation affine presque sûre entre les composantes du vecteur aléatoire, la matrice 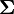\boldsymbol{\Sigma} est à valeurs propres strictement positives : elle est définie positive.
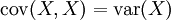
  • Les éléments de sa diagonale représentent la variance de chaque variable, étant donné la propriété que: \operatorname{cov}(X, X) = \operatorname{var}(X)
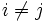  • Les éléments en dehors de la diagonale représentent la covariance entre les variables i et j quand \quad i \neq j.

Estimation

Un estimateur non-biaisé de la matrice de variance-covariance peut être obtenu par:

\operatorname{\widehat {var}}(\vec X)= {1 \over {n-1}}\sum_{i=1}^n (\vec X_i-\overline{\vec{X}})(\vec X_i-\overline{\vec{X}})^T
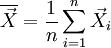où \overline{\vec X}={1 \over {n}}\sum_{i=1}^n \vec X_i est le vecteur des moyennes empiriques.

L'estimateur du maximum de vraisemblance, sous l'hypothèse que X suit une loi normale multidimensionnelle, vaut par contre:

\operatorname{\widehat {var}}(\vec X)={1 \over n}\sum_{i=1}^n (\vec X_i-\overline{\vec X})(\vec X_i-\overline{\vec X})^T.

Dans le cas où les données sont générées par une loi normale multidimensionnelle, l'estimateur du maximum de vraisemblance suit une loi de Wishart (en)

Utilisation en statistique

La matrice de variance-covariance est un outil essentiel pour l'analyse multivariée:

Test sur la matrice de variance-covariance

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Le test de sphéricité de Bartlett permet de déterminer si les composantes hors de la diagonale de la matrice sont différentes de zéro, i.e. si il y a une relation entre les différentes variables prises en considération.

Voir aussi

  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
Ce document provient de « Matrice de variance-covariance ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice De Variance-Covariance de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Matrice de variance-covariance — Une matrice de variance covariance est une matrice carrée caractérisant les interactions (linéaires) entre p variables aléatoires . Sommaire 1 Définition 2 Propriétés 3 …   Wikipédia en Français

  • Matrice de covariance — Matrice de variance covariance Une matrice de variance covariance est une matrice carrée caractérisant les interactions (linéaires) entre p variables aléatoires . Sommaire 1 Définition 2 Propriétés …   Wikipédia en Français

  • Variance (statistiques) — Variance (statistiques et probabilités) Pour les articles homonymes, voir Variance. En statistique et probabilité, la variance est une mesure arbitraire servant à caractériser la dispersion d une distribution ou d un échantillon. Sommaire 1… …   Wikipédia en Français

  • Variance (statistiques et probabilites) — Variance (statistiques et probabilités) Pour les articles homonymes, voir Variance. En statistique et probabilité, la variance est une mesure arbitraire servant à caractériser la dispersion d une distribution ou d un échantillon. Sommaire 1… …   Wikipédia en Français

  • Covariance — Pour le principe physique, voir Principe de covariance générale.  Ne pas confondre avec la covariance d un tenseur en algèbre ou en géométrie différentielle, ou d un foncteur en théorie des catégories. En théorie des probabilités et en… …   Wikipédia en Français

  • Variance (statistiques et probabilités) — Pour les articles homonymes, voir Variance. En statistique et probabilité, la variance est une mesure arbitraire servant à caractériser la dispersion d une distribution ou d un échantillon. Sommaire 1 Définition …   Wikipédia en Français

  • Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”