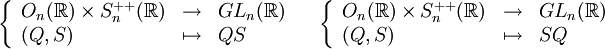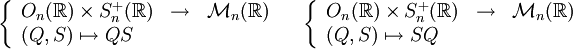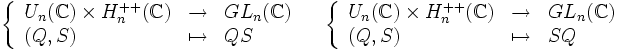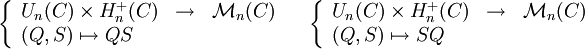Decomposition polaire

Decomposition polaire

Décomposition polaire

Sommaire

Décomposition polaire d'une matrice réelle

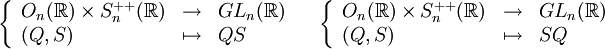
\left\{\begin{array}{lll} O_n(\R)\times S_n^{++}(\R) &\to &GL_n(\R)\\ (Q,S) &\mapsto & QS \end{array}\right.\quad \left\{\begin{array}{lll} O_n(\R)\times S_n^{++}(\R) &\to &GL_n(\R)\\ (Q,S) &\mapsto & SQ \end{array}\right.

Autrement dit, toute matrice inversible réelle se décompose de façon unique en produit d'une matrice orthogonale et d'une matrice symétrique strictement positive.

  • Les applications suivantes sont surjectives mais en général non injectives :
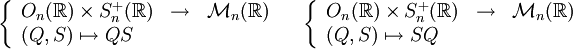
\left\{\begin{array}{lll} O_n(\R)\times S_n^{+}(\R) &\to &\mathcal M_n(\R)\\ (Q,S) \mapsto QS \end{array}\right.\quad \left\{\begin{array}{lll} O_n(\R)\times S_n^{+}(\R) &\to &\mathcal M_n(\R)\\ (Q,S) \mapsto SQ \end{array}\right.

Décomposition polaire d'une matrice complexe

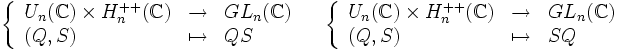
\left\{\begin{array}{lll} U_n(\mathbb C)\times H_n^{++}(\mathbb C) &\to &GL_n(\mathbb C)\\ (Q,S) &\mapsto & QS \end{array}\right.\quad \left\{\begin{array}{lll} U_n(\mathbb C)\times H_n^{++}(\mathbb C) &\to &GL_n(\mathbb C)\\ (Q,S) &\mapsto & SQ \end{array}\right.

Autrement dit, toute matrice inversible complexe se décompose de façon unique en produit d'une matrice unitaire et d'une matrice hermitienne strictement positive.

  • Les applications suivantes sont surjectives mais en général non injectives :
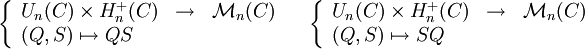
\left\{\begin{array}{lll} U_n(C)\times H_n^{+}(C) &\to &\mathcal M_n(C)\\ (Q,S) \mapsto QS \end{array}\right.\quad \left\{\begin{array}{lll} U_n(C)\times H_n^{+}(C) &\to &\mathcal M_n(C)\\ (Q,S) \mapsto SQ \end{array}\right.

Remarque. Pour n=1, on retrouve l'écriture z = reiθ d'un nombre complexe non nul. C'est la raison du nom de décomposition polaire : c'est une sorte de généralisation des coordonnées polaires.

Références

R. Mneimné, F. Testard, Introduction à la théorie des groupes de Lie classiques, Hermann 1986, (ISBN 2-70566-040-2) (voir pages 18–20)

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « D%C3%A9composition polaire ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Decomposition polaire de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Décomposition Polaire — Sommaire 1 Décomposition polaire d une matrice réelle 2 Décomposition polaire d une matrice complexe 3 Références 4 Voir aussi …   Wikipédia en Français

  • Décomposition polaire — Sommaire 1 Décomposition polaire d une matrice réelle 2 Décomposition polaire d une matrice complexe 3 Application 4 Références …   Wikipédia en Français

  • Decomposition en valeurs singulieres — Décomposition en valeurs singulières En mathématiques, le procédé d algèbre linéaire de décomposition en valeurs singulières (ou SVD, de l anglais : Singular Value Decomposition) d une matrice est un outil important de factorisation des… …   Wikipédia en Français

  • Décomposition En Valeurs Singulières — En mathématiques, le procédé d algèbre linéaire de décomposition en valeurs singulières (ou SVD, de l anglais : Singular Value Decomposition) d une matrice est un outil important de factorisation des matrices rectangulaires réelles ou… …   Wikipédia en Français

  • Décomposition en valeurs singulières — En mathématiques, le procédé d algèbre linéaire de décomposition en valeurs singulières (ou SVD, de l anglais : Singular Value Decomposition) d une matrice est un outil important de factorisation des matrices rectangulaires réelles ou… …   Wikipédia en Français

  • Décomposition de Cartan — En mathématiques, la décomposition de Cartan d un groupe de Lie ou d une algèbre de Lie semi simple joue un rôle important dans l étude de leur structure et de leurs représentations. Elle généralise la décomposition polaire du groupe linéaire.… …   Wikipédia en Français

  • Decomposition LU — Décomposition LU En algèbre linéaire, la décomposition LU est une méthode de décomposition d une matrice en une matrice triangulaire inférieure L (comme Low , bas) et une matrice triangulaire supérieure U (comme Up , haut). Cette décomposition… …   Wikipédia en Français

  • Décomposition lu — En algèbre linéaire, la décomposition LU est une méthode de décomposition d une matrice en une matrice triangulaire inférieure L (comme Low , bas) et une matrice triangulaire supérieure U (comme Up , haut). Cette décomposition est utilisée en… …   Wikipédia en Français

  • Decomposition QR — Décomposition QR En algèbre linéaire, la décomposition QR (appelée aussi, décomposition QU) d une matrice A est une décomposition de la forme A = QR où Q est une matrice orthogonale (QQT = I), et R une matrice triangulaire supérieure. Il existe… …   Wikipédia en Français

  • Décomposition QR — En algèbre linéaire, la décomposition QR (appelée aussi, décomposition QU) d une matrice A est une décomposition de la forme A = QR où Q est une matrice orthogonale (QQT = I), et R une matrice triangulaire supérieure. Ce type de décomposition est …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”