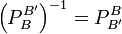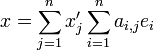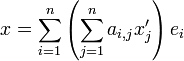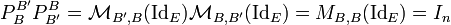Matrice De Passage
- Matrice De Passage
-
Matrice de passage
Une matrice de passage (ou encore matrice de changement de base) permet d'écrire des formules de changement de base pour les représentations matricielles des vecteurs, des endomorphismes, des formes bilinéaires.
Définition
Soient  un corps commutatif, E un K-espace vectoriel.
un corps commutatif, E un K-espace vectoriel.
Soient deux bases 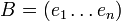 et
et 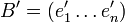 de E. Pour des raisons mnémotechniques on qualifie B' de nouvelle base, B d'ancienne base.
de E. Pour des raisons mnémotechniques on qualifie B' de nouvelle base, B d'ancienne base.
On définit ainsi la matrice de passage de B à B', notée 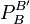 :
:
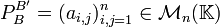 telle que
telle que ![\forall j \in [\![1,n]\!], \quad e'_j=\sum_{i=1}^n a_{i,j}e_i](/pictures/frwiki/50/27d81ad5b0f39251d7f260f525f7cb28.png)
Les colonnes de cette matrice ne sont autres que les vecteurs de la nouvelle base, exprimés dans l'ancienne base.
On peut aussi interpréter la matrice de passage comme la matrice représentative de l'application identité, de E muni de la base B' dans E muni de la base B. On a 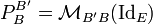 où
où 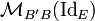 est la matrice de IdE relativement à B' et B.
est la matrice de IdE relativement à B' et B.
Théorème
Énoncé
Soit un vecteur 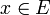 , ayant respectivement pour composantes
, ayant respectivement pour composantes 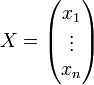 et
et 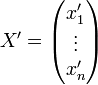 dans deux bases B et B'.
dans deux bases B et B'.
Alors 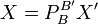
Démonstration
La décomposition du vecteur dans les deux bases nous donne 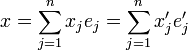
De plus, ![\forall j \in [\![1,n]\!], e'_j=\sum_{i=1}^n a_{i,j}e_i](/pictures/frwiki/52/4985b15a157beedf4bb7e5bc1ae62b70.png)
Par substitution,
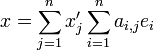
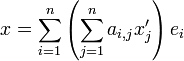
La décomposition du vecteur étant unique dans chaque base, on peut procéder à l'identification des coefficients :
![\forall i \in [\![1,n]\!], x_i=\sum_{j=1}^n a_{i,j} x'_j = \left(P_B^{B'}\cdot X'\right)_i](/pictures/frwiki/99/c758f44c1873c9f52be5143d291768ed.png) , d'où
, d'où 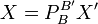
Inversibilité
Soient B et B' deux bases de E Alors 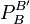 est inversible et
est inversible et 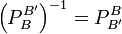
Démonstration
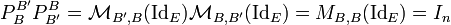
Voir aussi
|
Articles en rapport avec les matrices |
| Par forme |
|
| Transformée |
|
| En relation |
|
| Par propriété |
|
| Par famille |
|
| Particulière |
|
| Associée |
|
| Résultats |
|
| Voir aussi |
|
 Portail des mathématiques
Portail des mathématiques
Catégorie : Matrice remarquable
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Matrice De Passage de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Matrice de passage — Une matrice de passage (ou encore matrice de changement de base) permet d écrire des formules de changement de base pour les représentations matricielles des vecteurs, des applications linéaires et des formes bilinéaires. Sommaire 1 Définition 2… … Wikipédia en Français
Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice Circulante — En algèbre linéaire, une matrice circulante est une matrice carrée dans laquelle on passe d une ligne à la suivante par permutation circulaire (décalage vers la droite) des coefficients. Une matrice circulante de taille n est donc de la forme où… … Wikipédia en Français
Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D … Wikipédia en Français
Matrice Définie Positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou complexes : aT désigne la… … Wikipédia en Français
Matrice definie positive — Matrice définie positive En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou… … Wikipédia en Français
Matrice equivalente — Matrice équivalente En mathématiques, deux matrices de même taille (m,n), A et B sont dites équivalentes si et seulement s il existe deux matrices inversibles P et Q (respectivement de tailles (n,n) et (m,m)) telles que A = QBP − 1 Il s agit d… … Wikipédia en Français
Matrice Équivalente — En mathématiques, deux matrices de même taille (m,n), A et B sont dites équivalentes si et seulement s il existe deux matrices inversibles P et Q (respectivement de tailles (n,n) et (m,m)) telles que A = QBP − 1 Il s agit d une relation d… … Wikipédia en Français
 un corps commutatif, E un K-espace vectoriel.
un corps commutatif, E un K-espace vectoriel.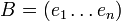 et
et 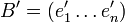 de E. Pour des raisons mnémotechniques on qualifie B' de nouvelle base, B d'ancienne base.
de E. Pour des raisons mnémotechniques on qualifie B' de nouvelle base, B d'ancienne base.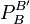 :
: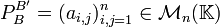 telle que
telle que ![\forall j \in [\![1,n]\!], \quad e'_j=\sum_{i=1}^n a_{i,j}e_i](/pictures/frwiki/50/27d81ad5b0f39251d7f260f525f7cb28.png)
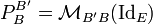 où
où 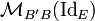 est la matrice de IdE relativement à B' et B.
est la matrice de IdE relativement à B' et B.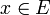 , ayant respectivement pour composantes
, ayant respectivement pour composantes 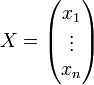 et
et 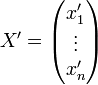 dans deux bases B et B'.
dans deux bases B et B'.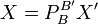
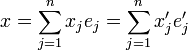
![\forall j \in [\![1,n]\!], e'_j=\sum_{i=1}^n a_{i,j}e_i](/pictures/frwiki/52/4985b15a157beedf4bb7e5bc1ae62b70.png)
![\forall i \in [\![1,n]\!], x_i=\sum_{j=1}^n a_{i,j} x'_j = \left(P_B^{B'}\cdot X'\right)_i](/pictures/frwiki/99/c758f44c1873c9f52be5143d291768ed.png) , d'où
, d'où 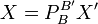
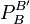 est inversible et
est inversible et