Fonction exponentielle

Fonction exponentielle
Page d'aide sur l'homonymie Pour les articles homonymes, voir Exponentielle.
Courbe représentative de la fonction x \mapsto \mathrm e^x

En mathématiques, la fonction exponentielle est la fonction notée exp qui est sa propre dérivée et qui prend la valeur 1 en 0. Elle est utilisée pour modéliser des phénomènes dans lesquels une différence constante sur la variable conduit à un rapport constant sur les images.

On note e la valeur de cette fonction en 1. Ce nombre e qui vaut approximativement 2,71828 s'appelle la base de la fonction exponentielle et permet une autre notation de la fonction exponentielle

\exp(x) = \mathrm e^x.~

La fonction exponentielle est la seule fonction continue sur ℝ qui transforme une somme en produit et qui prend la valeur e en 1. C'est un cas particulier des fonctions de ce type appelées exponentielles de base a

On peut la déterminer comme limite de suite ou à l'aide d'une série entière.

C'est la bijection réciproque de la fonction logarithme népérien.

Ces diverses définitions permettent d'étendre la définition de la fonction exponentielle à des fonctions de ℂ vers ℂ* ou même à des espaces plus compliqués et s'utilise alors en géométrie riemannienne, dans la théorie des groupes de Lie, ou encore dans l'étude des algèbres de Banach.

Les applications élémentaires des fonctions exponentielles réelles ou complexes concernent la résolution des équations différentielles, la mise en place de la théorie de Fourier… mais les champs d'applications des fonctions exponentielles sont extrêmement vastes : étude de la croissance des groupes, etc.

On appelle aussi parfois fonction exponentielle toute fonction dont l'expression est de la forme f(x)=A\mathrm e^{\lambda x} \,.

Sommaire

Fonction exponentielle réelle

Définitions

Il existe plusieurs points d'entrée possible pour la définition de la fonction exponentielle : par la propriété de sa dérivée (dérivée égale à la fonction), par ses propriétés algébriques (transforme une somme en produit), ou par son développement en série.

Par une équation différentielle

Définition —  On appelle fonction exponentielle l'unique fonction dérivable vérifiant l'équation différentielle et la condition initiale suivante :

f'=f \qquad f(0) = 1
Courbe d'équation y=exp(x) et quelques sous-tangentes

Si on note exp cette fonction, le processus de construction conduit à définir exp(x) par

\exp(x)=\lim_{n \to + \infty}\left(1+\frac xn\right)^n

Le nombre e égal à exp(1) est alors défini par

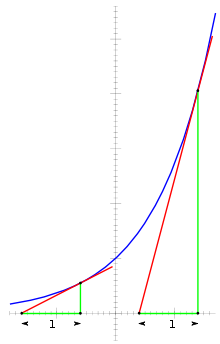
\mathrm e = \exp(1)=\lim_{n \to + \infty}\left(1+\frac 1n\right)^n

Cette propriété d'être sa propre dérivée se traduit par une propriété sur la sous-tangente à la courbe représentative de exp. La sous-tangente, c'est-à-dire la distance qui sépare le réel x de l'abscisse du point d'intersection de la tangente à la courbe au point d'abscisse x avec l'axe des x est constante et vaut 1.

On montre qu'une telle fonction transforme toujours une somme en produit, c'est-à-dire que, pour tout x et tout y,

\exp(x+y)=\exp(x)\cdot\exp(y)
Démonstration

On démontre qu'il existe une fonction f vérifiant ces conditions, que l'on construit grâce à la méthode d'Euler. On montre que f ne peut pas s'annuler, et que f est l'unique solution de l'équation différentielle.

Il existe une fonction f vérifiant ces conditions

L'approximation affine de la fonction f montre que, pour h petit, f(a + h) est voisin de f(a) + f'(a)h, c'est-à-dire de f(a)(1 + h). En partant de x0=1, en prenant pour h la valeur \scriptstyle \frac xn, et en appliquant l'approximation affine n fois, on arrive à dire que f(x) doit être voisin de \scriptstyle\left(1+ \frac xn\right)^n. L'idée est donc prendre pour valeur de f(x) , \scriptstyle \lim_{n \to + \infty}\left(1+\frac xn\right)^n. Encore faut-il montrer que cette expression a bien une limite pour tout n , que la fonction que l'on obtient est bien dérivable et égale à sa dérivée. On se sert pour cela des suites \scriptstyle \left (1+ \frac xn\right)^n et \scriptstyle\left(1- \frac xn\right)^{-n} que l'on prouve être adjacentes[1].

La fonction f ne peut pas s'annuler

On pose u(x)=f(x)\cdot f(-x) et l'on dérive
u'(x)=f'(x)\cdot f(-x)-f(x)f'(-x) = f(x)\cdot f(-x)-f(x)\cdot f(-x)=0
la fonction u est donc constante. L'égalité
u(0)=f(0)\cdot f(0)=1
assure que cette constante est non nulle, donc aucun des termes du produit n'est nul. f(x) ne s'annule pas.

La fonction f est l'unique solution au problème

On suppose qu'il existe une autre fonction g solution de l'équation et on étudie h=\frac {g}{f}
h'=\dfrac{g'f-gf'}{f^2}=\dfrac{gf-gf}{f^2}=0
car g et f vérifient g'=g et f'=f.
La fonction h est donc constante
h(0)=\frac{g(0)}{f(0)}=1
La fonction est donc constante égale à 1, ce qui assure que g = f

La propriété algébrique est conservée

On pose f2(x) = f(x + u) et l'on dérive
f2'(x) = f'(x + u) = f(x + u) = f2(x)
On pose alors h_2=\frac {f_2}{f} et par un raisonnement analogue, on montre que h2 est constante
h_2(0)=\frac{f_2(0)}{f(0)}=f(u)
donc \frac{f(x+u)}{f(x)}=f(u) soit encore f(x+u)=f(x)\cdot f(u).

La sous-tangente est constante

La tangente au point d'abscisse x a pour équation Y = exp(x)(X − x) + exp(x) et coupe l'axe des abscisses pour X vérifiant l'équation
\exp(x)(X-x)+\exp(x)=0 \Leftrightarrow X-x+1=0 \Leftrightarrow x-X=1

Caractérisation algébrique

Définition — la fonction exp est l'unique fonction continue de {}^\R dans {}^{\R^*} transformant une somme en produit, c'est-à-dire vérifiant l'équation fonctionnelle

\forall(u,v)\in\R : f(u+v)=f(u)\cdot f(v) .

et prenant la valeur e en 1

On détermine exp(x) sur les entiers puis sur les rationnels puis sur les irrationnels par continuité. Des égalités

  • \exp(n)=\mathrm e^n\,
  • \exp(p/q)=(\mathrm e^{1/q})^p=(\mathrm e^p)^{1/q} = \mathrm e^{p/q}\,

On en déduit la nouvelle notation de la fonction exp :

\exp(x)=\mathrm e^x\, pour tout réel x
Démonstration

On suppose qu'une fonction f vérifie ces propriétés et on montre qu'elle est alors entièrement déterminée.

La fonction f prend des valeurs toujours strictement positives :

On remarque que la relation
f(u)=f\left(2\frac u2\right) =\left[ f\left(\frac u2\right)\right]^2

assure que la fonction est toujours à valeurs dans l'ensemble des réels strictement positifs

f(0) vaut 1

f(u)=f(u+0)=f(u)\times f(0)

donne pour seule valeur possible pour f(0) la valeur 1 car f(u) ne peut être nul.

Calcul de f(n)

L'application de la propriété à une somme de n termes donne

f(nu)=f(u+u+\cdots + u) = f(u)\times f(u)\times\cdots \times f(u)=f(u)^n pour tout entier naturel n

Puis les égalités

f(nu)\times f(-nu)=1 et donc f(-nu)=\dfrac{1}{f(u)^n}=f(u)^{-n}

permettent de généraliser la propriété à tout entier relatif n;

Puisque f(1) = e, on a

f(n)=\mathrm e^n\, , pour tout n entier naturel puis relatif,

Calcul de f(r)

L'égalité, pour tout entier relatif p et entier naturel q non nul,

\mathrm e^p=f\left(q\frac pq\right)=\left(f\left(\frac pq\right)\right)^q

permet de déduire

f\left(\frac pq\right)= \sqrt[q]{\mathrm e^p} =(\mathrm e^p)^{1/q}

puis

f\left(\frac pq\right) = \left(f\left(\frac 1q\right)\right)^p=(\sqrt[q]{\mathrm e})^p=(\mathrm e^{1/q})^p=\mathrm e^{p/q}

Calcul de f(x)

La valeur de f(x) pour x irrationnel s'obtient par prolongement par continuité.

L'existence d'une telle fonction provient de la possibilité de prolonger par continuité une fonction définie sur {}^\Q à une fonction définie sur {}^\R en conservant ses propriétés algébriques. La construction prouve l'unicité de la fonction vérifiant l'équation fonctionnelle :

\forall(u,v)\in\R : f(u+v)=f(u)\cdot f(v)\qquad f(1)=\mathrm e.

À partir de la fonction logarithme népérien

Définition — La fonction exp est la bijection réciproque de la fonction logarithme népérien

En effet la fonction logarithme népérien étant continue strictement croissante sur son ensemble de définition, elle définit une bijection de {}^{\R^*_+} sur {}^\R. Sa réciproque est une fonction f définie sur {}^\R vérifiant f(0)=1 car ln(1)=0. La fonction ln étant dérivable et de dérivée non nulle, sa réciproque est une fonction dérivable et, pour tout x

f'(x)=\frac1{\ln'(f(x))}=f(x)

Par une série

La fonction exponentielle et son approximation par les premiers termes de la série

Enfin, en appliquant la méthode de recherche de solutions analytiques des équations différentielles linéaires, on peut définir l'application exponentielle exp  ou encore x\mapsto \mathrm e^x comme la somme d'une série entière de rayon de convergence infini :

\exp(x) = \sum_{n = 0}^{+\infty} {x^n \over n!},

où n! est la factorielle de n.

Comment trouver cette série ?

Supposons qu'il existe une solution analytique f somme d'une série entière de rayon de convergence R > 0, disons, pour fixer les notations :

f(x)=\sum_{n=0}^{+\infty}a_nx^n, avec a0 = 1.

La dérivée est donnée par :

f'(x)=\sum_{n=1}^{+\infty}n\cdot a_nx^{n-1}.

De fait, l'équation f'(x) = f(x) s'écrit, par unicité des coefficients dans le développement en séries entières :

a_n=(n+1)\cdot a_{n+1}.

Par une récurrence immédiate, on établit :

a_n=\frac{1}{n!}.

Il existe de nombreux développements en fraction continue de la fonction exponentielle. On peut citer l'exemple suivant :

\exp(x) = 1 + \frac{x\mid}{\mid 1} - \frac{\frac 12 x \mid}{\mid 1} + \frac{\frac 16x \mid}{\mid 1} - \frac{\frac 16x \mid}{\mid 1} + \frac{\frac 1{10}x \mid}{\mid 1} - \frac{\frac 1{10}x \mid}{\mid 1} + \frac{\frac 1{14}x \mid}{\mid 1} - \frac{\frac 1{14}x \mid}{\mid 1}+\cdots

Une analyse détaillée des expressions de cette nature est proposée dans l'article Approximant de Padé de la fonction exponentielle.

Étude de la fonction exponentielle

Représentation graphique de la fonction exponentielle dans \R

La fonction exp étant définie comme l'unique fonction égale à sa dérivée et prenant la valeur 1 en 0. On peut en étudier les caractéristiques.

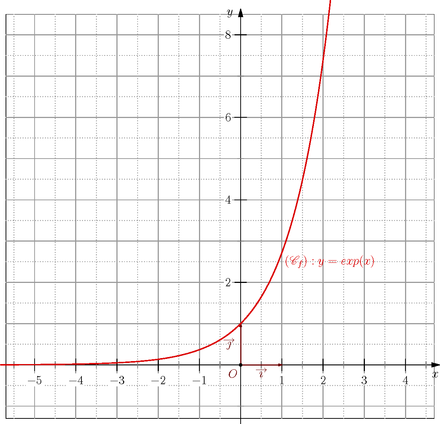
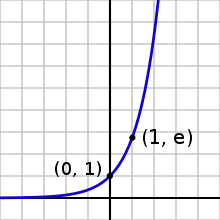
La fonction exp  prend en 1 une valeur irrationnelle qui est noté e et vaut environ 2,718.

Du fait de la continuité, supposée dans les trois définitions données, si x est réel, alors exp(x) est un réel strictement positif. D'autre part la fonction exp de {}^\R dans {}^{\R_+^*} est strictement croissante, continue, continûment dérivable, infiniment dérivable, et encore mieux analytique (c.-à-d. développable en séries entières au voisinage de tout point).

De plus,

\lim_{x\to -\infty}\exp(x)=0

et

\lim_{x\to +\infty}\exp(x)=+\infty,

elle admet donc une application réciproque, qui est la fonction logarithme népérien ln, définie sur \R_+^*.

La fonction exp  tend donc vers + ∞ quand sa variable tend vers + ∞ et ce plus rapidement que toute fonction polynôme, c'est-à-dire que

\lim_{x\to +\infty}\frac{\exp(x)}{x^n}=+\infty

quel que soit l'entier naturel n. De même on a

\lim_{x\to -\infty}x^n\exp(x)=0

Comme les dérivées successives de exp sont exp, la dérivée seconde est positive. Donc exp est convexe.

Propriétés

La fonction exponentielle transforme les sommes en produit, on en déduit

e0 = 1
e1 = e
\mathrm e^{x + y} = \mathrm e^x\cdot \mathrm e^y
\mathrm e^{nx} = \left( \mathrm e^x \right)^n, pour tout entier n
\frac 1{\mathrm e^x} = \left(\frac1e \right)^x = \mathrm e^{-x}
\mathrm e^{x/n} = \sqrt[n]{\mathrm e^x} , pour tout entier naturel n > 0

Elles sont valables pour tous réels x et y .

La fonction exponentielle est une bijection de \R sur \R_+^*, strictement croissante dont la bijection réciproque est la fonction logarithme népérien

pour tout réel x, \ln(\mathrm e^x)=x\,
pour tout réel x strictement positif, \mathrm e^{\ln(x)} = x\,
pour tout réel a et tout réel b strictement positif, \mathrm e^a=b \Leftrightarrow a=\ln(b)

Fonction exponentielle de base a

Article détaillé : Exponentielle de base a.

La propriété algébrique de la fonction exponentielle (fonction continue non nulle transformant une somme en produit) est partagée par un ensemble de fonctions qui portent aussi le nom de fonctions exponentielles. Elles sont entièrement déterminée dès que l'on a précisé leur valeur en 1 qui doit être un réel strictement positif. La fonction qui prend la valeur a en 1 est alors appelée fonction exponentielle de base a. On peut ainsi considérer que la fonction exponentielle est la fonction exponentielle de base e.

Toutes les fonctions exponentielles de base a s'expriment à l'aide de la fonction exp et de la fonction logarithme népérien

\exp_a(x)= a^x =\mathrm e^{x\ln(a)}\,

Généralisation à d'autres ensembles

Dans le plan complexe

Définitions

On peut définir la fonction \scriptstyle \exp complexe de deux façons :

  1. En utilisant la propriété :
    exp(ix) = cos(x) + isin(x),
    on écrit ;
    \exp(a + bi) = \exp(a) \cdot (\cos(b) + i \sin(b))
    où a et b sont des nombres réels.
  2. En utilisant le développement en série de l'exponentielle qui permet d'étendre celle-ci au plan complexe.
    \exp(z) = \sum_{n = 0}^{\infty} {z^n \over n!}

La fonction exponentielle vérifie alors les propriétés importantes suivantes, pour tous z et w :

exp(z + w) = exp(z)exp(w)
exp(0) = 1
\exp(z) \ne 0
\exp '(z) = \exp(z)\!

Ces formules se montrent à l'aide des formules de trigonométrie ou à l'aide de la notion de produit de Cauchy de deux séries selon le mode de définition de l'exponentielle.

La fonction exponentielle dans le plan complexe est une fonction holomorphe qui est périodique, de période imaginaire 2iπ.

La fonction exponentielle complexe s'exprime donc à l'aide de la fonction exponentielle réelle et des fonctions trigonométriques. Sa périodicité empêche la création d'une réciproque, c'est la raison pour laquelle prolonger le logarithme naturel à l'ensemble des nombres complexes, donne naturellement une fonction multiforme \scriptstyle z\mapsto \ln(z), appelée logarithme complexe.

L'exponentielle plus générale :

pour tous nombres complexes z et w, z^w = \exp(w\cdot \ln(z))

est alors aussi une fonction multiforme. Les propriétés ci-dessus des exponentielles restent vraies à condition de les interpréter convenablement comme des relations entre fonctions multiformes.

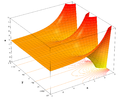
Représentations

Si \scriptstyle w = x+iy on peut représenter graphiquement, dans l'espace, les fonctions \scriptstyle w \mapsto \Re(\exp (w)), \scriptstyle w \mapsto \Im(\exp (w)), \scriptstyle w \mapsto |\exp (w)| et \scriptstyle w \mapsto \arg(\exp (w))

  • Surfaces représentant la partie réelle, la partie imaginaire, le module et l'argument principal de l'exponentielle complexe

  • \scriptstyle z=\Re(\exp(x+iy))

  • \scriptstyle z=\Im(\exp(x+iy))

  • \scriptstyle z=|\exp(x+iy)|

  • \scriptstyle z=\arg(\exp(x+iy))

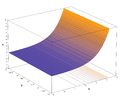
  • Courbe de densité représentant la partie réelle et la partie imaginaire de l'exponentielle complexe

  • \scriptstyle z=\Re(\exp(x+iy))

  • \scriptstyle z=\Im(\exp(x+iy))

Pour d'autres représentations de l'exponentielle à base e, se référer à l'article en anglais de wikimedia commons.

Fonctions exponentielles dans d'autres espaces

La définition de l'exponentielle comme série entière permet de définir l'exponentielle d'une matrice carrée \scriptstyle M comme

\exp(M)=\mathrm e^M=\sum_{k=0}^\infty{ 1\over k!}M^k.

Les exponentielles de matrices sont utiles dans la résolution des équations différentielles ordinaires.

Article détaillé : exponentielle de matrice.

La définition de l'exponentielle comme un morphisme continu d'un groupe additif vers un groupe multiplicatif permet de définir une fonction exponentielle de ℝ vers tout groupe topologique. Plus généralement, pour un groupe topologique G, on appelle sous-groupe à un paramètre tout morphisme continu ℝ→G. Certains ouvrages peuvent remplacer l'hypothèse de continuité par la mesurabilité.

Article détaillé : sous-groupe à un paramètre.

La définition de la fonction exponentielle comme solution d'une équation différentielle se généralise pour les groupes de Lie et les géodésiques dans les variétés riemanniennes

Article détaillé : application exponentielle.

La définition de l'exponentielle comme série entière permet de la définir sur des algèbres de Banach.

Applications

Équation différentielle linéaire

Article détaillé : équation différentielle linéaire.

L'importance majeure des fonctions exponentielles en sciences, provient du fait qu'elles sont proportionnelles à leur propre dérivée. a étant un nombre réel ou complexe, on a :

\frac {\mathrm d}{\mathrm d x}\lambda \mathrm e^{ax} = a \lambda \mathrm e^{ax}

ou plus exactement, la fonction \varphi : x\mapsto \lambda \mathrm e^{ax} est l'unique solution de l'équation fonctionnelle

φ' = aφ et φ(0) = λ

Si une grandeur croît ou décroît, en fonction du temps et que la vitesse de «sa course» est proportionnelle à «sa taille», comme dans le cas de la croissance d'une population, des intérêts composés continus ou de la décroissance radioactive, alors cette grandeur peut être exprimée comme une constante fois une fonction exponentielle du temps.

La fonction exponentielle de base e est solution de l'équation différentielle élémentaire :

y' = y

et on la rencontre fréquemment dans les solutions d'équations différentielles. En particulier, les solutions d'une équation différentielle linéaire peuvent être écrites à l'aide des fonctions exponentielles. On les trouve aussi dans les solutions des équations différentielles de Schrödinger, de Laplace ou dans l'équation différentielle du mouvement harmonique simple.

Fonction trigonométrique

Article détaillé : Fonction trigonométrique.

La fonction exponentielle est d'une utilité capitale en trigonométrie. Les formules d'Euler (que l'on démontre à partir de la définition exp(iz) = cos(z) + isin(z)) nous donnent un lien direct entre les fonction cosinus et sinus, réelles ou non, et la fonction exponentielle complexe.

\cos x = {\mathrm e^{ix} + \mathrm e^{-ix} \over 2}
\sin x = {\mathrm e^{ix} - \mathrm e^{-ix} \over 2i}

Ces formules permettent de retrouver la plupart des formules trigonométriques, en particulier

\cos(a+b)= \cos(a) \cos(b) -\sin(a) \sin(b) ~
\sin(a+b)= \sin(a) \cos(b) +\sin(b) \cos(a) ~

à partir desquelles on peut retrouver quasiment toutes les autres.

La fonction exponentielle est aussi un moyen facile (bien que les calculs puissent être longs) de linéariser des fonctions trigonométriques.

\cos^{n} x = \left(\frac{\mathrm e^{ix}+\mathrm e^{-ix}}{2}\right)^{n}
\sin^{n} x= \left(\frac{\mathrm e^{ix}-\mathrm e^{-ix}}{2i}\right)^{n}

Il suffit alors de développer la somme grâce à la formule du binôme de Newton, à regrouper les termes sachant que

ei(n − k)xe − ikx = ei(n − 2k)x
eimx + e − imx = 2cos(mx)
eimx − e − imx = 2isin(mx)

La fonction exponentielle trouve aussi son utilité quand on veut démontrer la formule de Moivre.

Fonction exponentielle et trigonométrie hyperbolique

À partir de la fonction exponentielle, on peut définir les fonctions de trigonométrie hyperbolique, définissant les fonctions hyperboliques cosinus hyperbolique, ch (ou cosh en anglais) et sinus hyperbolique, sh (ou sinh en anglais), utilisées en partie dans les résolutions des équations différentielles de second ordre.

Théorie de Fourier

Article détaillé : Théorie de Fourier.

Les fonctions exponentielles \scriptstyle t \mapsto e^{ikt} où t est un réel sont utilisées dans la théorie de Fourier. Elles permettent d'exprimer toute fonction périodique comme somme de fonctions trigonométriques, ce sont les séries de Fourier. Elles permettent aussi de définir la transformée de Fourier d'une fonction de carré sommable.

Notes et références

  1. ↑ Pour une démonstration détaillée, voir par exemple la démonstration de Gilles Constantini.

Voir aussi

Sur les autres projets Wikimedia :


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction exponentielle de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Fonction exponentielle­ — Exponentielle Pour les articles homonymes, voir Exp. Représentation graphique de la fonction exponentielle de base e (en noir), de base 10 (en rouge) et de base 1/2 (en bleu) …   Wikipédia en Français

  • fonction exponentielle — eksponentinė funkcija statusas T sritis fizika atitikmenys: angl. exponential function vok. exponentielle Funktion, f rus. экспоненциальная функция, f pranc. fonction exponentielle, f …   Fizikos terminų žodynas

  • Fonction exponentielle (mathématiques élémentaires) — Exponentielle Pour les articles homonymes, voir Exp. Représentation graphique de la fonction exponentielle de base e (en noir), de base 10 (en rouge) et de base 1/2 (en bleu) …   Wikipédia en Français

  • Fonction exponentielle de base a — ● Fonction exponentielle de base a fonction qui, lorsqu elle est définie sur R, est obtenue comme réciproque de la fonction logarithme de base a. (Notation : expa.) …   Encyclopédie Universelle

  • Fonction exponentielle étirée — Figure 1. Exemple d’ajustement par une exponentielle étirée (avec β=0,52) d’un ensemble de mesures. À titre de comparaison, le graphique montre aussi l’ajustement par une exponentielle simple et par une exponentielle double. Les données mesurent… …   Wikipédia en Français

  • Fonction exponentielle double —  Cet article concerne la fonction exponentielle double. L’expression « distribution exponentielle double » peut désigner la loi de Laplace, qui est une distribution exponentielle bilatérale ou la distribution de Gumbel qui est une… …   Wikipédia en Français

  • Approximant de Padé de la fonction exponentielle — Les travaux présentés dans cet article sont l œuvre d Henri Padé, un mathématicien français. En mathématiques, un approximant de Padé de la fonction exponentielle est une fraction rationnelle h(x) / k(x), où h(x) désigne un polynôme de degré p et …   Wikipédia en Français

  • EXPONENTIELLE ET LOGARITHME — Pour les constructeurs des premières tables, les logarithmes étaient avant tout un outil de calcul numérique; mais leur importance n’a cessé de croître. Il suffira de feuilleter cette encyclopédie pour constater que, de nos jours, les logarithmes …   Encyclopédie Universelle

  • Fonction KWW — Fonction exponentielle étirée Figure 1. Exemple d’ajustement par une exponentielle étirée (avec β=0,52) d’un ensemble de mesures. À titre de comparaison, le graphique montre aussi l’ajustement par une exponentielle simple et par une exponentielle …   Wikipédia en Français

  • Fonction de Kohlrausch-Williams-Watts — Fonction exponentielle étirée Figure 1. Exemple d’ajustement par une exponentielle étirée (avec β=0,52) d’un ensemble de mesures. À titre de comparaison, le graphique montre aussi l’ajustement par une exponentielle simple et par une exponentielle …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”