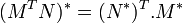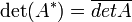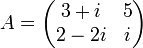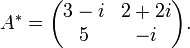Matrice Adjointe
- Matrice Adjointe
-
Matrice adjointe
En algèbre linéaire, une matrice adjointe (aussi appelée matrice transjuguée) d’une matrice M sur les complexes est la matrice transposée de la matrice conjuguée de M.
La matrice adjointe est traditionellement dénotée 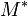 mais il arrive couramment de renconter d’autres notations :
mais il arrive couramment de renconter d’autres notations :
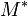 ou
ou 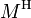 sont communément utilisés en algèbre linéaire, la seconde notation étant aussi appelée conjuguée hermitienne et plus fréquente dans le cas d’algèbres sur des espaces linéaires de fonctions ou de distributions (de dimension finie ou non).
sont communément utilisés en algèbre linéaire, la seconde notation étant aussi appelée conjuguée hermitienne et plus fréquente dans le cas d’algèbres sur des espaces linéaires de fonctions ou de distributions (de dimension finie ou non).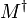 est la notation utilisée universellement en mécanique quantique, le plus souvent sur des algèbres de dimensions infinies, et souvent en association avec la notation bra et ket symbolisant les vecteurs d’états et matrices de transformation et simplifiant l’écriture et l’interprétation des expressions .
est la notation utilisée universellement en mécanique quantique, le plus souvent sur des algèbres de dimensions infinies, et souvent en association avec la notation bra et ket symbolisant les vecteurs d’états et matrices de transformation et simplifiant l’écriture et l’interprétation des expressions .- La notation
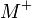 est parfois utilisée aussi, bien que ce symbole soit plutôt utilisé communément pour désigner le pseudo-inverse de Moore-Penrose.
est parfois utilisée aussi, bien que ce symbole soit plutôt utilisé communément pour désigner le pseudo-inverse de Moore-Penrose.
On a donc : 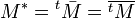 .
.
Note : L'expression matrice adjointe est parfois utilisée dans un sens différent pour désigner la comatrice. On utilise dans ce cas la notation adj(M).
Propriétés
Théorème de Binet-Cauchy :
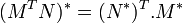
Autres propriétés
Si 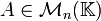 alors
alors
Exemple
Si :
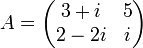
alors :
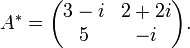
Voir aussi
|
Articles en rapport avec les matrices |
| Par forme |
|
| Transformée |
|
| En relation |
|
| Par propriété |
|
| Par famille |
|
| Particulière |
|
| Associée |
|
| Résultats |
|
| Voir aussi |
|
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Matrice Adjointe de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Matrice adjointe — En algèbre linéaire, une matrice adjointe (aussi appelée matrice transconjuguée) d’une matrice M à coefficients complexes est la matrice transposée de la matrice conjuguée de M. Dans le cas particulier où M est à coefficients réels, sa matrice… … Wikipédia en Français
matrice adjointe — jungtinė matrica statusas T sritis fizika atitikmenys: angl. adjoint matrix; conjugate matrix vok. adjungierte Matrix, f; konjugierte Matrix, f rus. присоединённая матрица, f; сопряжённая матрица, f pranc. matrice adjointe, f; matrice associée, f … Fizikos terminų žodynas
matrice adjointe — prijungtinė matrica statusas T sritis automatika atitikmenys: angl. adjoint matrix vok. adjungierte Matrix, f rus. присоединённая матрица, f pranc. matrice adjointe, f … Automatikos terminų žodynas
Matrice Normale — En algèbre linéaire, une matrice A est une matrice normale si elle vérifie l égalité suivante: A.A * = A * .A, avec A * la matrice adjointe de A. Toutes les matrices hermitiennes, anti hermitiennes, unitaires, symétriques, anti symétriques et… … Wikipédia en Français
Matrice Unitaire — En algèbre linéaire, une matrice A est une matrice unitaire si elle vérifie l égalité suivante: , avec A * la matrice adjointe de la matrice A et I la matrice identité. Par suite, les matrices unitaires sont donc inversibles, d inverse Voir aussi … Wikipédia en Français
Matrice congruente — En mathématiques, deux matrices carrées sont dites congruentes si elles représentent la même forme bilinéaire dans deux bases différentes. Si ces deux matrices sont notées A et B, cette condition peut s exprimer comme l existence d une matrice… … Wikipédia en Français
Matrice Conjuguée — Pour les articles homonymes, voir Conjugaison (homonymie). En algèbre linéaire, une matrice conjuguée d une matrice sur les complexes dénotée M est la transposée de la matrice formée des éléments de M conjugués. La matrice conjuguée est dénotée … Wikipédia en Français
Matrice conjuguee — Matrice conjuguée Pour les articles homonymes, voir Conjugaison (homonymie). En algèbre linéaire, une matrice conjuguée d une matrice sur les complexes dénotée M est la transposée de la matrice formée des éléments de M conjugués. La matrice… … Wikipédia en Français
Matrice antihermitienne — ● Matrice antihermitienne matrice carrée à éléments complexes qui est égale à l opposé de sa matrice adjointe … Encyclopédie Universelle
Matrice diagonalisable — Exemple de matrice diagonalisable sur le corps des complexes mais pas sur celui des réels, son polynôme caractéristique étant X2 + 1. En mathématiques, une matrice diagonalisable est une matrice carrée semblable à une matrice diagonale. Cette p … Wikipédia en Français
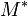 mais il arrive couramment de renconter d’autres notations :
mais il arrive couramment de renconter d’autres notations :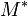 ou
ou 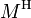 sont communément utilisés en algèbre linéaire, la seconde notation étant aussi appelée conjuguée hermitienne et plus fréquente dans le cas d’algèbres sur des espaces linéaires de fonctions ou de distributions (de dimension finie ou non).
sont communément utilisés en algèbre linéaire, la seconde notation étant aussi appelée conjuguée hermitienne et plus fréquente dans le cas d’algèbres sur des espaces linéaires de fonctions ou de distributions (de dimension finie ou non).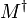 est la notation utilisée universellement en mécanique quantique, le plus souvent sur des algèbres de dimensions infinies, et souvent en association avec la notation bra et ket symbolisant les vecteurs d’états et matrices de transformation et simplifiant l’écriture et l’interprétation des expressions .
est la notation utilisée universellement en mécanique quantique, le plus souvent sur des algèbres de dimensions infinies, et souvent en association avec la notation bra et ket symbolisant les vecteurs d’états et matrices de transformation et simplifiant l’écriture et l’interprétation des expressions .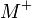 est parfois utilisée aussi, bien que ce symbole soit plutôt utilisé communément pour désigner le pseudo-inverse de Moore-Penrose.
est parfois utilisée aussi, bien que ce symbole soit plutôt utilisé communément pour désigner le pseudo-inverse de Moore-Penrose.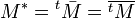 .
.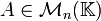 alors
alors