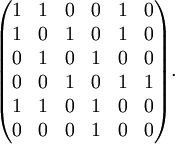Matrice D'adjacence

Matrice d'adjacence

En mathématiques, une matrice d'adjacence pour un graphe fini $G$ à n sommets est une matrice de dimension n × n dont l'élément non-diagonal a_ij est le nombre d'arêtes liant le sommet $i$ au sommet $j$ . L'élément diagonal a_ii est le nombre de boucles au sommet $i$ (ou deux fois ce nombre, selon certains usages).

Cet outil mathématique est très utilisé en informatique, mais intervient aussi naturellement dans les chaînes de Markov. En particulier, la probabilité limite s'interprète comme un vecteur propre.

Définition

Supposez que $G = (V, E)$ est un graphe simple, où 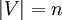$\left|V\right|=n$ . Supposez aussi que les sommets de $G$ sont, arbitrairement, 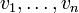$v_1,\ldots,v_n$ . La matrice d’adjacence $A$ de $G$ se rapportant à cet ensemble de sommets est la matrice 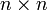$n\times n$ booléenne $A$ avec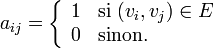

$a_{ij}=\left\{\begin{array}{rl} 1 & \mbox{si } (v_i,v_j)\in E \\ 0 & \mbox{sinon.} \end{array}\right.$

Une matrice d’adjacence d’un graphe est fondée sur la relation d’ordre établie pour les sommets.

Donc, il existe (au plus) $n!$ matrices d’adjacences différentes pour un graphe comportant $n$ sommets puisqu’il y a $n!$ possibilités d’ordonner ces sommets.

Propriétés

Une fois que l'on fixe l'ordre des sommets, il existe une matrice d'adjacence unique pour chaque graphe. Celle-ci n'est la matrice d'adjacence d'aucun autre graphe. Dans le cas particulier d'un graphe simple et fini, la matrice d'adjacence est une matrice binaire avec des zéros sur la diagonale. Si le graphe n'est pas orienté, la matrice d'adjacence est symétrique, ce qui veut dire que $a i j = a j i$ .

Exemple

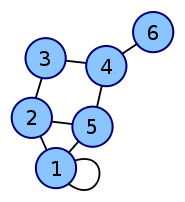
La matrice d'adjacence du graphe étiqueté suivant

est

$\begin{pmatrix} 1 & 1 & 0 & 0 & 1 & 0\\ 1 & 0 & 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 & 1 & 1\\ 1 & 1 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ \end{pmatrix}.$

Remarque

Si $A$ est la matrice d'adjacence d'un graphe fini $G$ dont les sommets sont numérotés de $1$ à $n$ , le nombre de chemins de longueur exactement $k$ allant de $i$ à $j$ est le coefficient en position $(i, j)$ de la matrice $A k$ — ceci si chaque arrête entre deux sommets à une longueur égale à 1.

Voir aussi

Théorie des graphes

Portail des mathématiques

Ce document provient de « Matrice d%27adjacence ».

Catégories : Structure de données en théorie des graphes | Matrice remarquable | Probabilités

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice D'adjacence de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Matrice d'adjacence — En mathématiques, une matrice d adjacence pour un graphe fini G à n sommets est une matrice de dimension n × n dont l élément non diagonal aij est le nombre d arêtes liant le sommet i au sommet j. L élément diagonal aii est le nombre de boucles… … Wikipédia en Français
Matrice Laplacienne — En théorie des graphes, une matrice laplacienne, ou matrice de Laplace, est une matrice représentant un graphe. Définition La matrice laplacienne d un graphe G non orienté et non réflexif est définie par : Ml = Md − Ma où Md est la matrice… … Wikipédia en Français
Matrice laplacienne — En théorie des graphes, une matrice laplacienne, ou matrice de Laplace, est une matrice représentant un graphe. Définition La matrice laplacienne d un graphe G non orienté et non réflexif est définie par : Ml = Md − Ma où Md est la matrice… … Wikipédia en Français
Matrice binaire — Définition Une matrice binaire est une matrice dont les coefficients sont soit 0, soit 1. En général ces coefficients sont les nombres de l Algèbre de Boole (logique) dans laquelle on appelle B l ensemble constitué de deux éléments appelés… … Wikipédia en Français
Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D … Wikipédia en Français
Matrice Définie Positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou complexes : aT désigne la… … Wikipédia en Français
Matrice Inversible — En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In suffit d aprés le… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Matrice D'adjacence