Caracteristique d'un anneau

Caracteristique d'un anneau

Caractéristique d'un anneau

Page d'aide sur l'homonymie Pour les articles homonymes, voir Caractéristique.

En algèbre, la caractéristique d'un anneau unitaire A est par définition l'ordre pour la loi additive de l'élément neutre de la loi multiplicative.

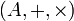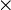On note, pour un anneau unitaire[1] (A, + ,\times), 0A l'élément neutre de «  +  » et 1A celui de « \times ».

La caractéristique d'un anneau 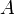\ A est donc le plus petit entier naturel non-nul 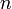\ n tel que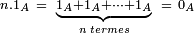 \scriptstyle{\ n.1_A~=~\underbrace{\scriptstyle 1_A+1_A+\cdots+1_A }_{n\; termes}~=~0_A}
Si un tel entier n'existe pas, on dit que la caractéristique est nulle (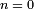\scriptstyle \ n\; = \; 0).

Sommaire

L'homomorphisme de Z dans A

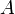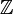Il existe un unique homomorphisme d'anneaux unitaires f de \mathbb{Z} dans \ A~ ( ~ \mathbb{Z} \; est en effet un objet initial de la catégorie des anneaux). Par définition, si n est un nombre entier strictement positif, on a :

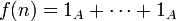f(n)=1_A+\cdots+1_A\,,

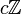où 1A est répété n fois. Comme \mathbb{Z} est un anneau euclidien, le noyau de f est principal et, par définition, la caractéristique de A est son générateur positif. Plus explicitement, c'est l'unique nombre entier positif ou nul c tel que le noyau de f soit l'idéal c\mathbb{Z}.

Propriétés sur les anneaux

En effet, si la caractéristique d'un anneau unitaire A est un entier non nul p > 0 divisible, elle peut s'écrire : 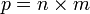p = n \times m où n et m sont strictement supérieurs à 1. En reprenant les notations ci-dessus, comme f est un homomorphisme d'anneaux, 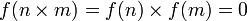f(n\times m)=f(n)\times f(m)=0. Si A est intègre, l'un des facteurs f(n) ou f(m) est nul. Cela contredit la définition de p, qui, comme générateur positif du noyau de f est le plus petit entier positif annulé par f. Donc p n'est pas divisible, il est premier.

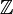  • Si la caractéristique d'un anneau est nulle, celui-ci est infini, car il contient un sous-anneau isomorphe à \mathbb Z .

L'homomorphisme f est injectif. Il induit un isomorphisme sur son image qui est un sous-anneau unitaire.

  • Si B est un sous-anneau unitaire de A, alors A et B ont même caractéristique.

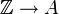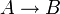L'homomorphisme \mathbb Z\rightarrow A se factorise évidemment à travers l'inclusion A\rightarrow B.

  • Pour tout homomorphisme d'anneaux unitaires 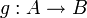g:A\rightarrow B, la caractéristique de B divise celle de A.

En effet, la composée des homomorphismes g.f est l'unique homomorphisme d'anneaux unitaires 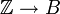\mathbb Z\rightarrow B. Son noyau est l'image réciproque par f du noyau de g. Il contient notamment le noyau de f. Si p et q sont les caractéristiques de A et de B, q Z contient p Z. Donc, q divise p.

  • Si A est un anneau commutatif, et si sa caractéristique est un nombre premier p, alors pour tous éléments x,y dans A, on a (x + y)p = xp + yp. L'application définie par f(x) = xp est un endomorphisme d'anneau injectif appelé endomorphisme de Frobenius.

Le résultat découle immédiatement de la formule de Newton et de ce que p divise dans Z les coefficients binomiaux apparaissant dans le développement.

Propriétés sur les corps

  • Si un corps K est de caractéristique nulle, il contient une copie de Q. S'il est de caractéristique p, il contient une copie de Z/pZ

Comme pour tout anneau intègre, la caractéristique de K est soit nulle soit un nombre premier p. Dans le premier cas, l'unique homomorphisme d'anneaux unitaires 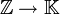\mathbb Z \rightarrow \mathbb K est injectif ; comme K est un corps, il induit une injection du corps des fractions de Z, à savoir le corps des rationnels Q (par définition des rationnels). Dans le deuxième cas, l'unique homomorphisme d'anneaux unitaires 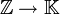\mathbb Z \rightarrow \mathbb K induit une injection de Z/pZ dans K. Or, comme p est premier, Z/pZ est un corps fini ; c'est l'unique corps fini Fp à p éléments.

  • Tout corps fini a pour cardinal une puissance d'un nombre premier, qui en est sa caractéristique.

Si K est un corps fini, pour des raisons de cardinalité, il ne peut pas contenir une copie de Q. Par ce qui précède, il est de caractéristique finie p et contient donc une copie du corps Fp. De fait, K est un espace vectoriel sur Fp ; sa dimension est nécessairement finie. Donc son cardinal est p à la puissance sa dimension.

  • Il existe des corps infinis possédant une caractéristique non nulle p, celle-ci étant un nombre premier.

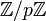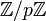C'est le cas par exemple du corps des fonctions rationnelles sur \mathbb Z/p\mathbb Z ou de la clôture algébrique de \mathbb Z/p\mathbb Z.

En effet, l'unique homomorphisme 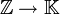\mathbb Z \rightarrow \mathbb K est croissant. Tout entier strictement positif est envoyé sur un élément strictement positif du corps, a fortiori différent de 0.

C'est donc le cas des corps des nombres rationnels \mathbb Q, et donc de ceux des nombres réels \R et complexes \mathbb C (puisque \mathbb Q est un sous-anneau de ces deux anneaux).

Références

Ouvrages

Notes

  1. ↑ Le cas de l'anneau nul est exclu, donc 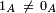\scriptstyle 1_A ~ \neq ~ 0_A ~, c'est-à-dire : la caractéristique n'est pas égale à 1.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Caract%C3%A9ristique d%27un anneau ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Caracteristique d'un anneau de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Caractéristique D'un Anneau — Pour les articles homonymes, voir Caractéristique. En algèbre, la caractéristique d un anneau unitaire A est par définition l ordre pour la loi additive de l élément neutre de la loi multiplicative. On note, pour un anneau unitaire[1] …   Wikipédia en Français

  • Caractéristique d'un anneau — Pour les articles homonymes, voir Caractéristique. En algèbre, la caractéristique d un anneau (unitaire) A est par définition l ordre pour la loi additive de l élément neutre de la loi multiplicative, si cet ordre est fini. On note, pour un… …   Wikipédia en Français

  • Caractéristique d'un anneau unitaire — ● Caractéristique d un anneau unitaire plus petit entier naturel n tel que ne = 0, e étant élément unité de l anneau et 0 élément neutre. (Un anneau de caractéristique n est isomorphe à l anneau Z°nZ. L anneau Z est de caractéristique nulle.) …   Encyclopédie Universelle

  • Caractéristique d'un corps — Caractéristique d un anneau Pour les articles homonymes, voir Caractéristique. En algèbre, la caractéristique d un anneau unitaire A est par définition l ordre pour la loi additive de l élément neutre de la loi multiplicative. On note, pour un… …   Wikipédia en Français

  • caractéristique — [ karakteristik ] adj. et n. f. • 1550; gr. kharaktêristikos I ♦ Adj. 1 ♦ Qui constitue un élément distinctif reconnaissable. Différence, élément, marque, propriété, signe, trait caractéristique. ⇒ déterminant, distinctif, essentiel, particulier …   Encyclopédie Universelle

  • Anneau Z/nZ — En mathématiques, et plus particulièrement en algèbre, Z/nZ est un cas particulier d anneau. Tout anneau unitaire contient soit un sous anneau isomorphe à Z/nZ soit à Z l anneau des entiers. Cet anneau joue un rôle particulier en arithmétique, il …   Wikipédia en Français

  • Anneau (Mathématiques) — Pour les articles homonymes, voir Anneau. En algèbre générale, un anneau est une structure algébrique sur laquelle deux opérations satisfont certaines des propriétés de l addition et la multiplication des nombres. Sommaire 1 Aspect historique …   Wikipédia en Français

  • Caracteristique — Caractéristique Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • Caracteristique (homonymie) — Caractéristique (homonymie) Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. De manière générale, le terme caractéristique désigne un élément qui permet de distinguer des objets ou des êtres de nature… …   Wikipédia en Français

  • Caractéristique (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. De manière générale, le terme caractéristique désigne un élément qui permet de distinguer des objets ou des êtres de nature semblable. En mathématiques,… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”