Matrice de Jones

Matrice de Jones

Formalisme de Jones

Page d'aide sur l'homonymie Pour les articles homonymes, voir Jones.

Le formalisme de Jones est un formalisme matriciel permettant de décrire l'état de polarisation de la lumière, ou de manière générale d'une onde électromagnétique, et son évolution à travers un système optique. Ce formalisme doit son nom à son inventeur Robert C. Jones qui le définit en 1941[1]. Dans ce formalisme, on représente la lumière polarisée par un vecteur de Jones et les éléments optiques linéaires sont représentés par des matrices de Jones. Le vecteur de Jones de la lumière en sortie du système est donnée par le produit de la matrice de Jones du système par le vecteur de Jones de la lumière d'entrée.

Ce formalisme n'est utile que pour la lumière totalement polarisée. Pour décrire la lumière incohérente et partiellement polarisée, on utilise les vecteurs de Stokes et les matrices de Mueller.

Sommaire

Définition

Le vecteur de Jones pour une onde polarisée se propageant suivant un axe z est défini par 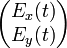\begin{pmatrix} E_x(t) \\ E_y(t)\end{pmatrix} ou Ex(t) et Ey(t) sont les composantes du champ électrique de l'onde selon les axes x et z. Habituellement, on normalise le vecteur à 1. Ceci empêche de traiter les problèmes d'absorption, mais simplifie souvent l'analyse par ailleurs. Une autre convention est de faire en sorte que le premier coefficient du vecteur soit un nombre réel. Ceci peut empêcher la prise en compte d'une différence de phase, et donc le calcul d'interférences entre plusieurs ondes.

Le tableau suivant donne des exemples de vecteurs de Jones normés.

Polarisation Vecteur de Jones correspondant
Rectiligne selon l'axe x 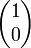\begin{pmatrix} 1 \\ 0 \end{pmatrix}
Rectiligne selon l'axe y 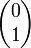\begin{pmatrix} 0 \\ 1 \end{pmatrix}
Rectiligne selon un axe à 45° par rapport à l'axe x 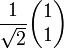\frac{1}{\sqrt2} \begin{pmatrix} 1 \\ 1 \end{pmatrix}
Circulaire droite 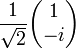\frac{1}{\sqrt2} \begin{pmatrix} 1 \\ -i \end{pmatrix}
Circulaire gauche 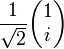\frac{1}{\sqrt2} \begin{pmatrix} 1 \\ i \end{pmatrix}

Le tableau suivant donne des exemples de matrices de Jones.

Système optique Matrice de Jones correspondante
Polariseur avec axe horizontal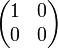

\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}
Polariseur avec axe vertical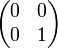

\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}
Polariseur avec axe incliné à 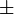\pm45°

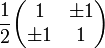
\frac12 \begin{pmatrix} 1 & \pm 1 \\ \pm 1 & 1 \end{pmatrix}
Polariseur incliné d'un angle \varphi

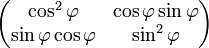
\begin{pmatrix} \cos^2\varphi & \cos\varphi\sin\varphi \\ \sin\varphi\cos\varphi & \sin^2\varphi \end{pmatrix}
Polariseur circulaire gauche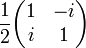

\frac12 \begin{pmatrix} 1 & -i \\ i & 1 \end{pmatrix}
Polariseur circulaire droit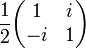

\frac12 \begin{pmatrix} 1 & i \\ -i & 1 \end{pmatrix}
Lame demi-onde avec l'axe rapide horizontal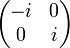

\begin{pmatrix} -i & 0 \\ 0 & i \end{pmatrix}
Lame quart d'onde avec axe rapide horizontal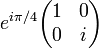

e^{i\pi /4} \begin{pmatrix} 1 & 0 \\ 0 & i \end{pmatrix}

Si un système optique est tourné autour de l'axe optique d'un angle θ, la matrice de Jones pour le système tourné M(θ) est obtenue à partir de la matrice du système non tourné par la transformation :

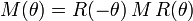M(\theta )=R(-\theta )\,M\,R(\theta ) ,
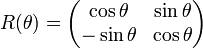où R(\theta ) = \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix} .

Notes et références

  1. ↑ R. C. Jones, "New calculus for the treatment of optical systems," J. Opt. Soc. Am. 31, 488–493, (1941)

(en) Cet article est partiellement ou en totalité issu d’une traduction de l’article en anglais intitulé « Jones Calculus ».

Bibliographie

  • (en) E. Collett, Field Guide to Polarization, SPIE Field Guides vol. FG05, SPIE (2005). ISBN 0-8194-5868-6.
  • (en)E. Hecht, Optics, 2nd ed., Addison-Wesley (1987). ISBN 0-201-11609-X.
  • (en) Frank L. Pedrotti, S.J. Leno S. Pedrotti, Introduction to Optics, 2nd ed., Prentice Hall (1993). ISBN 0-13-501545-6

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Formalisme de Jones ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice de Jones de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Matrice de Mueller — La matrice de Mueller est une matrice à 4 lignes et 4 colonnes, introduite par Hans Mueller dans les années 1940, pour manipuler les vecteurs de Stokes qui représentent la polarisation de la lumière incohérente. Sommaire 1 Description 1.1 Région… …   Wikipédia en Français

  • Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice De Mueller — La matrice de Mueller est une matrice à 4 lignes et 4 colonnes, introduite par Hans Mueller dans les années 1940, pour manipuler les vecteurs qui représentent la polarisation de la lumière incohérente. Sommaire 1 Matrice de Muller 1.1 Région… …   Wikipédia en Français

  • Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice de Muller — Matrice de Mueller La matrice de Mueller est une matrice à 4 lignes et 4 colonnes, introduite par Hans Mueller dans les années 1940, pour manipuler les vecteurs qui représentent la polarisation de la lumière incohérente. Sommaire 1 Matrice de… …   Wikipédia en Français

  • Matrice de mueller — La matrice de Mueller est une matrice à 4 lignes et 4 colonnes, introduite par Hans Mueller dans les années 1940, pour manipuler les vecteurs qui représentent la polarisation de la lumière incohérente. Sommaire 1 Matrice de Muller 1.1 Région… …   Wikipédia en Français

  • Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D …   Wikipédia en Français

  • Matrice Définie Positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou complexes : aT désigne la… …   Wikipédia en Français

  • Matrice Inversible — En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In suffit d aprés le… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”