Matrice Aléatoire

Matrice Aléatoire

Matrice aléatoire

Une matrice aléatoire est une matrice dont les éléments sont des variables aléatoires.

Face à la complexité croissante des spectres nucléaires observés expérimentalement dans les années 1950, Wigner a suggeré de remplacer l'opérateur hamiltonien du noyau par une matrice aléatoire. Cette hypothèse féconde a conduit au développement rapide d'un nouveau champ de recherche très actif en physique théorique, qui s'est propagé à la théorie des nombres en mathématiques, avec notamment une connexion intéressante avec la fonction zeta de Riemann. En plus de ces exemples on compte parmi les applications de la théorie des matrices aléatoires les systèmes intégrables, le chaos quantique, la gravité quantique en deux dimensions et plus via la théorie des cordes, la QCD sur réseau, les théories de jauge supersymétriques.

Sommaire

Quelques ensembles de matrices aléatoires

Ensembles gaussiens

Ce sont les ensembles introduits par Wigner pour la théorie des spectres nucléaires. On distingue trois ensembles :

  • l'ensemble gaussien orthogonal pour les systèmes invariants par renversement du temps (GOE),
  • l'ensemble gaussien unitaire pour les systèmes non-invariants par renversement du temps (GUE),
  • et l'ensemble gaussien symplectique pour les systèmes avec spin (GSE).

Dans le cas de l'ensemble GOE, on considère des matrices symétriques réelles 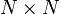N\times N dont les élements de matrices Aij obéissent à la distribution gaussienne :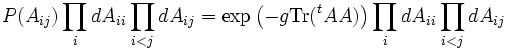

P(A_{ij})\prod_i dA_{ii} \prod_{i<j} dA_{ij} = \exp\left(-g \mathrm{Tr}({}^t A A)\right) \prod_i dA_{ii} \prod_{i<j} dA_{ij}

La distribution est invariante par les transformations orthogonales. De même, dans l'ensemble unitaire, on considère des matrices hermitiennes, et la distribution est invariante par les transformations unitaires. Dans l'ensemble GSE, la distribution est invariante sous l'action des transformations symplectiques.

Wigner a déduit la distribution des valeurs propres de ces matrices dans la limite 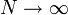N \to \infty . C'est la loi du demi-cercle.

Il est possible de déduire la loi de distribution jointe des valeurs propres par un changement de base. Le résultat est que : 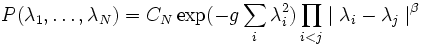P(\lambda_1,\ldots,\lambda_N) = C_N \exp(-g \sum_i \lambda_i^2) \prod_{i<j} \mid \lambda_i -\lambda_j \mid^\beta où les λi sont les valeurs propres de la matrice, et β = 1 dans le cas GOE, β = 2 dans le cas GUE, β = 4 dans le cas GSE.

A partir de ces distributions, on peut obtenir la loi de distribution des écarts entre valeurs propres. On montre que si s est la distance (normalisée par la densité d'états) entre deux valeurs propres, la probabilité que deux valeurs propres soient distantes de s tend vers zéro si s tend vers zéro. Si les valeurs propres étaient uniformément distribuées, cette probabilité serait donnée par la loi de Poisson et ne tendrait pas vers zéro pour s tendant vers zéro. Cette propriété des ensembles gaussiens est appelée répulsion des niveaux.

Ensembles unitaires

Notés COE, CUE, CSE. Cette fois, les matrices sont respectivement orthogonales, unitaires ou symplectiques. Leurs valeurs propres sont des nombres complexes de module 1. F. J. Dyson a montré que l'étude de la distribution de ces valeurs propres se ramenait à l'étude de la mécanique statistique d'un gaz de particules sur un cercle avec une interaction logarithmique avec la distance.

Applications de la théorie des matrices aléatoire

On présente brièvement dans les quelques paragraphes qui vont suivre quelques unes des applications modernes de la théorie des matrices aléatoires dans les domaines de la physique statistique, de la physique des particules, de la gravité quantique et des mathématiques pures.

Articles liés

Bibliographie

  • Madan Lal Mehta ; On the statistical properties of the level-spacings in nuclear spectra, Nuclear Physics 18 (1960), 395-419.
  • M.L. Mehta ; Random matrices. Cette « bible » a fait l'objet de trois éditions de volumes croissants :
    • Random Matrices and the Statistical Theory of Energy Levels, Academic Press (New York - 1967), 259 pp.
    • Random Matrices (2e edition révisée et augmentée), Academic Press (New York, San Diego - 1991), 562 pp.
    • Random matrices (3e edition), Pure and Applied Mathematics Series 142, Elsevier (London - 2004), 688 pp. ISBN 0120884097
  • M.L. Mehta ; Random matrices in nuclear physics and number theory, dans : J.E. Cohen, H. Kesten et C.M. Newman (eds.) ; Proceedings of the AMS-IMS-SIAM Joint Summer Conference, Bowdoin College, Brunswick, Maine, USA (June 1984), Contemporary Mathematics 50 (1986), 295-309.
  • E. Brézin, V.A. Kazakov, D. Serban, P.B. Wiegmann et A. Zabrodin (eds.)  ; Applications of Random Matrices in Physics, dans : Proceedings of the NATO Advanced Study Institute / Les Houches Summer School, June 6-25 2004, Les Houches (France), NATO Science Series II Vol. 221, Springer-Verlag, (Berlin - 2006). (ISBN 1-4020-4529-8)
  • B Eynard ; An introduction to Random Matrices, notes d'un cours donné au Service de Physique Théorique du CEA (Saclay - September 2000). Texte complet disponible ici.
  • Pierre Cartier, Bernard Julia, Pierre Moussa & Pierre Vanhove (eds.) ; Frontiers in Number Theory, Physics & Geometry (I) - On Random Matrices, Zeta Functions & Dynamical Systems, Les Houches Lectures Notes, Springer-Verlag (2006), ISBN 3-540-23189-7.
  • Philippe Di Francesco, Paul Ginsparg, Jean Zinn-Justin, 2D Gravity and Random Matrices., Phys.Rept. 254 (1995) 1-133, préprint disponible sur l'arXiv. (Une très bonne introduction au sujet.)
  • Malyshev, V.A., Vershik, A.M. (Eds.) ; Asymptotic combinatorics with applications to mathematical physics, dans : Proceedings of the NATO Advanced Study Institute, held in St.Petersburg, Russia, 9-22 July 2001, NATO Science Series II Vol. 77, Springer-Verlag, (ISBN 1-4020-0792-2)

Liens externes

  • Portail des mathématiques Portail des mathématiques
  • Portail de la physique Portail de la physique
Ce document provient de « Matrice al%C3%A9atoire ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice Aléatoire de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Matrice aleatoire — Matrice aléatoire Une matrice aléatoire est une matrice dont les éléments sont des variables aléatoires. Face à la complexité croissante des spectres nucléaires observés expérimentalement dans les années 1950, Wigner a suggeré de remplacer l… …   Wikipédia en Français

  • Matrice aléatoire —  Ne pas confondre avec la notion de matrice stochastique. Une matrice aléatoire est une matrice dont les éléments sont des variables aléatoires. Face à la complexité croissante des spectres nucléaires observés expérimentalement dans les… …   Wikipédia en Français

  • Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire …   Wikipédia en Français

  • Matrice stochastique —  Ne pas confondre avec la notion de matrice aléatoire. En mathématiques, une matrice stochastique (aussi appelée matrice de Markov) est une matrice carrée dont chaque élément est un réel compris entre 0 et 1 et dont la somme des éléments de… …   Wikipédia en Français

  • Matrice De Variance-Covariance — Une matrice de variance covariance est une matrice carrée caractérisant les interactions (linéaires) entre p variables aléatoires . Sommaire 1 Définition 2 Propriétés …   Wikipédia en Français

  • Matrice de covariance — Matrice de variance covariance Une matrice de variance covariance est une matrice carrée caractérisant les interactions (linéaires) entre p variables aléatoires . Sommaire 1 Définition 2 Propriétés …   Wikipédia en Français

  • Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D …   Wikipédia en Français

  • Matrice Définie Positive — En algèbre linéaire, la notion de matrice définie positive est analogue à celle de nombre réel strictement positif. On introduit tout d abord les notations suivantes ; si a est une matrice à éléments réels ou complexes : aT désigne la… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”