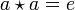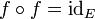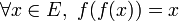Involution (mathematiques)

Involution (mathematiques)

Involution (mathématiques)

Page d'aide sur l'homonymie Pour les articles homonymes, voir Involution.

En mathématiques, une involution est une opération qui est son propre inverse.

Sommaire

Définition formelle

Soit M un monoïde, dont la loi de composition interne est notée 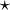\star et l'élément neutre noté e. On dit que 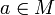a \in M est une involution si et seulement si

a \star a =e

L'un des cas fréquents est une involution dans un anneau par rapport à la deuxième loi.

Application involutive

L'un des cas fréquent d'involution porte sur les applications. Dans ce cas si f est une application d'un ensemble E dans lui-même, alors on dit que f est une involution ou une application involutive si et seulement si

f \circ f = \mathrm{id}_E

où idE est l'application identité sur E.

On "retombe" sur un élément après lui avoir appliqué deux fois de suite notre fonction. On a donc

\forall x \in E,\ f(f(x))=x

Propriétés

Une involution admet un inverse : elle-même. Les applications involutives sont des bijections.

Si 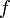\ f est une involution sur E, et si 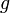\ g est une bijection de E vers F, de fonction inverse 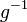\ g^{-1}, alors 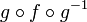g \circ f \circ g^{-1} est une involution sur F.

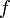\ f étant une involution sur E, si 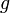\ g est une bijection sur E telle que 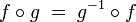f \circ g \; = \; g^{-1} \circ f \; , alors 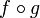f \circ g \; est une involution sur E.

Exemples

  • Pour tout 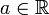a \in \R, la fonction 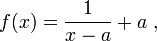f(x)= \frac{1}{x-a}+a \; , définie sur 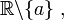\R \mathcal{n} \{a\} \; , est une involution.
  • Pour tout 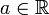a \in \R, la fonction 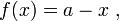f(x)= a-x \; , définie sur 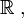\R \; , est une involution.
  • L'application identité est involutive.
  • Les symétries du plan constituent un exemple d'applications involutives.
  • En arithmétique, la multiplication par -1 est aussi une involution.
  • Une permutation est une involution si et seulement si elle se décompose en cycles disjoints de longueurs inférieures ou égales à 2.
  • La conjugaison des nombres complexes est un automorphisme involutif.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Involution (math%C3%A9matiques) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Involution (mathematiques) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Involution (mathématiques) — Pour les articles homonymes, voir Involution. En mathématiques, une involution est une opération qui est sa propre inverse. Sommaire 1 Définition formelle 2 Applicati …   Wikipédia en Français

  • Involution — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En mathématiques, une involution est une opération qui est son propre inverse. En médecine, une involution est une régression spontanée ou provoquée d un… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • GROUPES (mathématiques) - Groupes classiques et géométrie — Jusque vers 1800, la géométrie dite «élémentaire» est restée à peu de chose près ce qu’elle était dans l’Antiquité, tant dans sa substance que dans ses méthodes (l’invention de la «géométrie analytique» ayant à peu près exclusivement servi à… …   Encyclopédie Universelle

  • GROUPES (mathématiques) - Groupes de Lie — La théorie des groupes de Lie, fondée dans la période de 1870 1880 par le mathématicien norvégien Sophus Lie, a d’abord été considérée comme une partie assez marginale des mathématiques, liée à des problèmes touchant les équations différentielles …   Encyclopédie Universelle

  • GROUPES (mathématiques) - Groupes finis — Née de l’étude des groupes de permutations des racines d’équations, la théorie des groupes finis s’est développée indépendamment depuis le Traité des substitutions et des équations algébriques (1870) de Camille Jordan. Après les travaux… …   Encyclopédie Universelle

  • Symétrie centrale (mathématiques élémentaires) — Symétrie centrale La symétrie centrale est une transformation géométrique. Elle se fait autour d un point (O par exemple) , et qui transforme un point objet M en un point image M . De facon a ce que O soit le milieu du segment MM . On dit alors… …   Wikipédia en Français

  • Algèbre involutive simple — En mathématiques, une algèbre involutive simple sur un corps commutatif est une algèbre involutive qui n admet par d idéaux stable par l involution autre que {0} et elle même. Les algèbres involutives simples centrales (en un sens à préciser plus …   Wikipédia en Français

  • GÉOMÉTRIE — La géométrie est communément définie comme la science des figures de l’espace. Cette définition un peu incertaine risque de conduire à inclure dans la géométrie des questions qui ne sont géométriques que dans leur langage, mais relèvent en fait… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”