Matrice De Contrôle

Matrice De Contrôle

Matrice de contrôle

Une matrice de contrôle est un concept de théorie des codes utilisé dans le cas des codes correcteurs linéaires.

Elle correspond à la matrice d'une application linéaire ayant pour noyau le code.

La notion de matrice de contrôle possède à la fois un intérêt théorique dans le cadre de l'étude des codes correcteurs, par exemple pour offrir des critères sur la distance minimale du code ou une condition nécessaire et suffisante pour qu'un code soit parfait et un intérêt pratique pour un décodage efficace.

Sommaire

Contexte

Code correcteur

Article détaillé : Code correcteur.

Un code correcteur possède pour objectif la détection ou la correction d'erreurs après la transmission d'un message. Cette correction est permise grâce à l'ajout d'informations redondantes. Le message est plongé dans un ensemble plus grand, la différence de taille contient la redondance, l'image du message par le plongement est transmis. En cas d'altération du message, la redondance est conçue pour détecter ou corriger les erreurs. Un exemple simple est celui du code de répétition, le message est, par exemple, envoyé trois fois, le décodage se fait par vote. Ici, l'ensemble plus grand est de dimension triple à celle du message initial.

Rappelons les éléments de base de la formalisation. Il existe un ensemble E constitué de suites à valeurs dans un alphabet et de longueur k, c’est-à-dire qu'à partir du rang k, toutes les valeurs de la suite sont nulles. Ces éléments sont l'espace des messages que l'on souhaite communiquer. Pour munir le message de la redondance souhaitée, il existe une application φ injective de E à valeurs dans F, l'espace des suites de longueur n et à valeurs dans un alphabet. La fonction φ est appelée encodage, φ(E) aussi noté C est appelé le code, un élément de φ(E) mot du code, k la longueur du code et n la dimension du code. Ces notations sont utilisées dans tout l'article.

Code linéaire

Article détaillé : Code linéaire.

Un code linéaire dispose d'une structure algébriques plus riche que celle du cadre général des codes correcteurs.

Les alphabets A et A' sont identifiés et munis d'une structure de corps fini. Le cas le plus fréquent consiste à choisir le corps F2 ou l'une de ses extensions finies, on parle alors d'alphabet binaire.

Les ensembles E et F sont naturellement munis d'une structure d'espace vectoriel de dimension respectives k et n. Si Fd désigne le corps fini (cf l'article corps fini) de cardinal d où d est une puissance d'un nombre premier p, alors l'espace vectoriel F est généralement identifié à Fdn.

F est muni d'une distance qui dérive du poids de Hamming. La distance entre deux points de F correspond au nombres de coordonnées non nulles de la différence entre les deux points, dans la base canonique. Un code se décrit par trois paramètres, noté [n, k, δ], n est la dimension du code, k la longueur du code et δ la distance minimale entre deux mots du code. Ces notations sont utilisées dans le reste de l'article.

Enfin, l'application d'encodage φ est choisie linéaire, le code est donc un sous-espace vectoriel.

Définitions

L'objectif d'un code correcteur est la détection ou la correction d'altérations possibles dans la transmission. Dans le cas d'un code linéaire, cette opération est grandement simplifiée. Le code est un sous-espace vectoriel de dimension n - k, il suffit donc de vérifier l'appartenance à ce sous-espace pour déterminer si des altérations se sont produites. Tout espace vectoriel se définit par l'intersection d'autant d'hyperplans que la codimension du sous-espace. Or un hyperplan est le noyau d'une forme linéaire. En conséquence, si F* désigne l'espace dual, on obtient :

\exists (e_i^*) \in {F^*}^{n-k} \quad / \quad x\in \varphi (E) \Leftrightarrow \forall i \in [1, n-k] \quad e_i^*(x) =0

Ce qui s'écrit encore sous forme d'un système d'équations linéaires :

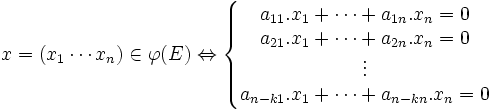
x=(x_1\cdots x_n) \in \varphi (E) \Leftrightarrow \left\{\begin{matrix} a_{11}.x_1+\cdots+a_{1n}.x_n =0\\ a_{21}.x_1+\cdots+a_{2n}.x_n = 0\\ \vdots\\ a_{n-k1}.x_1+\cdots+a_{n-kn}.x_n = 0 \end{matrix}\right.

Ce qui amène à la définition suivante:

  • Une matrice de contrôle d'un code φ(E) est une matrice H de dimension nxn - k tel que :
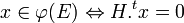
x\in \varphi (E) \Leftrightarrow H.^tx = 0

Ce qui s'exprime encore de la manière suivante :

  • Une matrice de contrôle d'un code φ(E) est une matrice d'une application linéaire surjective de F dans un espace vectoriel ayant pour noyau le code.

On remarque que, comme l'application linéaire est surjective et vérifie l'égalité dim Imφ + dim Kerφ = dim F, l'ensemble d'arrivée de l'application linéaire associée à la matrice de contrôle est un espace vectoriel de dimension n - k.

Exemples

Somme de contrôle binaire

Article détaillé : Somme de contrôle.

La somme de contrôle binaire de longueur k correspond à un code de paramètre [k + 1, k, 2], à un message est associé le mot du code égal au message concaténé avec le bit de parité de la somme de toutes les lettres du message (qui vaut un si la somme est impair et zéro sinon). Il a pour matrice génératrice Gs et, si Ik désigne la matrice unité d'ordre k :

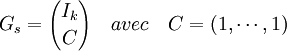
G_s={I_k \choose C}\quad avec \quad C = (1, \cdots ,1)

On remarque que, pour un code binaire, 1 est égal à -1.

Le code est un hyperplan de F, la matrice de contrôle est donc de dimension 1xk, elle correspond à la matrice d'une forme linéaire. Un point de F est un mot du code si et seulement si la somme de ses lettres est paire. Ce qui montre que sa matrice de contrôle Hs possède la forme suivante :

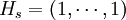
H_s = (1, \cdots ,1)

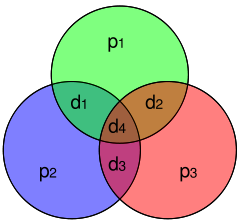
Code de Hamming (7,4)

Article détaillé : Code de Hamming (7,4).
Description du code de Hamming binaire de paramètre [7,4,3]

Le code de Hamming (7,4) est un code binaire de paramètre [7,4,3]. La figure de droite est une représentation graphique de ce code. Le message est le mot d1d2d3d4. Le mot du code est constitué des quatre lettres du mot du message, puis de trois sommes de contrôles p1p2p3. La valeur de pi est égal à zéro si la somme des trois lettres du message incluses dans son cercle sur la figure est paire et un sinon.

Il possède donc la matrice génératrice Gh suivante :

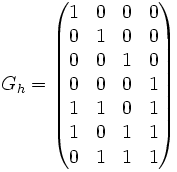
G_h=\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 1 \end{pmatrix}

L'objectif est de trouver trois vecteurs e1*, e2* et e3* de l'espace dual F* libres, qui annulent les quatre vecteurs images de la base de E par φ. Ceci revient, si F* est identifié à F en considérant la base canonique comme une base orthogonale à trouver trois vecteurs orthogonaux aux vecteurs colonnes de la matrice Gh. On obtient par exemple, si Hh désigne une matrice de contrôle :

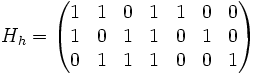
H_h=\begin{pmatrix}1 & 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 1 \end{pmatrix}

Propriétés

Code systématique

Article détaillé : matrice génératrice.

Il existe une forme particulièrement simple pour la matrice génératrice, donné par le code systématique. Dans ce cas, la matrice génératrice prend la forme suivante:

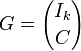
G = {I_k \choose C}

Ou Ik désigne la matrice identité d'ordre k et C une matrice de dimension n-kxk correspondant aux contrôles de redondance.

  • Dans le cas d'un code systématique, et avec les notations précédentes alors l'expression suivante est celle d'une matrice de contrôle :
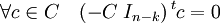
\forall c \in C \quad (-C\;I_{n-k})\,^tc=0

En effet :

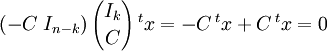
(-C\;I_{n-k})\,{I_k \choose C}\, ^tx= -C\, ^tx + C\, ^tx=0

Cette technique a été appliquée pour déterminer une matrice de contrôle du code de Hamming cité en exemple.

Code parfait

Article détaillé : Code parfait.

La distance minimale δ correspond à la plus petite distance entre deux mots du code, c'est aussi le rayon de la plus grande boule de centre le vecteur nul et ne contenant pas d'autre mot du code que le vecteur nul. Cette distance est importante car elle permet de calculer la valeur t du nombre maximal d'erreurs assurément corrigibles, t est égal au plus grand entier strictement inférieur à δ/2. Elle correspond à la plus grande valeur tel que les boules fermées de centre les points du code et de rayon t ont toutes une intersection vide deux à deux. La matrice de contrôle possède une propriété intéressante, s'exprimant de la manière suivante si la matrice H est identifiée à son application linéaire :

  • La restriction de H à la boule fermée de centre un mot du code et de rayon t est injective.

En effet, considérons deux éléments de la boule, c + e1 et c + e2 où c est un mot du code et e1 et e2 deux vecteurs de poids inférieur ou égal à t. S'ils ont même image par H alors leur différence est élément du code car le code est le noyau de H, donc e1 - e2 est un élément du code. Il est à une distance strictement inférieure à δ du vecteur nul, la boule de centre le vecteur nul et de rayon δ ne rencontre le code qu'au point nul, donc e1 et e2 sont égaux.

Il existe un cas particulier important, celui où les boules fermées de centre les mots du code et de rayon t forment une partition de F, on parle alors de code parfait. La proposition précédente prend la forme suivante :

  • Si le code est parfait, la restriction de H à la boule fermée de centre un mot du code et de rayon t est bijective.

En, effet, Soit h un élément de l'ensemble d'arrivé de H, il admet un antécédent car H est surjective. Cet antécédent est élément d'une boule de la partition. Soit c + e avec c un mot du code et e un élément de F de poids inférieur ou égal à t cet antécédent. Hte admet pour image h car Htc est le vecteur nul (tout mot du code est élément du noyau de H). La restriction de H est donc surjective, elle est injective d'après la proposition précédente.

En plus de permettre le décodage, la matrice de contrôle offre une méthode de calcul de la distance minimale δ :

  • La distance minimale δ d'un code linéaire est égale à la dimension du plus petit sous-espace vectoriel S de F généré par des éléments de la base canonique et tel que la restriction de la matrice de contrôle à S soit non injective.

En effet, soit d la dimension du sous-espace vectoriel S de l'énoncé. Si un mot non nul est de poids strictement inférieur à d, son image par la matrice de contrôle ne peut, par définition de d être nulle, δ est donc supérieure ou égale à d. Réciproquement, il existe un code inclus dans S tel que son image par la matrice est nulle car la matrice de contrôle n'est pas injective sur S. La distance minimale δ est donc inférieure ou égale à d, ce qui termine la démonstration.

Correction d'erreurs

Article détaillé : Décodage par syndrome.

La connaissance des images par H de la boule fermée de centre le vecteur nul et de rayon t permet de corriger les erreurs du message. Si x élément de F est transmis au récepteur, le mot de code le plus proche est x - e où e est l'unique antécédent de Htx dans la boule. Ce qui donne lieu à la définition suivante :

  • Un élément Htx de l'ensemble d'arrivé de H est appelé syndrome.

Si le code est parfait, alors tout vecteur de F s'exprime comme la somme d'un mot du code et d'un vecteur de poids inférieur ou égal à t. Il suffit donc de calculer les images par H de la boule fermée de centre le vecteur nul et de rayon t pour corriger un message contenant t ou moins de t erreurs. Si un message x est reçu, le message corrigé est x - e où e désigne l'antécédent de Htx dans la boule.

Dans le cas où le code n'est pas parfait, une approche similaire est néanmoins possible. Il est nécessaire pour cela de considérer s le plus petit entier tel que les boules fermées de centre les points du code et de rayon s forment un recouvrement de F.

  • La restriction de H à la boule fermée de centre un mot du code et de rayon 's est une surjection.

La démonstration est analogue à la précédente. Dans le cas général la connaissance des antécédents de H dans la boule permet encore le décodage, seulement certains antécédents, (ceux de poids strictement supérieurs à t) ne sont pas uniques, il est alors nécessaire d'en choisir un aléatoirement, le risque de laisser une erreur au décodage voir d'en créer une nouvelle est important.

Notes et références

Articles sur la théorie des codes en rapport avec les codes correcteurs
Code correcteur · Code de répétition · Somme de contrôle · Distance de Hamming · Code parfait et code MDS · Code de Hamming · Code de Hamming (7,4) · Code linéaire · Matrice génératrice · Matrice de contrôle · Décodage par syndrome · Identité de Mac Williams · Code cyclique

Liens externes

Références

  • FJ MacWilliams & JJA Sloane The Theory of Error-Correcting Codes North-Holland, 1977
  • A Spataru Fondements de la Théorie de l'Information Presses Polytechniques Romandes, 1991
  • M. Demazure Cours d'algèbre Cassini, 1997
  • Portail des mathématiques Portail des mathématiques
  • Portail de l’informatique Portail de l’informatique
  • Portail de la sécurité informatique Portail de la sécurité informatique
Ce document provient de « Matrice de contr%C3%B4le ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice De Contrôle de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Matrice de controle — Matrice de contrôle Une matrice de contrôle est un concept de théorie des codes utilisé dans le cas des codes correcteurs linéaires. Elle correspond à la matrice d une application linéaire ayant pour noyau le code. La notion de matrice de… …   Wikipédia en Français

  • Matrice de contrôle — Une matrice de contrôle est un concept de théorie des codes utilisé dans le cas des codes correcteurs linéaires. Elle correspond à la matrice d une application linéaire ayant pour noyau le code. La notion de matrice de contrôle possède à la fois… …   Wikipédia en Français

  • Matrice Génératrice — Une matrice génératrice est un concept de théorie des codes utilisé dans le cas des codes linéaires. Elle correspond à la matrice de l application linéaire de E l espace vectoriel des messages à communiquer dans F, l espace vectoriel contenant… …   Wikipédia en Français

  • Matrice generatrice — Matrice génératrice Une matrice génératrice est un concept de théorie des codes utilisé dans le cas des codes linéaires. Elle correspond à la matrice de l application linéaire de E l espace vectoriel des messages à communiquer dans F, l espace… …   Wikipédia en Français

  • Matrice génératrice — Une matrice génératrice est un concept de théorie des codes utilisé dans le cas des codes linéaires. Elle correspond à la matrice de l application linéaire de E l espace vectoriel des messages à communiquer dans F, l espace vectoriel contenant… …   Wikipédia en Français

  • Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D …   Wikipédia en Français

  • Matrice Inversible — En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In suffit d aprés le… …   Wikipédia en Français

  • Matrice inverse — Matrice inversible En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In… …   Wikipédia en Français

  • Matrice non singulière — Matrice inversible En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In… …   Wikipédia en Français

  • Matrice régulière — Matrice inversible En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”