Matrice Génératrice

Matrice génératrice

Une matrice génératrice est un concept de théorie des codes utilisé dans le cas des codes linéaires.

Elle correspond à la matrice de l'application linéaire de E l'espace vectoriel des messages à communiquer dans F, l'espace vectoriel contenant les codes transmis.

La notion de matrice génératrice possède à la fois un intérêt théorique dans le cadre de l'étude des codes correcteurs, par exemple pour définir la notion de code systématique, et un intérêt pratique pour une implémentation efficace.

Sommaire

1 Contexte
- 1.1 Code correcteur
- 1.2 Code linéaire
2 Définitions
3 Exemples
4 Propriétés
- 4.1 Code systématique
5 Notes et références
- 5.1 Liens externes
- 5.2 Références

Contexte

Code correcteur

Article détaillé : Code correcteur.

Un code correcteur possède pour objectif la détection ou la correction d'erreurs après la transmission d'un message. Cette correction est permise grâce à l'ajout d'informations redondantes. Le message est plongé dans un ensemble plus grand, la différence de taille contient la redondance, l'image du message par le plongement est transmis. En cas d'altération du message, la redondance est conçue pour détecter ou corriger les erreurs. Un exemple simple est celui du code de répétition, le message est, par exemple, envoyé trois fois, le décodage se fait par vote. Ici, l'ensemble plus grand est de dimension triple à celle du message initial.

Rappelons les éléments de base de la formalisation. Il existe un ensemble E constitué de suites à valeurs dans un alphabet et de longueur k, c’est-à-dire qu'à partir du rang k, toutes les valeurs de la suite sont nulles. Ces éléments sont l'espace des messages que l'on souhaite communiquer. Pour munir le message de la redondance souhaitée, il existe une application φ injective de E à valeurs dans F, l'espace des suites de longueur n à valeurs dans un alphabet . La fonction φ est appelée encodage, φ(E) aussi noté C est appelé le code, un élément de φ(E) mot du code, n la longueur du code et k la dimension du code. Ces notations sont utilisées dans tout l'article.

Code linéaire

Article détaillé : Code linéaire.

Un code linéaire dispose d'une structure algébrique plus riche que celle du cadre général des codes correcteurs. Les alphabets A et A' sont identifiés et munis d'une structure de corps fini. Le cas le plus fréquent consiste à choisir le corps F₂ ou l'une de ses extensions finies. Ce corps correspond à l'alphabet binaire dont les tables d'addition et de multiplication sont données ci-dessous:

+	0	1
0	0	1
1	1	0

.	0	1
0	0	0
1	0	1

Les ensembles E et F sont naturellement munis d'une structure d'espace vectoriel de dimension respectives k et n. Si F_d désigne le corps fini (cf l'article corps fini) de cardinal d où d est une puissance d'un nombre premier p, alors l'espace vectoriel F est généralement identifié à F_dⁿ.

F est muni d'une distance qui dérive du poids de Hamming. La distance entre deux points de F correspond au nombres de coordonnées non nulles de la différence entre les deux points, dans la base canonique. Un code se décrit par trois paramètres, noté [n, k, δ], n est la dimension du code, k la longueur du code et δ la distance minimale entre deux mots du code. Ces notations sont utilisées dans le reste de l'article.

Enfin, l'application d'encodage φ est choisie linéaire, le code est donc un sous-espace vectoriel.

Définitions

Une notion naturelle apparait et donne lieu à la définition suivante :

La matrice génératrice G d'un code linéaire est la matrice de l'application linéaire d'encodage φ dans les bases canoniques.

L'égalité suivante est naturellement vérifiée d'après les propriétés des matrices :

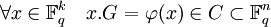
$\forall x \in \mathbb{F}_q^k \quad x.G = \varphi (x) \in C \subset \mathbb{F}_q^n$

On remarque que la dimension de la matrice génératrice est k x n car E est de dimension k et F de dimension n.

Deux matrices génératrices G et G' sont dit équivalentes si et seulement s'il existe une matrice carrée P d'un automorphisme de E tel que : G' = G.P.

Les codes de longueur k et de dimension n sur un même corps fini possèdent exactement les mêmes propriétés si leurs matrices génératrices sont équivalentes. En particulier, ils possèdent la même distance minimale. En effet, l'image de φ, c’est-à-dire le code reste inchangé par toute permutation préalable sur l'ensemble E, en particulier par un automorphisme. Il n'en est pas de même pour F, un automorphisme peut associer à deux vecteurs à une distance de Hamming de δ, deux vecteurs à une distance de un, ce qui détruirait toutes les propriétés du code.

Exemples

Code de répétition

Article détaillé : Code de répétition.

Un code de répétition est un code qui à un message m de longueur k, associe le message m...m. Si son alphabet est choisi comme étant égal à un corps fini, alors le code est linéaire de matrice génératrice G_r égale à :

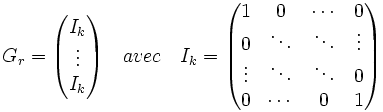
$G_r=\begin{pmatrix} I_k \\ \vdots \\ I_k \end{pmatrix} \quad avec \quad I_k=\begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & 1 \end{pmatrix}$

Somme de contrôle

Article détaillé : Somme de contrôle.

La somme de contrôle correspond à un code de paramètre [k + 1, k, 2], à un message est associé le mot du code égal au message concaténé avec la somme (à valeur dans le corps fini) de toutes les lettres du message. Si le code est binaire, cela revient à associer un si la somme des lettres est impaire et zéro sinon. Dans le cas général, il a pour matrice génératrice G_s et, en utilisant les notations précédentes :

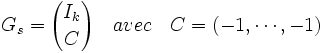
$G_s={I_k \choose C}\quad avec \quad C = (-1, \cdots ,-1)$

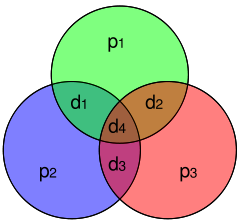
Code de Hamming (7,4)

Article détaillé : Code de Hamming (7,4).

Description du code de Hamming binaire de paramètre [7,4,3]

Le code de Hamming (7,4) est un code binaire de paramètre [7,4,3]. La figure de droite est une représentation graphique de ce code. Le message est le mot d₁d₂d₃d₄. Le mot du code est constitué des quatre lettres du mot du message, puis de trois sommes de contrôles p₁p₂p₃. La valeur de p_i est égal à zéro si la somme des trois lettres du message incluses dans son cercle sur la figure est paire et un sinon.

Il possède donc la matrice génératrice G_h suivante :

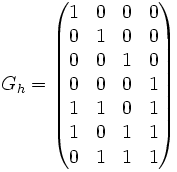
$G_h=\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 1 \end{pmatrix}$

Propriétés

Code systématique

Il existe une forme de la matrice génératrice particulièrement simple, ce qui donne lieu à la définition suivante :

Un code linéaire dont la matrice génératrice possède pour k premières colonnes une matrice identité est dit code systématique.

La matrice prend alors la forme suivante :

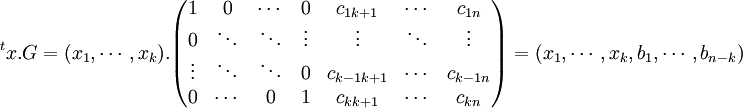
$^tx.G=(x_1,\cdots ,x_k). \begin{pmatrix} 1 & 0 & \cdots & 0 & c_{1 k+1} & \cdots & c_{1 n} \\ 0 & \ddots & \ddots & \vdots & \vdots & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 & c_{k-1 k+1} & \cdots & c_{k-1 n} \\ 0 & \cdots & 0 & 1 & c_{k k+1} & \cdots & c_{k n} \end{pmatrix} =(x_1,\cdots ,x_k,b_1,\cdots ,b_{n-k})$

Cette forme est particulièrement intéressante, le calcul du mot de code consiste à la détermination des n - k dernières coordonnées, car les k premières correspondent à celles du message initiale. De plus, sous réserve d'absence d'altération, le décodage est lui aussi rapide, il consiste à ne considérer uniquement les n premières coordonnées du mot du code. On remarque au passage que le nombre de lignes de la matrice génératrice est égale à l'ordre du vecteur à coder (ici noté k), sans quoi le produit matriciel n'a pas de sens.

Les n - k dernières colonnes (c_ij) de la matrice génératrice sont appelées contrôles de redondance.
Les n - k dernières coordonnées (b_j) d'un code systématique sont dit bits de contrôle ou parfois somme de contrôle.

Ces coordonnées correspondent exactement à la redondance, leur objectif est la détection ou la correction d'erreurs éventuelles. Dans le cas binaire, elles correspondent à la parité de sommes de lettres du message d'origine, on parle alors souvent de bits de parité.

Les codes linéaire peuvent tous se mettre sous cette forme :

Tout code linéaire est équivalent à un code systématique.

Ce qui signifie que, quitte à modifier la base de E, il est possible d'exprimer la matrice génératrice du code grâce à une matrice systématique.

Démonstration

Remarquons tout d'abord qu'il est peut être nécessaire de modifier l'ordre de la base canonique de F. En effet, si par exemple, le code est inclus dans l'espace vectoriel engendré par les n - 1 derniers vecteurs de la base canonique, alors il est vain de chercher une forme systématique sans modifier l'ordre de la base. En revanche, une permutation des vecteurs ne modifie pas la distance de Hamming.

Montrons tout d'abord le lemme suivant:

La plus grande famille de vecteurs de la base canonique engendrant un sous-espace vectoriel d'intersection réduite au vecteur nul avec le code est de cardinal n - k.

C'est une conséquence directe du théorème de la base incomplète. En effet, considérons une base du code, elle forme une famille libre. Le théorème de la base incomplète indique qu'il est possible de compléter cette base par des éléments d'une famille génératrice quelconque, par exemple la base canonique de F. Les vecteurs complétant la famille sont au nombre de n - k car le code est de dimension k et F de dimension n. Ces vecteurs forment une famille répondant aux hypothèses de la proposition. Toute famille de cardinal supérieur possède une codimension supérieure à la dimension du code et donc l'intersection de l'espace généré par une telle famille et le code est non réduit au vecteur nul.

Démontrons alors la proposition:

Tout code linéaire est équivalent à un code systématique.

Soit (f_j) où j est un entier compris entre 1 et n la base canonique de F. Quitte à la réordonner, supposons que les n - k derniers vecteurs engendrent un sous-espace d'intersection réduite au vecteur nul avec le code.

L'objectif est de trouver une base de E (e_i) où i est un entier compris entre 1 et k tel que :

$(ii) \quad \forall i \in [1,k] \; \exists (c_{ji})_{j\in [k+1,n]}\in \mathbb F_d^{n-k} \quad / \quad \varphi (e_i) = f_i + \sum_{j=k+1}^n c_{ji}.f_j$

Soit V_i de F le sous-espace vectoriel engendré par les vecteurs f_j où j est élément de l'union des ensembles {i} et [k + 1, n], où i est choisi élément de [1, k]. V_i contient une intersection non vide avec le code φ(E). En effet, la dimension du code est strictement supérieure à la codimension de V_i. Un élément non nul de cette intersection possède une coordonnée sur f_i non nulle car les n - k derniers vecteurs de la base engendre un sous-espace vectoriel d'intersection réduite au vecteur nul avec le code. Choisissons l'élément de l'intersection ayant une coordonnée égal à 1 sur le vecteur f_i et notons e_i son antécédent par φ. Les k égalités décrites en (ii) sont vérifiées.

Il ne reste plus qu'à montrer que la famille (e_i) est libre. Considérons une relation de dépendance linéaire de cette famille :

$\sum_{i=1}^k \lambda_i.e_i = 0 \quad avec \quad \forall i \in [1, k] \quad \lambda_i \in \mathbb F_d$

L'image par φ de cette relation de dépendance linéaire est encore nulle donc :

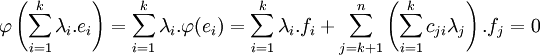
$\varphi \left(\sum_{i=1}^k \lambda_i.e_i \right) = \sum_{i=1}^k \lambda_i.\varphi(e_i) = \sum_{i=1}^k \lambda_i.f_i+ \sum_{j=k+1}^n \left(\sum_{i=1}^k c_{ji}\lambda_j \right).f_j = 0$

Or la famille (f_j) est une base, donc la relation de dépendance linéaire sur cette base est triviale, ce qui démontre la nullité des coefficients λ_i. La famille (e_i) est donc libre, c'est une base car son cardinal est celui de la dimension de E, ce qui termine la démonstration.

Notes et références

Articles sur la théorie des codes en rapport avec les codes correcteurs
Code correcteur · Code de répétition · Somme de contrôle · Distance de Hamming · Code parfait et code MDS · Code de Hamming · Code de Hamming (7,4) · Code linéaire · Matrice génératrice · Matrice de contrôle · Décodage par syndrome · Identité de Mac Williams · Code cyclique

Liens externes

(fr) Code correcteur C.I.R.C par J.P. Zanotti
(fr) L'algèbre et la correction des erreurs par Dany-Jack Mercier Université Antilles-Guyane
(fr) Code Linéaire Université de Bordeaux
(fr) Cours de code par Christine Bachoc Université de Bordeaux
(fr) Code correcteur par M. Coste, A. Paugam, R. Quarez Université de Rennes 1

Références

FJ MacWilliams & NJA Sloane The Theory of Error-Correcting Codes North-Holland, 1977
A Spataru Fondements de la Théorie de l'Information Presses Polytechniques Romandes, 1991
M. Demazure Cours d'algèbre Cassini, 1997

Portail des mathématiques
Portail de l’informatique
Portail de la sécurité informatique

Ce document provient de « Matrice g%C3%A9n%C3%A9ratrice ».

Catégorie : Détection et correction d'erreur

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Matrice Génératrice de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Matrice generatrice — Matrice génératrice Une matrice génératrice est un concept de théorie des codes utilisé dans le cas des codes linéaires. Elle correspond à la matrice de l application linéaire de E l espace vectoriel des messages à communiquer dans F, l espace… … Wikipédia en Français
Matrice génératrice — Une matrice génératrice est un concept de théorie des codes utilisé dans le cas des codes linéaires. Elle correspond à la matrice de l application linéaire de E l espace vectoriel des messages à communiquer dans F, l espace vectoriel contenant… … Wikipédia en Français
Matrice De Contrôle — Une matrice de contrôle est un concept de théorie des codes utilisé dans le cas des codes correcteurs linéaires. Elle correspond à la matrice d une application linéaire ayant pour noyau le code. La notion de matrice de contrôle possède à la fois… … Wikipédia en Français
Matrice de controle — Matrice de contrôle Une matrice de contrôle est un concept de théorie des codes utilisé dans le cas des codes correcteurs linéaires. Elle correspond à la matrice d une application linéaire ayant pour noyau le code. La notion de matrice de… … Wikipédia en Français
Matrice de contrôle — Une matrice de contrôle est un concept de théorie des codes utilisé dans le cas des codes correcteurs linéaires. Elle correspond à la matrice d une application linéaire ayant pour noyau le code. La notion de matrice de contrôle possède à la fois… … Wikipédia en Français
Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D … Wikipédia en Français
Matrice Inversible — En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée A d ordre n est dite inversible ou régulière ou encore non singulière, s il existe une matrice B d ordre n telle que AB = BA = In, ( AB = In suffit d aprés le… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Matrice Génératrice