- Pi
-
Pi[1] est un nombre, que l’on représente par la lettre grecque du même nom : π. C’est le rapport entre la circonférence d’un cercle et son diamètre. On peut également le définir comme le rapport entre la superficie d’un cercle et le carré de son rayon.
Sa valeur approchée arrondie à 10-9 est 3,141592654 en écriture décimale[2],[3].
De nombreuses formules, de physique, d’ingénierie et bien sûr de mathématiques, impliquent π, qui est une des constantes les plus importantes des mathématiques[4].
Le nombre π est irrationnel, c’est-à-dire qu’on ne peut pas l’exprimer comme un rapport de deux nombres entiers ; ceci entraîne que son écriture décimale n’est ni finie, ni périodique. C’est même un nombre transcendant, ce qui signifie qu’il n’existe pas de polynôme non nul à coefficients entiers dont π soit une racine[5].
La détermination d’une valeur approchée suffisamment précise de π, et la compréhension de sa nature sont des enjeux qui ont traversé l’histoire des mathématiques ; la fascination exercée par ce nombre l’a même fait entrer dans la culture populaire.
L’usage de la lettre grecque π, première lettre de « περίμετρος » — périmètre en grec —, n’est apparu qu’au XVIIIe siècle.
Sommaire
Définition et premières propriétés
Définition
Dans les dictionnaires et ouvrages généralistes[6], π est défini comme le rapport constant entre la circonférence d’un cercle et son diamètre (forcément dans le plan usuel qui est le plan euclidien). Ce rapport ne dépend pas du cercle choisi, en particulier de sa taille. En effet, tous les cercles sont semblables et pour passer d’un cercle à un autre il suffit de connaître le rapport de la similitude. Par suite, pour tout réel k, si un cercle possède un rayon r (ou un diamètre d = 2r) k fois plus grand qu’un autre, alors son périmètre P sera aussi k fois plus grand ce qui prouve la constance du rapport
 .
.Par ailleurs, cette même similitude multipliera l’aire A par le carré de k, ce qui prouve maintenant que le rapport
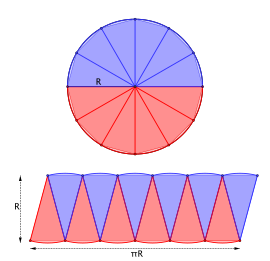
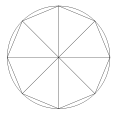
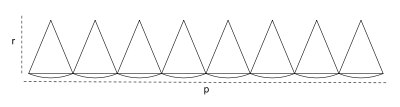
 est constant. On peut montrer[7] que cette constante vaut également π. Le dessin ci-contre illustre ce phénomène : le périmètre du polygone est à peu près 2πr alors qu’en redistribuant les triangles formés on remarque que son aire est à peu près πr2. Pour formaliser le « à peu près » il faudrait faire tendre le nombre de côtés du polygone vers l’infini, ce qui illustre déjà la nature « analytique » de π.
est constant. On peut montrer[7] que cette constante vaut également π. Le dessin ci-contre illustre ce phénomène : le périmètre du polygone est à peu près 2πr alors qu’en redistribuant les triangles formés on remarque que son aire est à peu près πr2. Pour formaliser le « à peu près » il faudrait faire tendre le nombre de côtés du polygone vers l’infini, ce qui illustre déjà la nature « analytique » de π.Il s’avère que cette définition géométrique, la première historiquement et très intuitive, n’est pas la plus directe pour les mathématiciens quand ils veulent définir π en toute rigueur. Les ouvrages plus spécialisés[8] définissent π par l’analyse réelle à l’aide des fonctions trigonométriques elles-mêmes introduites sans référence à la géométrie (voir plus bas).
Définitions alternatives
- Un choix fréquent est de définir π comme le double du plus petit nombre positif x tel que cos(x) = 0[9].
- Une autre définition est envisageable en considérant les propriétés exp(z+w)=exp(z)exp(w) et exp(0)=1 qui découlent de la définition analytique de l’exponentielle et qui font que l’application
 est un morphisme de groupes continu du groupe
est un morphisme de groupes continu du groupe  vers le groupe
vers le groupe  (où
(où  est l’ensemble des complexes de module égal à 1). On démontre alors que l’ensemble des nombres réels t tels que exp(it) = 1 est de la forme
est l’ensemble des complexes de module égal à 1). On démontre alors que l’ensemble des nombres réels t tels que exp(it) = 1 est de la forme  où a est un réel strictement positif. On pose alors π = a / 2[10]. Le calcul intégral permet ensuite de vérifier que cette définition abstraite correspond bien à celle de la géométrie euclidienne.
où a est un réel strictement positif. On pose alors π = a / 2[10]. Le calcul intégral permet ensuite de vérifier que cette définition abstraite correspond bien à celle de la géométrie euclidienne.
- Le groupe Bourbaki propose une définition alternative très voisine en démontrant l’existence d’un morphisme de groupe f continu de
 vers
vers  tel que f(1/4) = i. Il démontre que ce morphisme est périodique de période 1, dérivable et qu’il existe un réel a tel que, pour tout réel x, f'(x) = 2iaf(x). Il définit π comme le réel ainsi trouvé[10].
tel que f(1/4) = i. Il démontre que ce morphisme est périodique de période 1, dérivable et qu’il existe un réel a tel que, pour tout réel x, f'(x) = 2iaf(x). Il définit π comme le réel ainsi trouvé[10].
Les deux méthodes précédentes consistent en réalité à calculer le périmètre du cercle, qu’on a défini par la fonction
 ou la fonction
ou la fonction 
- Mais on peut aussi définir π grâce au calcul intégral en posant :
ce qui revient à calculer l’aire d’un quart de disque de rayon 1.
- Ou bien à l’aide du dénombrement, en appelant
 le nombre de couples d’entiers naturels (k, p) tels que
le nombre de couples d’entiers naturels (k, p) tels que  et en définissant :
et en définissant :
ce qui est une autre méthode pour calculer la surface du quart de disque.
Irrationalité
Le nombre π est irrationnel, ce qui signifie qu’on ne peut pas écrire π=p/q où p et q seraient des nombres entiers. Al-Khawarizmi, au IXe siècle, est persuadé que π est irrationnel[11]. Moïse Maïmonide fait également état de cette idée durant le XIIe siècle. Ce n’est cependant qu’au XVIIIe siècle que Johann Heinrich Lambert prouve ce résultat[12].
C’est en 1761 que ce dernier étudie, dans son ouvrage « Mémoires sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques », le développement en fraction continue de la fonction tangente et montre que le développement en fraction continue de tan(m/n), avec m et n des nombres entiers non nuls, est illimité. Il s’écrit plus précisément[13] :
Or, on sait qu’un nombre dont le développement en fraction continue est illimité est irrationnel, donc quand x est un rationnel non nul, tan(x) est irrationnel. Or, tan(π/4) vaut 1, c’est un rationnel. Par contraposée, on prouve que π/4, et donc π, n’est pas rationnel.
Au cours du XXe siècle, d’autres démonstrations furent trouvées, celles-ci ne demandant pas de connaissances plus avancées que celle du calcul intégral. L’une d’entre elles, due à Ivan Niven, est très largement connue[14],[15]. Une preuve similaire, version simplifiée de celle de Charles Hermite[16],[17], avait été trouvée quelque temps auparavant par Mary Cartwright[18].
Transcendance
π est aussi un nombre transcendant, c’est-à-dire non algébrique : il n’existe pas de polynôme à coefficients rationnels dont π soit une racine[19].
C’est au XIXe siècle que ce résultat est démontré. En 1873, Hermite prouve que la base du logarithme népérien, le nombre e, est transcendant. En 1882, Ferdinand von Lindemann généralise son raisonnement en un théorème (le théorème d’Hermite-Lindemann) qui stipule que, si x est algébrique et différent de zéro, alors ex est transcendant. Or eiπ n’est pas transcendant (puisqu’il est égal à -1). Par contraposée, iπ n’est pas algébrique donc (comme i, lui, est algébrique) π est transcendant.
Une conséquence importante de la transcendance de π est que celui-ci n’est pas constructible. En effet, le théorème de Wantzel énonce en particulier que tout nombre constructible est algébrique. En raison du fait que les coordonnées de tous les points pouvant se construire à la règle et au compas sont des nombres constructibles, la quadrature du cercle est impossible ; autrement dit, il est impossible de construire, uniquement à la règle et au compas, un carré dont la superficie serait égale à celle d’un cercle donné[20].
Représentation décimale
Les 16 premiers chiffres de l’écriture décimale de π sont 3,141 592 653 589 793 (voir les liens externes[2],[3] pour davantage de décimales).
Alors qu’en 2007, on connaît plus de 1012 décimales de π[21], de nombreuses applications n’ont besoin que d’une dizaine de chiffres, comme l’estimation de la circonférence d’un cercle. Par exemple, la représentation décimale de π tronquée à 39 décimales est suffisante pour estimer la circonférence d’un cercle dont les dimensions sont celles de l’univers observable avec une précision comparable à celle du rayon d’un atome d’hydrogène[22],[23].
Étant donné que π est un nombre irrationnel, sa représentation décimale n’est pas périodique et ne prend pas fin. La séquence des décimales de π a toujours fasciné les mathématiciens et les amateurs, et beaucoup d’efforts ont été mis en œuvre afin d’obtenir de plus en plus de décimales et d’en rechercher certaines propriétés[24]. Malgré les importants travaux d’analyse effectués et les calculs qui ont réussi à déterminer plus de 200 milliards de décimales de π, aucun modèle simple n’a été trouvé pour décrire la séquence de ces chiffres[25]. Les chiffres de la représentation décimale de π sont disponibles sur de nombreuses pages web, et il existe des logiciels de calcul des décimales de π qui peuvent en générer des milliards et qu’on peut installer sur un ordinateur personnel.
Par ailleurs, le développement décimal de π ouvre le champ à d’autres questions, notamment celle de savoir si π est un nombre normal, c’est-à-dire que ses chiffres en écriture décimale sont équirépartis. On peut aussi se demander si π est un nombre univers, ce qui signifie qu’on pourrait trouver dans son développement décimal n’importe quelle suite finie de chiffres. En 2006, il n’existait pas de réponse à ces questions[26].
Représentation fractionnaire
Les fractions de nombres entiers suivantes sont utilisées pour mémoriser ou approximer Pi dans des calculs (nombre de chiffres significatifs entre parenthèses) :
Voir ci-dessous pour d’autres approches fractionnaires (Histoire, Approximation numérique, fractions continues et Mémorisation de π).
Approximation de π
On peut trouver une valeur approchée de π de façon empirique, en traçant un cercle, puis en mesurant son diamètre et sa circonférence, puis en divisant la circonférence par le diamètre. Une autre approche géométrique, attribuée à Archimède, consiste à calculer le périmètre Pn d’un polygone régulier à n côtés et à mesurer le diamètre d de son cercle circonscrit, ou celui de son cercle inscrit[27]. Plus le nombre de côtés du polygone est grand, meilleure est la précision obtenue pour la valeur de π.
Archimède a déterminé la précision de cette approche en comparant les résultats obtenus par la formule en utilisant deux polygones réguliers ayant le même nombre de côtés, pour lesquels le cercle est pour l’un circonscrit et pour l’autre inscrit. Il a réussi, avec un polygone à 96 côtés, à déterminer[28] que 3 + 10⁄71 < π < 3 + 1⁄7.
On peut également obtenir des valeurs approchées de π en mettant en œuvre seulement des méthodes purement mathématiques. La plupart des formules utilisées pour calculer π se basent sur ses propriétés mathématiques et demandent pour les comprendre des connaissances en trigonométrie et en calcul intégral. Cependant, certaines sont particulièrement simples, comme la formule de Leibniz[29] :
Cette série converge si lentement que près de 300 termes sont nécessaires pour calculer π à 2 décimales près[30]. Cependant, il est possible de définir une suite similaire qui converge vers π beaucoup plus rapidement, en posant :
et en définissant :
 .
.
Le calcul de π10,10 demande alors un temps similaire à celui requis pour calculer les 150 premiers termes de la série initiale, mais la précision est bien meilleure car
 approche π à 9 décimales près[31]. On trouvera plus loin des méthodes de calcul plus élaborées, donnant des convergences bien plus rapides encore.
approche π à 9 décimales près[31]. On trouvera plus loin des méthodes de calcul plus élaborées, donnant des convergences bien plus rapides encore.Histoire
L’histoire ancienne de π, qu’on peut retracer grâce aux écrits disponibles, suit approximativement l’avancée des mathématiques dans leur ensemble[32]. Certains auteurs divisent l’histoire de π en trois parties : la période antique durant laquelle π a été étudié géométriquement, l’ère classique, aux alentours du XVIIe siècle, où les outils du calcul intégral ont permis des avancées dans la connaissance du nombre π, et la période des ordinateurs numériques[33].
Antiquité
Il semble que, très tôt, les mathématiciens aient été convaincus qu’il existait un rapport constant entre le périmètre du cercle et son diamètre, ainsi qu’entre l’aire du disque et le carré du rayon. Des tablettes babyloniennes datant de 2 000 ans av. J.‑C. et découvertes en 1936[34] présentent des calculs d’aire conduisant à une valeur de π de 3+1/8[35].
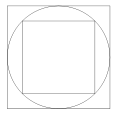
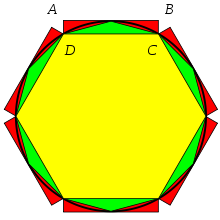
Découvert en 1855, le papyrus de Rhind contient le texte, recopié vers l’an 1650 avant notre ère par le scribe égyptien Ahmès, d’un manuel de problèmes pédagogique plus ancien encore. On y trouve une méthode pour évaluer l’aire d’un disque en prenant le carré dont le côté est égal au diamètre du disque diminué d’un neuvième. Cette méthode conduit à une évaluation de π de 256⁄81. Dans l’illustration ci-contre, le disque a pour diamètre 9. L’aire du disque est légèrement supérieure à l’aire de l’octogone irrégulier obtenu en rognant les coins du carré de côté 9. Cet octogone a pour aire 63, l’aire du disque est alors évaluée à 64 soit l’aire d’un carré de côté 8. Le rapport entre l’aire du disque et le carré du rayon est alors évalué par 64/(9/2)² , c’est-à-dire 256/81.
Le texte indien Shatapatha Brahmana donne à π une valeur de 339/108 ≈ 3,139[réf. nécessaire].
C’est dans le traité d’Archimède (-287, -212) intitulé De la mesure du cercle que l’on peut lire une démonstration liant l’aire du disque et l’aire du triangle ayant pour base le périmètre du cercle et pour hauteur le rayon, démontrant ainsi qu’une même constante apparaît dans le rapport entre aire du disque et carré du rayon et entre périmètre et diamètre[36].
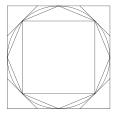
Cette démonstration s’appuie sur la méthode d’exhaustion et un raisonnement par l’absurde. En partant d’un carré inscrit dans le cercle et d’un carré circonscrit au cercle et en multipliant indéfiniment par 2 le nombre de côtés, il prouve que l’aire du disque ne peut être inférieure ni supérieure à celle du triangle correspondant.
Sa démonstration exploite l’idée du découpage en quartiers : le cercle est découpé en plusieurs quartiers qui, mis bout à bout, dessinent des triangles curvilignes de même hauteur. En multipliant le nombre de quartiers, la base des triangles curvilignes est presque droite et la hauteur est proche du rayon, la somme des bases correspond alors au périmètre du cercle et l’aire est alors de 1⁄2 de la base multipliée par la hauteur, c’est-à-dire 1⁄2 du périmètre multiplié par le rayon.
La seconde démonstration consiste à encadrer le périmètre du cercle par le périmètre de polygones réguliers inscrit et circonscrit au cercle et possédant 96 côtés[37]. Pour calculer les périmètres de ces polygones, il part d’hexagones inscrits et circonscrits et met en évidence les formules donnant le périmètre d’un polygone dont le nombre de côtés a doublé. Il démontre ainsi que 3 + 10/71 < π < 3 + 1/7[37]. La moyenne de ces deux valeurs est d’environ 3,14185. Archimède s’arrête à 96 côtés car les calculs qu’il est amené à effectuer, avec valeurs approchées, sont déjà longs pour l’époque. Mais il met en place ainsi une méthode qui sera reprise par ses successeurs et qui peut en théorie être poursuivie indéfiniment. Ptolémée, scientifique grec ayant vécu trois siècles après Archimède, donne une valeur de 3,1416, qu’il a probablement obtenu grâce à Apollonius de Perga[38][réf. insuffisante].
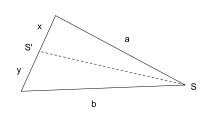
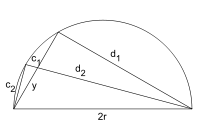
Formules d’ArchimèdeArchimède utilise une propriété liant le pied d’une bissectrice aux côtés adjacents : Dans la figure ci-contre SS′ est la bissectrice de l’angle de sommet S
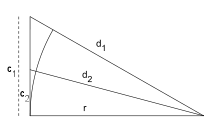
Pour le polygone circonscrit. Dans la figure ci-dessous (gauche), c1 et c2 sont les demi-côtés de deux polygones circonscrits consécutifs. Archimède montre, en utilisant la propriété précédente, que
et réitère 4 fois l’opération à partir de l’hexagone.
Pour le polygone inscrit. Dans la figure ci-contre, c1 et c2 sont les côtés de deux polygones inscrits consécutifs. Archimède montre, en utilisant les triangles semblables et la propriété de la bissectrice queDe nos jours, les formules trigonométriques permettent de simplifier l’algorithme d’Archimède. Les périmètres pi et Pi des polygones inscrits et circonscrits vérifient les relations de récurrence suivantes :
En effet, pour un cercle de rayon 1, si on note an la moitié de l’angle au centre des polygones à l’étape n, on sait que :
et
Si les calculs pratiques peuvent se faire avec une bonne précision en utilisant la valeur 3,14 comme approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au IIIe siècle, en Chine, Liu Hui, commentateur des Neuf chapitres, propose comme rapport entre le périmètre et le diamètre la valeur pratique de 3 mais développe des calculs proches de ceux d’Archimède mais plus performants et fournit une approximation de π de 3,1416[39]. Le mathématicien chinois Zu Chongzhi donne une approximation rationnelle encore plus précise de π[40] : π ≈ 355/113 (dont les développements décimaux sont identiques jusqu’à la 6e décimale, π ≈ 3,1415926 et 355/113 ≈ 3,1415929) et montre que 3,1415926 < π < 3,1415927[41], en utilisant l’algorithme de Liu Hui appliqué à un polygône à 12 288 côtés. Cette valeur demeure la meilleure approximation de π au cours des 900 années qui suivent.
Formules et calculs jusqu’en 1900
Jusqu’en 1400 environ, la précision des approximations de π n’excédait pas les 10 décimales. Les progrès en matière de calcul intégral et de séries vont permettre d’améliorer cette précision. Les séries permettent d’approcher π avec d’autant plus de précision qu’on utilise de termes de la série pour le calcul. Vers 1400, Madhava de Sangamagrama trouve une série permettant de calculer π, la première :
Cette série, qui est en fait un cas particulier de :
 ,
,
est maintenant connue sous le nom de série de Madhava-Leibniz[42],[43] ou série de Gregory-Leibniz depuis que la formule a été redécouverte par James Gregory et Gottfried Wilhelm Leibniz au XVIIe siècle. Malheureusement, la vitesse de convergence de cette série est trop lente pour pouvoir calculer, en pratique, plusieurs décimales : environ 4 000 termes sont nécessaires pour arriver à la précision qu’avait atteint Archimède. Cependant, en transformant la série de la façon suivante :
Madhava a été capable de donner une valeur approchée de π de 3,14159265359, qui a 11 décimales correctes. Le record a été battu en 1424 par le mathématicien perse Al-Kachi, qui a réussi à donner 16 décimales.
La première contribution importante venant d’Europe depuis Archimède a été faite par François Viète, qui en donne douze décimales, avec un encadrement du reste dans son Canon mathématique en 1579. Il est suivi par Adrien Romain, qui donne 15 décimales en 1591, et l’Allemand Ludolph van Ceulen (1540–1610), qui a utilisé la même méthode géométrique afin de donner une estimation de π correcte à 35 décimales près. Il a été si fier de son calcul, qui lui a demandé une grande partie de sa vie, qu’il a fait graver les décimales sur sa pierre tombale[44].
Il est immédiatement suivi par Willebrord Snell, son élève, qui trouve des méthodes plus rapides pour obtenir la même approximation. Dans la même période, les méthodes de calcul intégral et de détermination de séries et produits infinis pour des quantités géométriques ont commencé à émerger en Europe. La première formule de ce type est la formule de Viète :
exposée par François Viète en 1579 dans son Canon mathématique et à nouveau en 1593, dans ses Problèmes variés. Un autre résultat célèbre est le produit de Wallis :
que l’on doit à John Wallis, qui l’a mis en évidence en 1655. Isaac Newton lui-même a utilisé le développement en série de π/6=arcsin 1/2[45] pour calculer 15 décimales de π ; bien plus tard, il a déclaré : « J’ai honte de vous dire combien de décimales j’ai trouvées grâce à ces calculs, n’ayant aucune autre occupation à l’époque. »[46].
En 1706, John Machin a été le premier à trouver 100 décimales de π, en utilisant la formule :
avec :
Les formules de ce type, maintenant connues sous le nom de formules de Machin, ont été utilisées pour battre plusieurs records de décimales connues de π, et demeurent aujourd’hui les formules les plus connues pour calculer π grâce à des ordinateurs. Un record remarquable est détenu par le calculateur prodige Johann Dase qui, en 1844, à l’aide d’une formule de Machin, a calculé de tête 200 décimales de π, à la demande de Gauss. La meilleure valeur obtenue à la fin du XIXe siècle est due à William Shanks (en), qui a passé quinze ans à calculer 707 décimales de π, bien qu’à cause d’une erreur, seules les 527 premières étaient correctes. De nos jours, il est aisé d’éviter de telles erreurs, en faisant faire les calculs par l’ordinateur, et en utilisant deux formules différentes pour éliminer les risques d’erreur de calcul, de programmation, ou du microprocesseur.
Les avancées théoriques du XVIIIe siècle ont amené les mathématiciens à s’interroger sur la nature de π, notamment sur l’absence de motifs périodiques dans ses décimales, une hypothèse raisonnable au vu des calculs numériques, mais pour laquelle il fallait une approche radicalement différente pour la prouver rigoureusement. Ce tour de force a été réalisé par Johann Heinrich Lambert en 1761, qui fut ainsi le premier à prouver l’irrationalité de π, par la suite Adrien-Marie Legendre a aussi prouvé que π² aussi était irrationnel. Cette constante (π²) jouait un rôle notable en mathématique, puisqu’elle apparaissait dans la solution du problème de Bâle, qui consistait à trouver la valeur exacte de
 qui est π²/6 (comme prouvé par Leonhard Euler qui a établi à cette occasion une connexion profonde entre π et les nombres premiers). Dans la foulée, Legendre et Euler ont tous les deux conjecturé que π était un nombre transcendant, ce qui a finalement été prouvé en 1882 par Ferdinand von Lindemann.
qui est π²/6 (comme prouvé par Leonhard Euler qui a établi à cette occasion une connexion profonde entre π et les nombres premiers). Dans la foulée, Legendre et Euler ont tous les deux conjecturé que π était un nombre transcendant, ce qui a finalement été prouvé en 1882 par Ferdinand von Lindemann.Origine de la notation
C’est au cours du XVIIIe siècle que s’établit l’usage de la lettre grecque « π »[47], première lettre des mots grecs περιφέρεια (périphérie) et περίμετρος (périmètre, c’est-à-dire circonférence) pour le rapport de la circonférence du cercle sur son diamètre.
À partir du XVIIe siècle certains mathématiciens utilisent la notation π/δ où π désigne la circonférence et δ le diamètre[48]. Le premier à utiliser simplement π est William Jones[47] dans son livre Synopsis palmariorum mathesios publié en 1706, à propos du calcul astucieux de ce nombre par la série de son ami Machin. Les mathématiciens continuent cependant d’utiliser d’autres notations. Parmi ceux-ci Euler se met à la notation de Jones[49] dans sa correspondance à partir de 1736. Il l’adopte dans son livre Introductio in analysin infinitorum publié en 1748, ce qui eut certainement une grande influence. La notation finit par s’imposer vers la fin du XVIIIe siècle[50].
Ère informatique
Alors que quelques dizaines de décimales de π sont largement suffisantes pour les calculs pratiques qu’effectue un physicien, la conquête des décimales du nombre π n’a pas cessé avec l’arrivée des ordinateurs, qui ont permis de calculer un très grand nombre de ces décimales.
En 1949, à l’aide de l’ENIAC, John von Neumann a obtenu 2037 décimales de π, suite à un calcul qui a duré 70 heures[51],[52]. Des milliers de décimales supplémentaires ont été trouvées au cours des décennies suivantes, l’étape du million de chiffres ayant été passée en 1973. Les progrès n’ont pas seulement été dus aux ordinateurs de plus en plus rapides, mais aussi aux nouveaux algorithmes utilisés. L’une des avancées les plus significatives a été la découverte de la transformée de Fourier rapide dans les années 1960, qui a permis aux ordinateurs de manipuler rapidement de très grands nombres.
Au début du XXe siècle, le mathématicien indien Srinivasa Ramanujan a trouvé de nombreuses nouvelles formules faisant intervenir π ; certaines d’entre elles sont remarquables par leur élégance et leur profondeur mathématique[53]. L’une de ces formules est la série suivante :
La formule ci-dessous, possédant un lien étroit avec celle énoncée ci-dessus, a été découverte par David et Gregory Chudnovsky en 1987 :
Cette formule donne 14 nouvelles décimales de π à chaque terme[53]. Vers la fin des années 1980, les frères Chudnovsky l’ont utilisée pour battre plusieurs records de décimales de π calculées. Elle demeure la formule la plus utilisée pour calculer π sur des ordinateurs personnels.
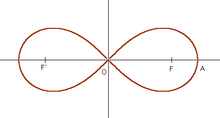
Alors que les séries permettent d’obtenir des valeurs approchées de π avec un taux de précision supplémentaire à chaque terme qui est constant, il existe des algorithmes itératifs qui multiplient le nombre de décimales correctes à chaque étape, avec cependant l’inconvénient que chaque étape demande généralement un calcul « coûteux ». Une grande avancée a eu lieu en 1975 lorsque Richard Brent et Eugene Salamin ont découvert indépendamment l’algorithme Salamin-Brent, qui double le nombre de décimales correctes à chaque étape[54]. Il s’appuie sur un vieux résultat pressenti puis démontré par Gauss. En 1818, celui-ci démontre le lien existant entre la moyenne arithmético-géométrique de 1 et √2 (M(1,√2)), la longueur de la lemniscate de Bernoulli et π. La longueur de la lemniscate est
 où r représente la distance OA entre le centre et un sommet de la lemniscate et où
où r représente la distance OA entre le centre et un sommet de la lemniscate et où  est la constante de la lemniscate. Si on note G, la constante de Gauss, c’est-à-dire l’inverse de M(1,√2) alors :
est la constante de la lemniscate. Si on note G, la constante de Gauss, c’est-à-dire l’inverse de M(1,√2) alors :Salamin et Brent ont utilisé ce résultat pour construire l’algorithme qui porte leur nom, et grâce auquel la conquête des décimales de π va alors avancer conjointement avec celle des décimales de √2[55].
L’algorithme consiste à poser :
 ,
,
puis à définir les relations de récurrence suivantes :
et enfin à calculer ces termes jusqu’à ce que an et bn soient assez proches. On a alors une valeur approchée de π donnée par :
En utilisant cet algorithme, seuls 25 termes sont nécessaires pour calculer 45 millions de décimales. Un algorithme similaire qui quadruple la précision à chaque étape a été trouvé par Jonathan et Peter Borwein[56]. C’est grâce à ces méthodes qu’en 1999, Yasumasa Kanada et son équipe ont battu le record du nombre de décimales de π qui datait de 1980, en atteignant les 206 158 430 000 chiffres.
En août 2010, le record est à nouveau battu par deux informaticiens (un japonais et un américain) avec 5 000 milliards de décimales[57].
En 1997, la formule BBP, découverte par Simon Plouffe, a fait de nouveau progresser la connaissance de π[58]. La formule,
est remarquable car elle permet de calculer n’importe quel chiffre de l’écriture de π en base hexadécimale ou binaire, sans calculer les précédents[58]. Entre 1998 et 2000, le projet de calcul distribué PiHex a utilisé une variante de la formule BBP due à Fabrice Bellard pour calculer le 1 000 000 000 000 000e chiffre en binaire de π, qui s’est révélé être 0[59].
Si une formule de la forme :
était trouvée, avec b et c des entiers positifs et p et q des polynômes de degrés fixés à coefficients entiers (comme pour la formule BBP ci-dessus), ce serait l’un des moyens les plus efficaces pour calculer n’importe quel chiffre dans l’écriture de π en base bc sans avoir à calculer les précédents, en un temps dépendant uniquement du nombre de termes de la série calculé et du degré des polynômes.
En 2006, Simon Plouffe a trouvé plusieurs formules faisant intervenir π[60]. En posant q = eπ (constante de Gelfond), on a :
ainsi que :
où k est un nombre impair, et a, b, c sont des nombres rationnels.
Utilisation en mathématiques et en sciences
Géométrie
π apparaît dans de nombreuses formules de géométrie impliquant les cercles et les sphères :
Forme géométrique Formule Circonférence d’un cercle de rayon r et de diamètre d 
Aire d’un disque de rayon r 
Aire d’une ellipse de demi-axes a et b 
Volume d’une boule de rayon r 
Aire surfacique d’une sphère de rayon r 
Volume d’un cylindre de hauteur h et de rayon r 
Aire surfacique d’un cylindre de hauteur h et de rayon r 
Volume d’un cône de hauteur h et de rayon r 
Aire surfacique d’un cône de hauteur h et de rayon r 
π se retrouve aussi dans le calcul des surfaces et volumes des hypersphères (à plus de trois dimensions).
Nombres complexes
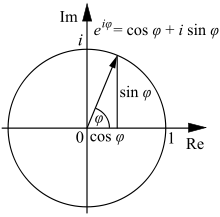 La formule d’Euler illustrée dans le plan complexe. Une augmentation de l’angle φ de π radians (180°) donne l’identité d’Euler.
La formule d’Euler illustrée dans le plan complexe. Une augmentation de l’angle φ de π radians (180°) donne l’identité d’Euler.
Un nombre complexe z peut s’exprimer en coordonnées polaires de la façon suivante :
L’apparition fréquente de π en analyse complexe a pour origine le comportement de la fonction exponentielle complexe, décrite par la formule d’Euler
où i est l’unité imaginaire satisfaisant la relation i2 = −1 et e ≈ 2.71828 est la constante de Néper. Cette formule implique que les puissances imaginaires de e décrivent des rotations sur le cercle unité du plan complexe ; ces rotations ont une période de 360°=2π. En particulier, une rotation de 180°=π donne l’identité d’Euler
 et donc
et donc 
Cette formule a été qualifiée de « formule la plus remarquable des mathématiques » par Richard Feynman, car elle réunit en seulement 7 caractères l’addition, la multiplication, l’exponentiation, l’égalité et les constantes remarquables 0, 1, e, i et π[61].
Suites et séries
De nombreuses suites ou séries convergent vers π ou un multiple rationnel de π et sont même à l’origine de calculs de valeurs approchées de ce nombre.
Méthode d’Archimède
 .
.
Les deux suites définies par
 , et
, et  , n ≥ 3, représentent les demi-périmètres des polygones réguliers à n côtés, inscrit dans le cercle trigonométrique pour sn, exinscrit pour tn. On les exploite par des suites extraites dont l’indice (le nombre de côtés du polygone) double à chaque itération, pour obtenir π par passage à la limite d’expressions utilisant les opérations arithmétiques élémentaires et la racine carrée. Ainsi, on peut s’inspirer de la méthode utilisée par Archimède — voir historique du calcul de π — pour donner une définition par récurrence des suites extraites de termes
, n ≥ 3, représentent les demi-périmètres des polygones réguliers à n côtés, inscrit dans le cercle trigonométrique pour sn, exinscrit pour tn. On les exploite par des suites extraites dont l’indice (le nombre de côtés du polygone) double à chaque itération, pour obtenir π par passage à la limite d’expressions utilisant les opérations arithmétiques élémentaires et la racine carrée. Ainsi, on peut s’inspirer de la méthode utilisée par Archimède — voir historique du calcul de π — pour donner une définition par récurrence des suites extraites de termes  et
et  ou encore
ou encore  et
et  , à l’aide des identités trigonométriques usuelles :
, à l’aide des identités trigonométriques usuelles :En utilisant les identités trigonométriques,
 et
et  (x ∈ [0,π]), on peut exprimer s 2k+1 et s 3×2k (pour k ≥ 1) par emboîtements successifs de racines carrées. On obtient les formules qui suivent pour π.
(x ∈ [0,π]), on peut exprimer s 2k+1 et s 3×2k (pour k ≥ 1) par emboîtements successifs de racines carrées. On obtient les formules qui suivent pour π.π peut alors s’exprimer sous la forme d’une formule où s’emboîtent des racines carrées :
 (k est le nombre de racines carrées emboitées)
(k est le nombre de racines carrées emboitées)
ou encore :
Une autre expression de s2k+1, qui peut se déduire simplement de la première de ces deux égalités (multiplier par √(2+√…)), conduit au produit infini suivant (formule de François Viète, 1593) :
Sommes et produits infinis
 (formule de Leibniz, James Gregory et Madhava de Sangamagrama[62],[63])
(formule de Leibniz, James Gregory et Madhava de Sangamagrama[62],[63])
 (produit de Wallis)
(produit de Wallis)
 (formule due à Ramanujan)
(formule due à Ramanujan)
 (formule due à David et Gregory Chudnovsky)
(formule due à David et Gregory Chudnovsky)
Suites récursives
Suite inspirée de la formule de Brent-Salamin (1975) :
Soient trois suites (An), (Bn) et (Cn) se définissant mutuellement :
on a :
Le nombre de décimales correctes (en base 10) double presque à chaque itération.
Fonction zêta de Riemann
 (Euler)
(Euler)
 ,
,
- et plus généralement, Euler indiqua que ζ(2n) est un multiple rationnel de π2n pour un entier positif n.
Suite logistique
Soit (xn) la suite des itérés de la fonction logistique de paramètre μ = 4 appliquée à un réel x0 choisi dans l’intervalle [0, 1] (c’est-à-dire qu’on définit, pour tout
 ,
,  ). La suite (xn) quitte l’intervalle [0;1] et diverge pour quasiment toutes les valeurs initiales.
). La suite (xn) quitte l’intervalle [0;1] et diverge pour quasiment toutes les valeurs initiales.On a
 pour presque toutes les valeurs initiales x0.
pour presque toutes les valeurs initiales x0.Intégrale
Le nombre π apparait également comme étant le double de la limite du sinus intégral à l’infini :

Probabilités et statistiques
En probabilités et en statistiques, il existe de nombreuses lois qui utilisent la constante π, dont :
- la loi normale d’espérance μ et d’écart type σ, dont la densité de probabilité s’écrit[64] :
- la loi normale de Cauchy, dont la densité de probabilité est[65] :
Les deux formules suivantes, tirées de l’analyse, trouvent des applications pratiques en probabilités. L’une permet de montrer la convergence de la loi binomiale vers la loi de Gauss et l’autre permet de calculer la densité d’une loi de Gauss.
 (formule de Stirling)
(formule de Stirling)
D’autre part, il existe diverses expériences probabilistes où π intervient dans la probabilité théorique. Elles peuvent donc servir, en effectuant un grand nombre d’épreuves, à déterminer une approximation de π.
L’aiguille de Buffon est une expérience de probabilité proposée par Georges-Louis Leclerc, comte de Buffon et consistant à calculer la probabilité qu’une aiguille de longueur a, lancée sur une parquet fait de lattes de largeur L, soit à cheval sur deux lattes, cette probabilité p est[66],[67],[68],[69] :
Cette formule peut être utilisée pour déterminer une valeur approchée de π :

où n est le nombre d’aiguilles lancées, et x celui d’aiguilles qui sont sur deux lattes à la fois.
Cette méthode présente rapidement ses limites ; bien que le résultat soit mathématiquement correct, il ne peut pas être utilisé pour déterminer plus que quelques décimales de π expérimentalement. Pour obtenir seulement une valeur approchée de 3,14, il est nécessaire d’effectuer des millions de lancers[66], et le nombre de lancers nécessaires croît exponentiellement avec le nombre de décimales voulu. De plus, une très faible erreur dans la mesure des longueurs L et a va se répercuter de façon importante sur la valeur trouvée de π. Par exemple, une différence de mesure d’un seul atome sur une aiguille de longueur de 10 centimètres va se retrouver dès la neuvième décimale de π. En pratique, les cas où l’aiguille semble toucher exactement la limite entre deux lattes va accroître l’imprécision de l’expérience, de sorte que les erreurs apparaîtront bien avant la neuvième décimale.
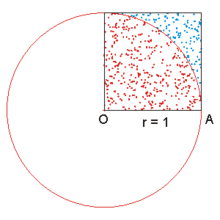
La méthode de Monte Carlo est une autre expérience probabiliste qui consiste à prendre au hasard un point dans un carré de côté 1, la probablité que ce point soit dans le quart de disque de rayon 1 étant de π/4 ; ceci peut facilement se comprendre étant donné que la superficie de ce quart de cercle est π/4 alors que la superficie du carré est 1.
Propriétés avancées
Approximations numériques
Comme π est transcendant, il n’existe pas d’expression d’un nombre qui fasse uniquement appel à des nombres et des fonctions algébriques[19]. Les formules de calcul de π utilisant l’arithmétique élémentaire impliquent généralement les sommes infinies. Ces formules permettent d’approximer π avec le moins d’erreur que l’on désire[70], sachant que plus on rajoute de termes dans le calcul, plus le résultat sera proche de π.
Par conséquent, les calculs numériques doivent utiliser des approximations de π. Dans de nombreux cas, les approximations 3,14 ou 22/7 suffisent, bien que les ingénieurs utilisent souvent 3,1416 (5 chiffres significatifs) ou 3,14159 (6 chiffres significatifs) pour plus de précision. Les approximations 22/7 et 355/113, avec respectivement 3 et 7 chiffres significatifs, sont obtenus à partir de l’écriture en fraction continue de π.
L’approximation de π en 355/113 est la meilleure qui puisse être exprimée avec uniquement 3 chiffres au numérateur et au dénominateur, l’approximation 103993/33102 en exige un nombre beaucoup plus important ; ceci venant de l’apparition du nombre élevé 292 dans le développement en fraction continue de π[71].
La première approximation numérique de π fut certainement 3[37]. Dans les cas où une situation ne demande que peu de précision, cette valeur peut servir d’approximation convenable. Si 3 est une estimation par défaut, c’est parce qu’il est le rapport entre le périmètre d’un hexagone régulier inscrit dans un cercle et le diamètre de ce cercle.
Fractions continues
La séquence des dénominateurs partiels du développement en fraction continue de π ne fait apparaître aucun schéma évident[72] :
![\pi=[3;7,15,1,292,1,1,1,2,1,3,1,14,\cdots]](d/d5d6fa8aada5278b6fa120377350810b.png) ,
,
ce qui est une notation équivalente à :
Cependant, il existe des fractions continues généralisées représentant π dont la structure est régulière[73] :
π/2 peut aussi être écrit sous une forme de fraction continue généralisée, faisant intervenir la suite des inverses des nombres entiers :
Questions ouvertes
De nombreuses questions se posent encore : π et e sont deux nombres transcendants mais sont-ils algébriquement indépendants ou bien existe-t-il une équation polynomiale à deux variables et à coefficients entiers dont le couple (π, e) soit une solution ? La question est encore en suspens. En 1929, Alexandre Gelfond prouve que eπ est transcendant[74] et en 1996, Yuri Nesterenko prouve que π et eπ sont algébriquement indépendants.
Comme dit précédemment, on ignore encore si π est un nombre normal, ou même un nombre univers en base 10.
Culture populaire
Sans doute en raison de la simplicité de sa définition, le nombre pi et particulièrement son écriture décimale sont ancrés dans la culture populaire à un degré plus élevé que tout autre objet mathématique[75]. D’ailleurs, la découverte d’un plus grand nombre de décimales de π fait souvent l’objet d’articles dans la presse généraliste, signe que π est un objet familier même à ceux qui ne pratiquent pas les mathématiques[76],[77],[78].
Une tradition anglo-saxonne veut que l’on fête l’anniversaire de π dans certains départements mathématiques des universités le 14 mars. Le 14 mars qui est noté « 3/14 » en notation anglo-saxonne, est donc appelé la journée de pi.
π dans l’art
Nombreux sont les sites ou ouvrages qui signalent la présence du nombre π dans les pyramides et, plus précisément, que π est le rapport entre le périmètre de la base et le double de la hauteur des pyramides[79]. Il est vrai que la pyramide de Khéops possède une pente de 14/11, et que par conséquent, le rapport entre la base et la hauteur est de 22/14. Le rapport 22/7 étant une bonne approximation de π, le rapport entre le périmètre et le double de la hauteur de la pyramide de Khéops est bien voisin de π. Faut-il pour autant y chercher une intention ? Rien n’est moins sûr[80] puisque la pente des pyramides n’est pas constante et que, selon les régions et les époques, on trouve des pentes de 6/5 (pyramide rouge), 4/3 (pyramide de Khephren) ou 7/5 (pyramide rhomboïdale) qui conduisent à un rapport entre périmètre et double de la hauteur éloigné de π.
Il est en tout cas certain que π soit présent dans la culture artistique moderne. Par exemple, dans Contact, un roman de Carl Sagan, pi joue un rôle clé dans le scénario et il est suggéré qu’il y ait un message enfoui profondément dans les décimales de pi, placé par celui qui a créé l’univers. Cette partie de l’histoire a été écartée de l’adaptation cinématographique du roman.
Sur le plan cinématographique, Pi a servi de titre au premier long-métrage de Darren Aronofsky, à qui l’on doit notamment Requiem for a Dream. π est un thriller mathématique sur la découverte de la séquence parfaite, révélant ainsi formule exacte des marchés boursiers de Wall Street ou encore le véritable nom de Dieu.
Dans le registre musical, l’auteur-compositrice-interprète Kate Bush a sorti en 2005 son album Aerial, qui contenait le morceau « π », dont les paroles sont principalement composées des décimales de π[81].
Mémorisation de π
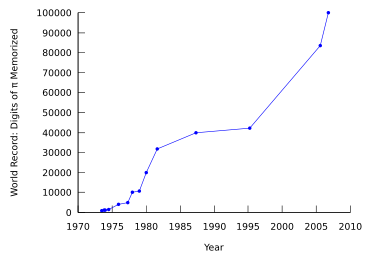
Au delà de la mémorisation de Pi, usuellement ses 3 à 6 premiers chiffres ou par la remarquable valeur approchée de la fraction 355/113 (7 chiffres significatifs), la mémorisation d’un nombre record de décimales de π a longtemps été et demeure une obsession pour de nombreuses personnes. Le 14 mars 2004, à Oxford, le jeune autiste Asperger Daniel Tammet récite (en 5 heures, 9 minutes et 24 secondes) 22 514 décimales. En 2006, Akira Haraguchi, un ingénieur japonais retraité, a réussi à réciter 100 000 décimales de π en 16 heures[82]. Ceci, cependant, n’a pas encore été vérifié par le Livre Guinness des records. Le record de mémorisation de π reconnu par le Guinness des records est de 67 890 chiffres, détenu par Lu Chao, un jeune diplômé chinois[83]. Il lui a fallu 24 heures et 4 minutes pour réciter les 67 890 premières décimales de π sans erreur[84].
Le 17 juin 2009, Andriy Slyusarchuk (en), un neurochirurgien et professeur ukrainien, a affirmé avoir mémorisé 30 millions de décimales de π, qui ont été imprimées en 20 volumes[85]. Bien qu’il n’ait pas récité les 30 millions de chiffres qu’il a dit avoir retenus, certains médias prétendent qu’il était en mesure de réciter dix décimales sélectionnées aléatoirement parmi les volumes imprimés.[réf. souhaitée]
Il y a plusieurs façons de retenir les décimales de π, dont des poèmes dont le nombre de lettres de chaque mot correspond à une décimale, les mots de dix lettres représentant un 0. En voici un exemple[86] :
- Que j’aime à faire apprendre un nombre utile aux sages !
- Immortel Archimède, artiste, ingénieur, (variante : Glorieux Archimède, artiste ingénieux,)
- Qui de ton jugement peut priser la valeur ? (variante : Toi de qui Syracuse aime encore la gloire,)
- Pour moi ton problème eut de pareils avantages. (variante : Soit ton nom conservé par de savants grimoires.)[87]
- Jadis, mystérieux, un problème bloquait
- Tout l’admirable procédé, l’œuvre grandiose
- Que Pythagore découvrit aux anciens Grecs.
- Ô quadrature ! Vieux tourment du philosophe
- Insoluble rondeur, trop longtemps vous avez
- Défié Pythagore et ses imitateurs.
- Comment intégrer l’espace plan circulaire ?
- Former un triangle auquel il équivaudra ?
- Nouvelle invention : Archimède inscrira
- Dedans un hexagone ; appréciera son aire
- Fonction du rayon. Pas trop ne s’y tiendra :
- Dédoublera chaque élément antérieur ;
- Toujours de l’orbe calculée[88] approchera ;
- Définira limite ; enfin, l’arc, le limiteur
- De cet inquiétant cercle, ennemi trop rebelle
- Professeur, enseignez son problème avec zèle
Cette méthode présente ses limites pour la mémorisation d’un très grand nombre de décimales, où il semble plus opportun d’utiliser des méthodes comme la méthode des loci[89],[90].
Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article en anglais intitulé « Pi » (voir la liste des auteurs)
- On l'appelle parfois la constante d’Archimède. C’est en effet cet illustre savant de l’Antiquité grecque qui a fait connaître qu’il s’agissait d’un nombre « compliqué », et qui en a donné des valeurs approchées.
- 128 000 premières décimales de π.
- (en) Site permettant une recherche de chiffres dans les 200 000 000 premières décimales.
- (en) Howard Whitley Eves, An Introduction to the History of Mathematics, Holt, Rinehart & Winston, 1969 [lire en ligne].
- La preuve de ce résultat en 1882 est due à Ferdinand von Lindemann.
- Par exemple le Petit Robert ou le TLFi ; voir Pi (sens B) sur CNRTL.
- (en) Bettina Richmond, « Area of a Circle », Western Kentucky University, 1999.
- Par exemple J. Lelong-Ferrand, J.M. Arnaudiès, cours de mathématiques Tome 2, Dunod Université, 4e édition 1977.
- (en) Walter Rudin, Principles of Mathematical Analysis, McGraw-Hill, 1976 (ISBN 0-07-054235-X), p. 183.
- Histoire du nombre pi. sur Math93.
- (en) Mustafa Mawaldi, Glimpses in the history of a great number: Pi in Arabic mathematics.
- Johann Heinrich Lambert, « Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques », dans Histoire de l'Académie Royale des Sciences et des Belles-Lettres de Berlin, vol. XVII, 1761, p. 265-322 [texte intégral].
- Pour plus de détails voir Fraction continue et approximation diophantienne#Nombre de Pythagore.
- (en) Ivan Niven, « A simple proof that π is irrational », dans Bulletin of the American Mathematical Society, vol. 53, no 6, 1947, p. 509 [texte intégral].
- (en) Helmut Richter, « Pi Is Irrational », Leibniz Rechenzentrum, 1999.
- Charles Hermite, « Extrait d'une lettre de Monsieur Ch. Hermite à Monsieur Paul Gordan », dans Journal für die reine und angewandte Mathematik, vol. 76, 1873, p. 303–311 [texte intégral]
- Charles Hermite, « Extrait d'une lettre de Mr. Ch. Hermite à Mr. Borchardt », dans Journal für die reine und angewandte Mathematik, vol. 76, 1873, p. 342–344 [texte intégral]
- (en) Harold Jeffreys, Scientific Inference, Cambridge University Press, 2011, 3e éd. (ISBN 978-0-52118078-8), p. 268.
- (en) Steve Mayer, « The Transcendence of π ».
- (en) Squaring the Circle, cut-the-knot.
- (en) Current publicized world record of pi.
- (en) Robert M. Young, Excursions in Calculus, Washington, MAA (ISBN 0883853175) [lire en ligne], p. 417.
- (en) Statistical estimation of pi using random vectors.
- (en) Eric W. Weisstein, « Pi Digits », MathWorld.
- (en) Chad Boutin, « Pi seems a good random number generator - but not always the best », dans Purdue University, 2005 [texte intégral].
- Conférence de Jean-Paul Delahaye, le nombre pi est-il simple ou compliqué, mardi 3 octobre 2006, cité des sciences, consultable ici.
- (en) Rick Groleau, « Infinite Secrets: Approximating Pi », NOVA, 2003.
- (en) Petr Beckmann, A History of Pi, Barnes & Noble Publishing, 1989 (ISBN 0880294183).
- (en) Pierre Eymard, The Number π, AMS, février 2004 (ISBN 0821832468) [lire en ligne], p. 53.
- (en) Vito Lampret, « Even from Gregory-Leibniz series π could be computed: an example of how convergence of series can be accelerated », dans Lecturas Mathematicas, 2006 [texte intégral [PDF]].
- Pour plus d’information sur des méthodes analogues, voir Formule d’Euler-Maclaurin.
- (en) Petr Beckmann, A History of π, St. Martin’s Griffin, 1976 (ISBN 0-312-38185-9).
- (en) Archimedes’ constant π. Consulté le 4 novembre 2007.
- Tablettes de Suse - voir par exemple ici
- (en)Otto Neugebauer, the exact sciences in antiquity, p. 47.
- Voir une traduction du texte original
- (en) John J. O’Connor et Edmund F. Robertson, « A history of Pi », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne]..
- (en) C. Boyer, A History of Mathematics, Wiley, p. 168.
- Karine Chemla, Guo Shuchun, Neuf Chapitres. Le Classique de la Chine ancienne et ses commentaires. Édition critique. [détail des éditions], p. 144-147
- Dans son texte Zhui Shu, d’après (en) John J. O’Connor et Edmund F. Robertson, « Zu Chongzhi », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne].
- (en) C. Boyer, A History of Mathematics, Wiley, p. 202.
- (en) George E. Andrews (en), Richard Askey (en) et Ranjan Roy, Special Functions, Cambridge University Press, 1999 (ISBN 978-0-521-78988-2), p. 58.
- (en) R. C. Gupta, On the remainder term in the Madhava-Leibniz’s series, vol. 14, t. 1-4, Ganita Bharati, 1992, p. 68-71.
- (en) Charles Hutton, Mathematical Tables; Containing the Common, Hyperbolic, and Logistic Logarithms …, London: Rivington, 1811 [lire en ligne], p. 13.
- (en) John J. O’Connor et Edmund F. Robertson, « A chronology of Pi », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne]..
- Citation originale : « I am ashamed to tell you to how many figures I carried these computations, having no other business at the time. »
- Florian Cajori, A History of Mathematical Notations [détail des éditions], volume 2, p. 8-13 nos 395 - 398, accessible en ligne.
- non exclusivement, et de plus à des variantes près pour noter le rapport, voir Cajori, ouvrage cité.
- Rien n’indique si c’est sous l’influence de celui-ci ou de son propre chef, cf. Cajori.
- On la trouve par exemple dans Les Élements de géométrie de Legendre, un ouvrage plutôt destiné à un public scolaire, paru en 1794 ; cf. Cajori.
- « An {ENIAC} Determination of pi and e to more than 2000 Decimal Places », Mathematical Tables and Other Aids to Computation, 4 (29), p. 11–15. (janvier 1950).
- « Statistical Treatment of Values of First 2,000 Decimal Digits of e and of pi Calculated on the ENIAC », Mathematical Tables and Other Aids to Computation, 4 (30), p. 109–111, avril 1950
- (en) The constant π: Ramanujan type formulas. Consulté le 4 novembre 2007.
- (en) Richard Brent, Multiple-precision zero-finding methods and the complexity of elementary function evaluation, New York, Analytic Computational Complexity, 1975 [lire en ligne (page consultée le 8 septembre 2007)], p. 151-176.
- La recherche, no 392, Décembre 2005, L’indispensable nombre π.
- (en) Jonathan M. Borwein, Pi: A Source Book, Springer, 2004 (ISBN 0387205713)
- (en) Alexander J. Yee et Shigeru Kondo, 5 Trillion Digits of Pi.
- (en) Bailey, Borwein et Plouffe, « On the Rapid Computation of Various Polylogarithmic Constants », dans Mathematics of Computation, 1997 [texte intégral [PDF]].
- (en) Fabrice Bellard, « A new formula to compute the nth binary digit of pi ». Consulté le 27 octobre 2007.
- (en) Simon Plouffe, « Indentities inspired by Ramanujan’s Notebooks (part 2) ». Consulté le 10 avril 2009.
- (en) Richard Feynman, The Feynman Lectures on Physics: Volume I, juin 1970, p.10 p., « Chapter 22: Algebra ».
- attribuée souvent à Leibniz, mais découverte probablement antérieurement par Gregory, voir (en) John J. O’Connor et Edmund F. Robertson, « A history of Pi », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne].. Cette formule avait également été trouvée vers 1400 par le mathématicien indien Madhava, mais cette découverte resta inconnue du monde occidental.
- (en) John J. O’Connor et Edmund F. Robertson, « Madhava », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne]..
- (en) Eric W. Weisstein, « Gaussian Integral », MathWorld.
- (en) Eric W. Weisstein, « Cauchy Distribution », MathWorld.
- (en) Eric W. Weisstein, « Buffon’s Needle Problem », MathWorld.
- (en) Alex Bogomolny, « Math Surprises: An Example », cut-the-knot, 2001. Consulté le 28 octobre 2007.
- (en) J. F. Ramaley, « Buffon’s Noodle Problem », dans The American Mathematical Monthly, 1969.
- (en) The Monte Carlo algorithm/method sur datastructures, 2007. Consulté le 7 novembre 2007.
- (en) Eric W. Weisstein, « Pi Formulas », MathWorld.
- (en) Xavier Gourdon, « Collection of approximations for π », Numbers, constants and computation. Consulté le 8 novembre 2007.
- suite A001203 de l’OEIS.
- (en) L. J. Lange, An Elegant Continued Fraction for π, vol. 106, t. 5, The American Mathematical Monthly, mai 1999 [lire en ligne], p. 456-458.
- La recherche, no 392, Décembre 2005, L’indispensable nombre π.
- See, e.g, Lennart Berggren, Jonathan M. Borwein, and Peter B. Borwein (eds.), Pi: A Source Book. Springer, 1999 (2nd ed.). ISBN 978-0-387-98946-4.
- (en) E.g., MSNBC, Man recites pi from memory to 83,431 places, 3 juillet 2005, Matt Schudel, Obituaries: "John W. Wrench, Jr.: Mathematician Had a Taste for Pi", The Washington Post, 25 mars 2009, p. B5.
- (en)The Big Question: How close have we come to knowing the precise value of pi? The Independent, 8 janvier 2010.
- (en) Pi, a mathematical story that would take 49,000 years to tell.
- Voir par exemple Le secret de la grande pyramide de George Barbarin.
- Selon The journal of the Society for the study of Egyptian Antiquities, (ISSN 0383-9753), 1978, vol. 8, n4, « la valeur de π apparaissant dans la relation entre la hauteur et la longueur de la pyramide est vraisemblablement co-accidentelle ».
- (en) David Blatner, « UK | Magazine | 3.14 and the rest », BBC News, 2008. Consulté le 2 janvier 2010.
- (en) Tomoko Otake, « How can anyone remember 100,000 numbers? », dans The Japan Times, 2006 [texte intégral].
- (en) Pi World Ranking List. Consulté le 27 octobre 2007.
- (en) « Chinese student breaks Guiness record by reciting 67,890 digits of pi », dans News Guangdong, 2006 [texte intégral].
- (ru)Профессор Андрей Слюсарчук установил мировой рекорд по возможностям человеческой памяти.
- Publié pour la première fois par the academy, d’après la Revue scientifique, 1905. Les quatre premiers vers sont connus en 1846, dans Le livre des singularites, Gabriel Peignot, G. P. Philomneste.
- Pi - Supplément au Petit Archimède no 64-65, Mais 1980, p. 273.
- Le mot orbe est du masculin mais ce ne fut pas toujours le cas, ceci induit à présent une faute d’accord à « calculée » que l’on peut remplacer par « escompté », par exemple, pour conserver le bon nombre de lettres.
- (en) Yicong Liu, « Oh my, memorizing so many digits of pi. », Silver Chips Online, 2004. Consulté le 4 novembre 2007.
- (en) Raz A, Packard MG, Alexander GM, Buhle JT, Zhu H, Yu S, Peterson BS. (2009). A slice of pi : An exploratory neuroimaging study of digit encoding and retrieval in a superior memorist. Neurocase. 6:1-12. DOI:10.1080/13554790902776896 PMID 19585350.
Annexes
Articles connexes
Liens externes
- La preuve par Lambert de l’irrationalité de π (1761), commentée sur le site BibNum
- Nombreuses informations historiques et mathématiques sur pi dans pi314.net
- (en) Le site Wolfram Mathematics compile de nombreuses formules pour π
- (fr) Les décimales de pi [1]
Bibliographie
- Numéro spécial π, Supplément au Petit Archimède, no 64-65, mai 1980
- Jean-Paul Delahaye, Le fascinant nombre π, Éditions Belin, Pour la Science - (ISBN 2-902918-25-9)
- Pierre Eymard, Jean-Pierre Lafon, Autour du nombre Pi, Éditions Hermann, Paris, 1999 - (ISBN 2-7056-1443-5)
- Jörg Arndt & Christoph Haenel : À la poursuite de π, Éditions Vuibert, 2006 - (ISBN 2-7117-7170-9)
- Rheinhold Remmert, « Le nombre π », dans H.-D. Ebbinghaus et al., traduction française et adptation de François Guénard, Les nombres. Leur histoire, leur place et leur rôle de l’Antiquité aux recherches actuelles, Vuibert, (ISBN 2-7117-8901-2)
Wikimedia Foundation. 2010.




















































 ) ·
) ·  ) ·
) ·  ) ·
) ·  ) ·
) ·  ) ·
) ·  )
)
 ) ·
) ·  ) ·
) ·  ) ·
) ·  ) ·
) ·