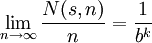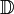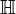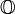Nombre Normal

Nombre Normal

Nombre normal

En mathématiques, un nombre normal est un nombre réel qui a ses chiffres équidistribués dans son développement décimal, ceux-ci apparaissant tous à la même fréquence. Les « chiffres » font référence aux chiffres avant la virgule (la partie entière) et la suite infinie de chiffres après la virgule (la partie fractionnaire).

Supposons b>1 un entier et x un nombre réel. Considérons la suite de chiffres de x dans la base b. Si s est une suite finie de chiffres en base b, nous écrivons N(s,n) pour le nombre d'apparitions de la suite s parmi les n premiers chiffres de x. Le nombre x est appelé normal en base b si

\lim_{n\to\infty} \frac{N(s,n)}{n} = \frac{1}{b^{k}}

pour chaque suite s de longueur k. (Exprimé en mots : la probabilité de trouver la suite s parmi les chiffres de x est précisément celle qui est attendue si la suite de chiffres a été produite complètement de façon aléatoire.) Le nombre x est appelé un nombre normal (ou quelquefois un nombre absolument normal) s'il est normal dans chaque base b.

Le concept fut introduit par le mathématicien français Émile Borel en 1909. En utilisant le lemme de Borel-Cantelli, il démontra le théorème du nombre normal: presque tous les nombres réels sont normaux, dans le sens où l'ensemble des nombres non-normaux possède une mesure de Lebesgue égale à zéro. Ce théorème établit l'existence des nombres normaux, mais Waclaw Sierpinski fut le premier à donner un exemple de l'un d'eux.

L'ensemble des nombres non-normaux n'est pas dénombrable. En effet, il y a une quantité indénombrable de réels qui ne contiennent pas le chiffre 5 dans leur expension décimale, et aucun de ceux-ci n'est normal.

Le nombre de Champernowne

0,1234567891011121314151617...

qui contient dans son développement décimal la concaténation de tous les nombres naturels est normal en base 10, mais il ne l'est pas dans certaines autres bases. De plus c'est un nombre univers en base 10.

La constante de Copeland-Erdős

0,2357111317192329313741...

obtenue en concatenant les nombres premiers est connue comme étant un nombre normal en base 10.

Aucun nombre rationnel n'est normal dans aucune base, puisque la suite de chiffres dans le développement des nombres rationnels est périodique à partir d'un certain rang. Waclaw Sierpinski a fourni la première construction explicite d'un nombre normal en 1917. 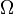Un nombre normal calculable fut construit par Verónica Becher et Santiago Figueira ; un exemple de nombre normal non-calculable est donné par la constante de Chaitin \Omega\,.

Il est extrêmement difficile de démontrer la normalité des nombres qui n'ont pas de construction explicite. Par exemple, on ne sait pas si √2, 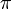\pi\,, ln(2) ou e sont normaux (mais tous sont conjecturés comme normaux, conformément aux expériences). Nous ne savons même pas quels chiffres apparaissent infiniment souvent dans le développement décimal de ces constantes. David H. Bailey et Richard E. Crandall ont conjecturé en 2001 que tout nombre algébrique irrationnel est normal ; bien qu'aucun contre-exemple ne soit connu, on ne connait pas non plus de nombre algébrique qui soit normal dans une base.

Références

  • Bailey, D. H. and Crandall, R. E. « On the Random Character of Fundamental Constant Expansions. » Experimental Mathematics 10, 175-190, 2001. online version
  • Becher, V. and Figueira, S. « An example of a computable absolutely normal number », Theoretical Computer Science, 270, pp. 947-958, 2002.
  • Borel, E. « Les probabilités dénombrables et leurs applications arithmétiques. » Rend. Circ. Mat. Palermo 27, 247-271, 1909.
  • Champernowne, D. G. « The Construction of Decimals Normal in the Scale of Ten. » Journal of the London Mathematical Society 8, 254-260, 1933.
  • Sierpinski, W. « Démonstration élémentaire d'un théorème de M. Borel sur les nombres absolutment normaux et détermination effective d'un tel nombre. » Bull. Soc. Math. France 45, 125-144, 1917.

Voir aussi

Notion de nombre
Ensembles usuels \mathbb{N} Entier naturel • \mathbb{Z} Entier relatif • \mathbb{D} Nombre décimal • \mathbb{Q} Nombre rationnel • \mathbb{R} Nombre réel • \mathbb{C} Nombre complexe Mathématiques
Extensions \mathbb{H} Quaternion • \mathbb{O} Octonion • \mathbb{S} Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • \mathbb{Q}_p Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • i Unité imaginaire • e Constante de Neper • ℵ0 Aleph-zéro • Table de constantes mathématiques
Notions connexes Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif

En informatique, un est un nombre qui est dans un intervalle normal de format en virgule flottante.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre normal ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Normal de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Nombre normal —  Pour l’article homonyme, voir nombre normal (informatique) (en), i.e. nombre qui est dans un intervalle normal de format en virgule flottante.  En mathématiques, un nombre normal est un nombre réel tel que la fréquence d… …   Wikipédia en Français

  • Nombre Ordinal — En linguistique, les mots premier, deuxième, troisième, quatrième, etc. s appellent des adjectifs numéraux ordinaux qui servent à préciser le rang d un objet dans une collection ou l ordre d un événement dans une succession. Cette notion se… …   Wikipédia en Français

  • normal — normal, ale, aux [ nɔrmal, o ] adj. et n. f. • 1753; verbe normal h. XVe; lat. normalis, de norma « équerre » 1 ♦ Math. Droite normale, ou n. f. la normale à une courbe, à une surface en un point : droite perpendiculaire à la tangente, au plan… …   Encyclopédie Universelle

  • Nombre Remarquable — En mathématiques certains nombres se distinguent des autres, jouent un rôle clef, ou apparaissent curieusement dans beaucoup de formules. Ces nombres, considérés comme importants, sont appelés nombres remarquables et portent un nom, qui est… …   Wikipédia en Français

  • Nombre Complexe — Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres… …   Wikipédia en Français

  • Nombre Composé — Un nombre composé est un nombre entier positif qui possède un diviseur positif autre que un ou lui même. Par définition, chaque entier plus grand que un est soit un nombre premier, soit un nombre composé. Les nombres zéro et un ne sont considérés …   Wikipédia en Français

  • Nombre D'or —  Pour l’article homonyme, voir Nombre d or (astronomie).  La proportion définie par a et b est dite d extrême et de moyenne raison lorsque a e …   Wikipédia en Français

  • Nombre Parfait — Un nombre parfait est un nombre entier n strictement supérieur à 1 qui est égal à la somme de ses diviseurs stricts, autrement dit, tel que où σ(n) est la somme des diviseurs entiers positifs de n, n non compris. Le premier nombre parfait est 6,… …   Wikipédia en Français

  • Nombre Premier — 7 est un nombre premier car il admet exactement deux diviseurs positifs …   Wikipédia en Français

  • Nombre Réel — Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs ou nuls,… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”