- Nombre Imaginaire Pur
-
Nombre imaginaire pur
- Cet article est un complément de nombre complexe.
Un nombre imaginaire pur est un nombre complexe qui s'écrit sous la forme ia avec a réel. Par exemple, i, -i et 0 sont des imaginaires purs. Ce sont les nombres complexes dont la partie réelle est nulle. L'ensemble des imaginaires purs est noté
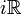 ou
ou 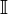 .
.Le carré d'un nombre imaginaire pur est un nombre réel négatif, et les racines carrées d'un nombre réel négatif sont des imaginaires purs. Historiquement, les travaux de Cardan au XVIe siècle ont montré l'intérêt d'utiliser des racines carrées de nombres négatifs dans les calculs. Considérés dans un premier temps comme "imaginaires" ou "inconcevables", ces nombres ont commencé à prendre véritablement un sens autour de 1800.
Sommaire
Définition
L'unité imaginaire est la racine carrée canonique de -1, aujourd'hui le plus souvent notée i en mathématiques. Un imaginaire ou imaginaire pur est un nombre de la forme z=ia où a est un réel. Ce réel est unique et défini par z comme suit : a=-iz. Voici des définitions équivalentes :
- Le nombre iz est un réel,
- Son carré z2 est un nombre réel négatif.
Les racines carrées d'un nombre réel sont soit réels soit imaginaires purs. Les racines carrées d'un nombre réel négatif − a2 (avec a réel) sont les imaginaires purs
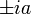 .
.Tout nombre complexe z s'écrit comme somme d'un nombre réel a et d'un nombre imaginaire pur ib. L'écriture z = a + ib est appelée l'écriture cartésienne du nombre complexe z. Les nombres a et b sont respectivement les parties réelle et imaginaire de z. Un imaginaire pur est donc un nombre complexe de partie réelle nulle. Sous forme polaire, un nombre complexe s'écrit z = reiθ. Ce nombre est un imaginaire pur ssi θ vaut π/2, modulo π.
Axe des imaginaires purs
Article détaillé : Plan d'Argand.Le plan d'Argand est une représentation géométrique des nombres complexes par les points d'un plan euclidien. Il comporte deux axes gradués orthogonaux. Le premier axe, horizontal, représente l'axe gradué des réels, et le second axe, vertical, est l'axe des imaginaires purs. Sur ce deuxième axe, l'unité est i.
Un imaginaire pur z correspond alors à un point M de l'axe des imaginaires purs. Plus généralement, le nombre complexe z=a+ib est l'affixe du point M de coordonnées (a,b). Si M et N sont les points d'affixe z et w, alors les droites (OM) et (ON) sont orthogonales ssi le quotient z/w est un imaginaire pur.
Éléments d'histoire
Avant le XVIe siècle, des racines de nombres négatifs apparaissent occasionnellement sur des textes écrits. L'un des plus connus est un calcul de volume réalisé par le mathématicien grec Héron d'Alexandrie, où apparait une racine carrée d'une différence. Malheureusement, ce texte n'est connu que par ses traductions. Il est possible que ce soit une erreur commise par un des traducteurs, hypothèse envisagée par Dominique Flament[1]. On crédite habituellement les travaux de Cardan pour avoir réellement souligné l'importance que peuvent jouer les racines carrées des nombres négatifs dans les calculs. Dans Ars Magma (1545), Jérôme Cardan recherche une méthode pour obtenir une racine carrée réelle d'une équation polynômiale de degré 3. Elle est aujourd'hui connue sous le nom de méthode de Cardan et fait intervenir des extractions de racines carrées de nombres réels, éventuellement négatifs.
Dans Algebra (1572), Raphaël Bombelli s'intéresse à ces racines de nombres négatifs. Les signes pia (plus) et meno (moins) étaient utilisés pour les nombres réels. Bombelli introduit les signes pia di meno (ix...) et mino di mino (-ix...) pour étudier les nombres imaginaires purs. De même qu'un nombre réel strictement positif possède deux racines carrées réelles qui ont des signes opposés, Bombelli reconnaît alors qu'un nombre réel négatif possède deux racines carrées (des nombres "imaginaires") qui viennent avec des signes opposés.
Cependant, il faut attendre le XVIIIe siècle (avec Leibniz, De Moivre et Euler) pour que des calculs plus avancés soient réalisés sur ces nombres, qualifiés d'imaginaires, d'inconcevables ou encore d'inexplicables. Les nombres imaginaires purs sont donc historiquement les premiers nombres complexes étudiés.
Références
- ↑ Dominique Flament, Histoire des nombres complexes
- Portail des mathématiques
Catégories : Propriété numérique | Nombre complexe
Wikimedia Foundation. 2010.