Cercle Inscrit
- Cercle Inscrit
-
Cercle inscrit
En géométrie, un cercle inscrit à un polygone est un cercle qui est tangent à tous les côtés de ce polygone. De manière plus générale, on parle de cercle inscrit dans une surface bornée pour indiquer un cercle de plus grand rayon possible inclus dans la surface.
Existence
Pour qu'un polygone possède un cercle inscrit, il faut que ses bissectrices soient concourantes. Si c'est le cas, le point d'intersection désigne le centre du cercle inscrit. On peut alors trouver le rayon de ce cercle en traçant la perpendiculaire a un segment du cercle et passant par le point d'intersection des bissectrices.
Cas particuliers
Triangle
Tout triangle non plat possède un unique cercle inscrit.
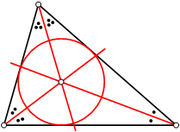
Cercle inscrit dans un triangle
Voir aussi
 Portail de la géométrie
Portail de la géométrie
Catégories : Géométrie du triangle | Cercle et sphère
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Cercle Inscrit de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Cercle inscrit — En géométrie, un cercle inscrit à un polygone est un cercle qui est tangent à tous les côtés de ce polygone. De manière plus générale, on parle de cercle inscrit dans une surface bornée pour indiquer un cercle de plus grand rayon possible inclus… … Wikipédia en Français
Inscrit (géométrie) — Cercle inscrit En géométrie, un cercle inscrit à un polygone est un cercle qui est tangent à tous les côtés de ce polygone. De manière plus générale, on parle de cercle inscrit dans une surface bornée pour indiquer un cercle de plus grand rayon… … Wikipédia en Français
inscrit — inscrit, ite [ ɛ̃skri, it ] adj. et n. • 1835; « écrit » 1532; de inscrire 1 ♦ (Personnes) Dont le nom est inscrit dans la liste constitutive d un groupe. Orateur inscrit. Députés inscrits et non inscrits (à l un des groupes politiques de l… … Encyclopédie Universelle
Cercle Des Neuf Points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… … Wikipédia en Français
Cercle Des Neufs Points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… … Wikipédia en Français
Cercle d'Euler — Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points remarquables… … Wikipédia en Français
Cercle des neuf points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… … Wikipédia en Français
Cercle des neufs points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… … Wikipédia en Français
Cercle Circonscrit — Cercles circonscrits à des triangles En géométrie, un cercle circonscrit à un polygone est un cercle passant par tous les sommets du polygone. Le polygone est alors dit inscrit dans le cercle : on parle de polygone inscriptible. Les sommets… … Wikipédia en Français
Cercle circonscri — Cercle circonscrit Cercles circonscrits à des triangles En géométrie, un cercle circonscrit à un polygone est un cercle passant par tous les sommets du polygone. Le polygone est alors dit inscrit dans le cercle : on parle de polygone… … Wikipédia en Français

