Droite Réelle Achevée
- Droite Réelle Achevée
-
Droite réelle achevée
En mathématiques, la droite réelle achevée désigne l'ensemble 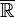 constitué des nombres réels auxquels on adjoint deux éléments notés
constitué des nombres réels auxquels on adjoint deux éléments notés  et
et  (qui ne sont pas considérés comme des nombres réels) vérifiant les propriétés suivantes :
(qui ne sont pas considérés comme des nombres réels) vérifiant les propriétés suivantes :
- pour tout réel x, x <
 ,
,
- pour tout réel x, x >

L'addition et la multiplication définis sur l'ensemble des réels restent valables dans la droite achevée, de sorte que :
- Addition : pour tout réel x,
x + ( ) = (
) = ( )
)
x + ( ) = (
) = ( )
)
( ) + (
) + ( ) = (
) = ( )
)
( ) + (
) + ( ) = (
) = ( )
)
- Multiplication : pour tout réel strictement positif x (x > 0),
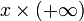 = (
= ( )
)
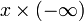 = (
= ( )
)
- pour tout réel strictement négatif x (x < 0),
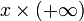 = (
= ( )
)
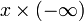 = (
= ( )
)
(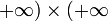 ) = (
) = ( )
)
(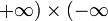 ) = (
) = ( )
)
(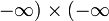 ) = (
) = ( )
)
- en revanche, les expressions
( ) + (
) + ( ),
),
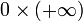 et
et
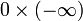 n'ont aucun sens.
n'ont aucun sens.
L'une de ses particularités notables est que tout ensemble inclus dans la droite réelle achevée admet une borne supérieure et une borne inférieure, y compris l'ensemble vide (noté ∅, et qui dans la droite réelle achevée admet  en tant que borne inférieure, et
en tant que borne inférieure, et  en tant que borne supérieure).
en tant que borne supérieure).
Cet ensemble est très utile en analyse, et particulièrement dans certaines théories de l'intégration.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Infini | Espace topologique remarquable | Analyse réelle | Compacité
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Droite Réelle Achevée de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Droite reelle achevee — Droite réelle achevée En mathématiques, la droite réelle achevée désigne l ensemble constitué des nombres réels auxquels on adjoint deux éléments notés et (qui ne sont pas considérés comme des nombres réels) vérifiant les propriétés… … Wikipédia en Français
Droite réelle achevée — En mathématiques, la droite réelle achevée désigne l ensemble constitué des nombres réels auxquels on adjoint deux éléments notés et (qui ne sont pas des nombres). On la note ( la barre symbolise ici le voisinage), [−∞, +∞] ou ∪ {−∞, +∞}. Cet… … Wikipédia en Français
Droite réelle — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… … Wikipédia en Français
Droite Projective — En géométrie, une droite projective est un espace projectif de dimension 1. Un espace vectoriel de dimension 2 y est associé. Plus formellement, une droite projective sur un corps K, dénotée peut être définie comme l ensemble des sous espaces à… … Wikipédia en Français
Droite projective — En géométrie, une droite projective est un espace projectif de dimension 1. En première approche (en oubliant sa structure géométrique), la droite projective sur un corps K, notée , peut être définie comme l ensemble des droites vectorielles du… … Wikipédia en Français
Nombre réel — Pour les articles homonymes, voir Réel. En mathématiques, un nombre réel est un nombre qui peut être représenté par une partie entière et une liste finie ou infinie de décimales. Cette définition s applique donc aux nombres rationnels, dont les… … Wikipédia en Français
Corps des réels — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… … Wikipédia en Français
Ensemble réel — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… … Wikipédia en Français
Nombre Réel — Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs ou nuls,… … Wikipédia en Français
Nombre reel — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… … Wikipédia en Français
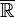 constitué des nombres réels auxquels on adjoint deux éléments notés
constitué des nombres réels auxquels on adjoint deux éléments notés  et
et  (qui ne sont pas considérés comme des nombres réels) vérifiant les propriétés suivantes :
(qui ne sont pas considérés comme des nombres réels) vérifiant les propriétés suivantes : ,
,
 ) = (
) = ( )
) ) = (
) = ( )
) ) + (
) + ( ) = (
) = ( )
) ) + (
) + ( ) = (
) = ( )
)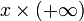 = (
= ( )
)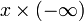 = (
= ( )
)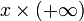 = (
= ( )
)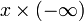 = (
= ( )
)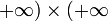 ) = (
) = ( )
)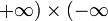 ) = (
) = ( )
)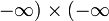 ) = (
) = ( )
) ) + (
) + ( ),
),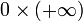 et
et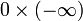 n'ont aucun sens.
n'ont aucun sens. en tant que borne inférieure, et
en tant que borne inférieure, et  en tant que borne supérieure).
en tant que borne supérieure).